Grover keresési algoritmusának elmélete

Ebben a cikkben részletes elméleti magyarázatot talál a Grover-algoritmus működését biztosító matematikai alapelvekről.

A Grover-algoritmus matematikai problémák megoldásához való gyakorlati megvalósításáért lásd: A Grover keresési algoritmusának implementálása.

A probléma leírása

Bármely keresési feladat kifejezhető egy f(x) absztrakt függvénnyel$, amely elfogadja az x$ keresési elemeket$.$ Ha az x$ elem $a keresési feladat megoldása, akkor $f(x)=1$. Ha az x$ elem $nem megoldás, akkor $f(x)=0$. A keresési probléma az f(x_0$$)=1$ x_0 elemek $megkereséséből áll.

A Grover-algoritmus által megoldani kívánt feladat a következőképpen fejezhető ki: egy klasszikus $f(x):\{0,1\}^n \rightnyíl\{0,1\}$, ahol $n$ a keresési terület bitmérete, keresse meg az f(x_0)=1$ bemeneti $x_0$$. Az algoritmus összetettségét az f(x)$ függvény $használatainak száma méri. A legrosszabb esetben $az f(x)$ értéket általában N-1 $$ alkalommal kell kiértékelni, ahol $az N=2^n$ minden lehetőséget kipróbál. Az N-1$ elemek után $az utolsó elemnek kell lennie. A Grover kvantum-algoritmusa sokkal gyorsabban meg tudja oldani ezt a problémát, így a kvadratikus sebesség felgyorsul. A kvadratikus itt azt jelenti, hogy az N-hez$ képest $csak körülbelül $\sqrt{N}$ értékelésre lenne szükség.

Az algoritmus vázlata

Tegyük fel, hogy a $keresési tevékenységhez N=2^n$ jogosult elem tartozik, és ezek indexelhetők úgy, hogy minden egyes elemet 0-tól$$$N-1-ig$ egész számként rendelnek hozzá. Tegyük fel továbbá, hogy vannak $M$ különböző érvényes bemenetek, ami azt jelenti, hogy vannak $olyan M$ bemenetek, amelyekhez $f(x)=1$. Az algoritmus lépései ezután a következők:

1. Kezdje az állapotban $\ket{0}$inicializált n$ qubitek regiszterével$.
2. Készítse elő a regisztert egy egységes szuperpozícióba úgy, hogy h-t alkalmaz $a regiszter minden qubitére: $$|\text{register}\rangle=\frac{1}{\sqrt{N\sum}}_{x=0}^{N-1}|x$\rangle$$
3. Alkalmazza a következő műveleteket a regisztrálási $N_{\text{optimális időpontokra}}$ :
   1. A fázisorákulum $O_f$, amely -1$ feltételes fáziseltolást $alkalmaz a megoldáselemekre.
   2. Alkalmazza $a H-t$ a regiszter minden qubitére.
   3. -1$ feltételes fázisváltás $minden számítási alapállapotra, kivéve$\ket{0}$: . Ezt a -O_0 egységművelet $képviselheti, mivel $O_0$ csak a feltételes fázisra való váltást $\ket{0}$ jelöli.$
   4. Alkalmazza $a H-t$ a regiszter minden qubitére.
4. Mérje meg a regisztert egy nagyon nagy valószínűséggel megoldásnak számító elem indexének lekéréséhez.
5. Ellenőrizze, hogy érvényes-e a megoldás. Ha nem, kezdje újra.

$\text{N_optimal=}\left\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{2}\frac{1}{\right\rfloor$ az iterációk optimális száma, amely a regiszter mérésével maximalizálja a megfelelő tétel beszerzésének valószínűségét.

Megjegyzés

A 3.b, 3.c és 3.d lépés együttes alkalmazását a szakirodalom groveri diffúziós operátoraként ismeri.

A regiszterre alkalmazott általános egységes művelet a következő:

$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{optimal}}}H^{\otimes n}$$

A regiszter állapotának követése lépésről lépésre

A folyamat szemléltetéséhez kövesse a regiszter állapotának matematikai átalakítását egy egyszerű esethez, amelyben csak két qubit van, és az érvényes elem a $\ket{01}.$

1. A regisztráció a következő állapotban kezdődik: $$|\text{register}\rangle=|00\rangle$$

2. Miután minden qubitre alkalmazta $a H-t$, a regiszter állapota a következőre változik: $$|\text{register{1}{\sqrt{=\frac{}\rangle\sum{4}}_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}++\ket{01}\ket{10}+)\ket{11}$$

3. Ezután a rendszer alkalmazza a fázisorákulumot a lekéréshez: $$|\text{regisztrálja=\frac}\ranglea 12(\ket{{00}-\ket{{01}+{10}\ket{+)\ket{{11}$$

4. Ezután $a H$ ismét minden qubiten ad: $$|\text{regisztrálja}\rangle\frac=a 12(\ket{{00}+{01}\ket{-{10}\ket{+)\ket{{11}$$

5. Most a feltételes fázisváltás minden állapotra alkalmazva van, kivéve $\ket{00}$a következőt: $$|\text{12(\ket{{00}-+{10}\ket{\ket{{01}-{11}\ket{) regisztrálása}\rangle=\frac$$

6. Végül az első Grover iteráció a H ismételt alkalmazásával $ér véget a következő lekéréséhez: $$|\text{register$}\rangle=\ket{{01}$$

   A fenti lépések végrehajtásával az érvényes elem egyetlen iterációban található. Ahogy később látni fogja, ez azért van, mert az N=4 és egyetlen érvényes elem esetében $N_\text{optimal}=1$.

Geometriai magyarázat

Annak megtekintéséhez, hogy groveri algoritmus miért működik, vizsgáljuk meg az algoritmust geometriai szemszögből. Legyen $\ket{\text{rossz}}$ az összes olyan állapot szuperpozíciója, amely nem oldja meg a keresési problémát. Tegyük fel, hogy vannak $M$ érvényes megoldások:

$$\ket{\text{rossz}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$

Az állapot $\ket{\text{jó}}$ tulajdonsága az összes olyan állapot szuperpozíciójaként van definiálva, amely megoldást jelent a keresési problémára:

$$\ket{\text{jó}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$

Mivel a jó és a rossz kölcsönösen kizáró készletek, mert egy elem nem lehet érvényes és nem érvényes, a jó}}$ és $\ket{\text{a rossz}}$ állapotok $\ket{\text{ortogonálisak. Mindkét állapot képezi egy sík ortogonális alapját a vektortérben. Ezt a síkot használhatja az algoritmus vizualizációjára.

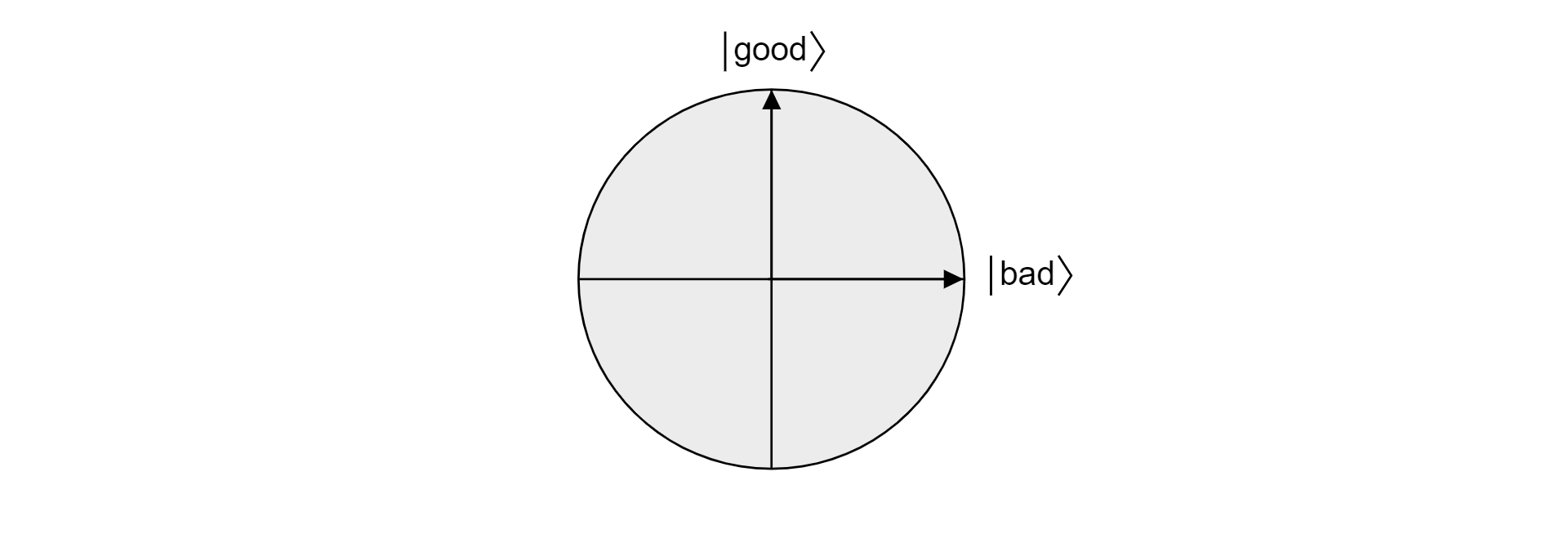
Tegyük fel$\ket{\psi}$, hogy egy tetszőleges állapot, amely a jó}}$ és $\ket{\text{rossz}}$ síkon $\ket{\text{él. Az adott síkban élő állapotok a következőképpen fejezhetők ki:

$$\ket{\psi}=\alpha\ket{\text{jó}} + \beta\ket{\text{rossz}}$$

ahol $\alpha$ és $\beta$ valós számok. Most mutatjuk be a tükröződési operátort $R_{\ket{\psi}}$, ahol $\ket{\psi}$ a síkban élő qubitállapotok vannak. Az operátor a következőképpen van definiálva:

$${\ket{\psi}}=R_2\ket{\psi}\bra{\psi}-\mathcal{I}$$

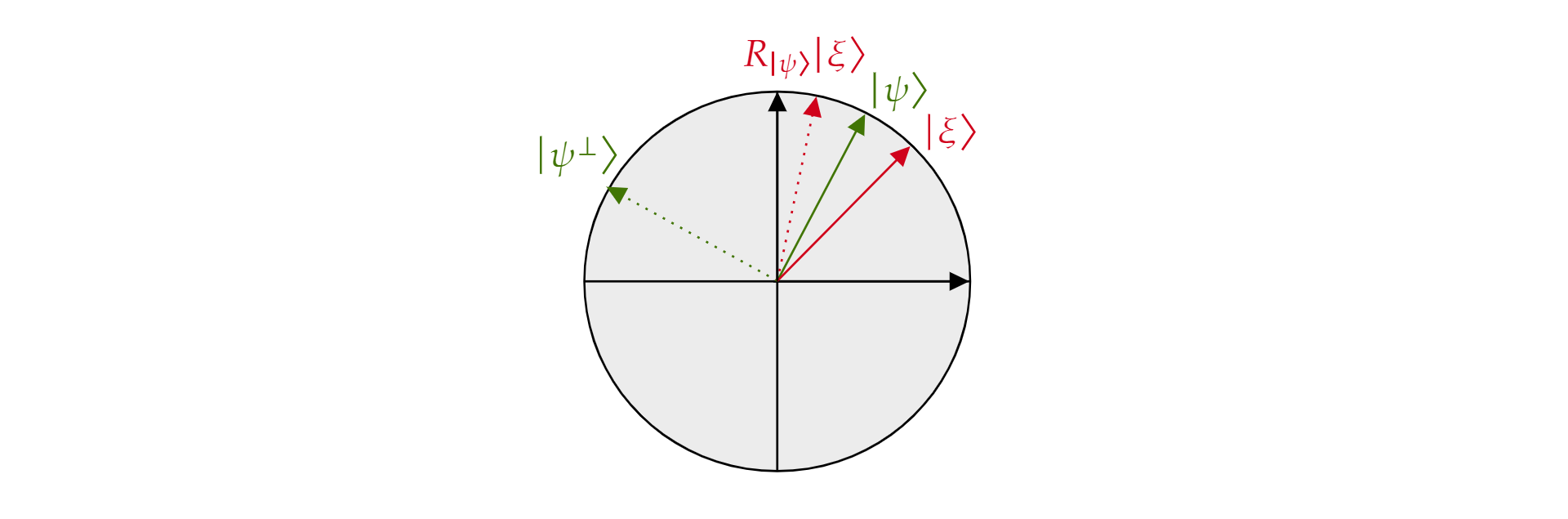
Ez az úgynevezett tükröződési operátor $\ket{\psi}$ , mert geometriailag értelmezhető tükröződésként a irányát $\ket{\psi}$illetően. Ennek megtekintéséhez használja az által létrehozott $\ket{\psi}$ sík ortogonális alapját és annak ortogonális kiegészítését $\ket{\psi(^{\perp}}$). A sík bármely \xi}$ állapota $\ket{felbontható az alábbi módon:

$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$

Ha az operátort $R_{\ket{\psi}}$ a következőre $\ket{alkalmazza: \xi}$:

$${\ket{\psi}}\ket{R_\xi}=\mu \ket{\psi} – \nu {\ket{\psi^{\perp}}}$$

Az operátor $R_\ket{\psi}$ az összetevő ortogonálisát $\ket{\psi}$ invertálja, de az $\ket{\psi}$ összetevőt változatlanul hagyja. $Ezért a R_\ket{\psi}$ a kifejezésre vonatkozó $\ket{\psi}$tükröződés.

Grover algoritmusa a H$ minden qubitre való $első alkalmazása után az összes állapot egységes szuperpozíciójával kezdődik. Ez a következőképpen írható:

$$\ket{\text{minden}}\sqrt{\frac{=M}{N}}\ket{\text{jó}} + \sqrt{\frac{N-M}{N}}\ket{\text{rossz}}$$

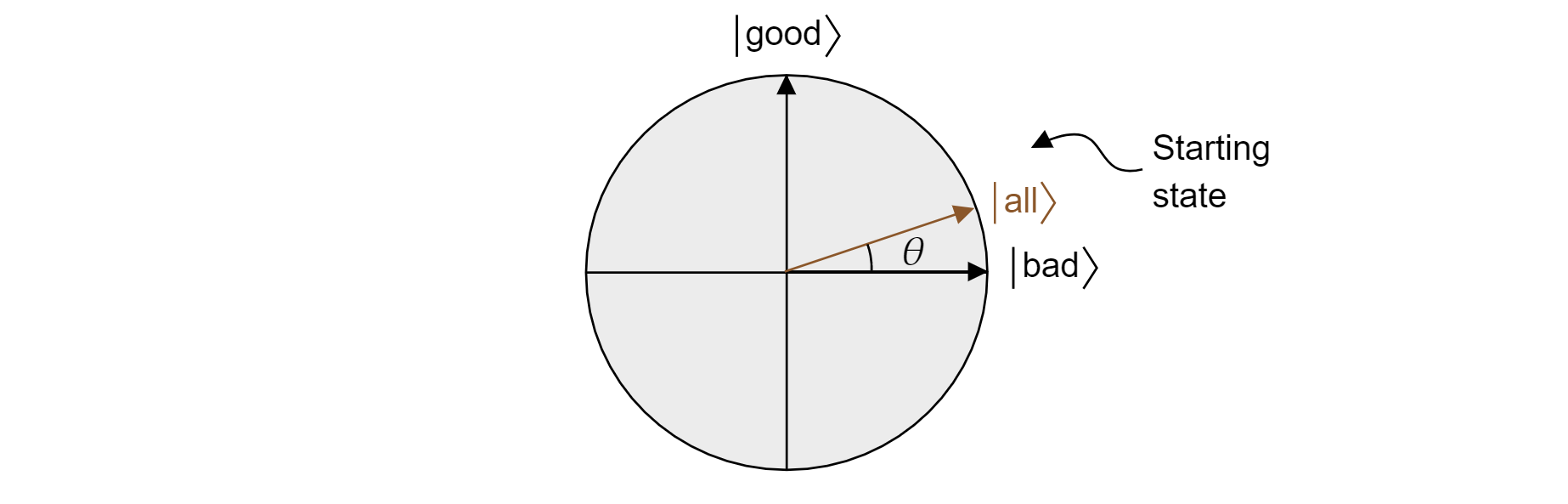
És így az állam a repülőn él. Vegye figyelembe, hogy az egyenlő szuperpozícióból való méréskor a helyes eredmény elérésének valószínűsége csak $|\braket{\text{jó}|{\text{mind}}}|^2=M/N$, ami egy véletlenszerű becsléstől elvárható.

Az oracle $O_f$ negatív fázist ad hozzá a keresési probléma megoldásához. Ezért a rossz}}$ tengely tükröződéseként $\ket{\text{írható:

$$= O_f R_{\ket{\text{bad=}}} 2\ket{\text{rossz}}\bra{\text{}} - \mathcal{I}$$

Hasonlóképpen, a feltételes fázisváltás $O_0$ csak egy fordított tükröződés az állapotról $\ket{0}$:

$$O_0 R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I =}$$

Ennek ismeretében könnyen ellenőrizhető, hogy a -H^{\otimes n O_0 H^{\otimes n}$ groveri diffúziós művelet $is tükrözi-e az állapotot$\ket{}$.} Csak tegye a következőket:

$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n{0}}\ket{0}\bra{H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{mind}}}}\bra{\text{ - \mathcal{I}= R_all{\ket{\text{}}}$$

Kimutatták, hogy Grover algoritmusának minden iterációja két tükröződésből $áll, R_\ket{\text{ és}}$$R_\ket{\text{all}}$.

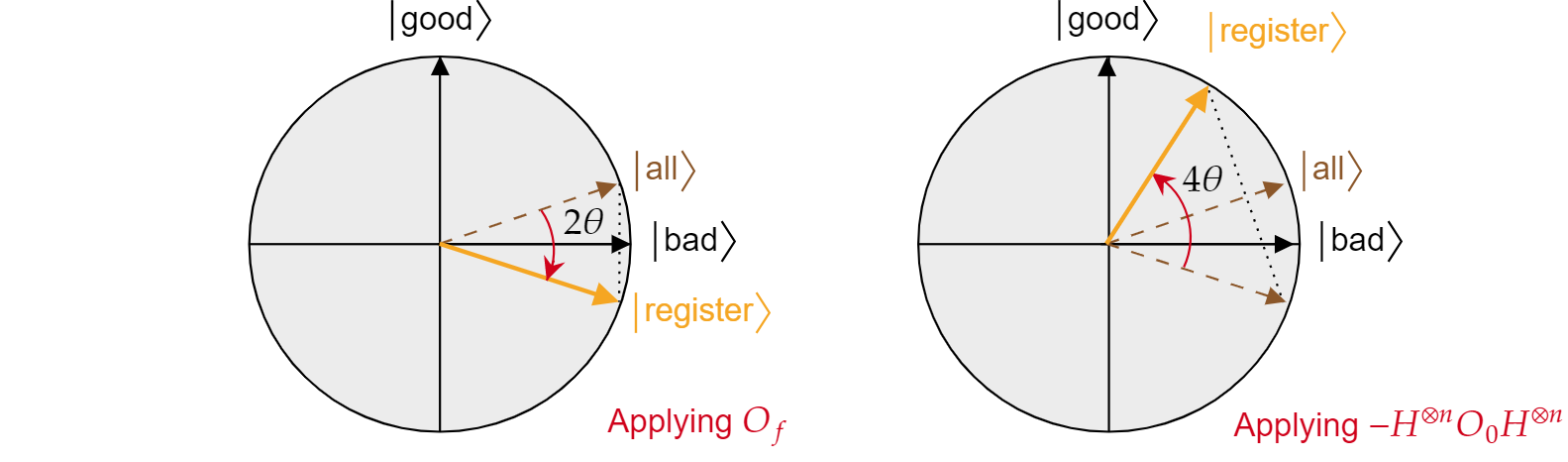
Az egyes Grover iterációk együttes hatása a 2\theta$ szög $óramutató járásával ellentétes irányban történő elforgatása. Szerencsére a szög $\theta$ könnyen megtalálható. Mivel $a \theta$ csak az összes}}$ és $\ket{\text{a rossz}}$ közötti $\ket{\text{szög, a skaláris termék használatával megkeresheti a szöget. Ismert, hogy a $\cos{\theta}=\braket{\text{mind}|\text{rossz}}$, ezért minden}|\text{rosszat}}$ ki kell számítani$\braket{\text{. Az összes}}$ rossz és $\ket{\text{jó}}$ szempontjából}}$$\ket{\text{való felbontásából $\ket{\text{a következő következik:

$$\theta = \arccos{\left(\braket{\text{all}|\text{bad}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$

A regiszter állapota és a $\ket{\text{jó}}$ állapot közötti szög minden iterációval csökken, ami nagyobb valószínűséggel mér érvényes eredményt. A valószínűség kiszámításához egyszerűen ki kell számítania $|\braket{\text{a jó}|\text{regisztert}}|^2$. A jó}}$ és a regiszter$\gamma}}$ (k)$ közötti $\ket{\text{szög jelölése, ahol $k$ az iterációk $\ket{\text{száma:

$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$

Ezért a siker valószínűsége a következő:

$$P(\text{success}) = \cos^2(\gammak)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$

Az iterációk optimális száma

Mivel a sikeresség valószínűsége az iterációk számának függvényeként írható, az iterációk $optimális száma N_{\text{optimális}}$ lehet megtalálni a legkisebb pozitív egész szám számításával, amely (körülbelül) maximalizálja a siker valószínűségi függvényét.

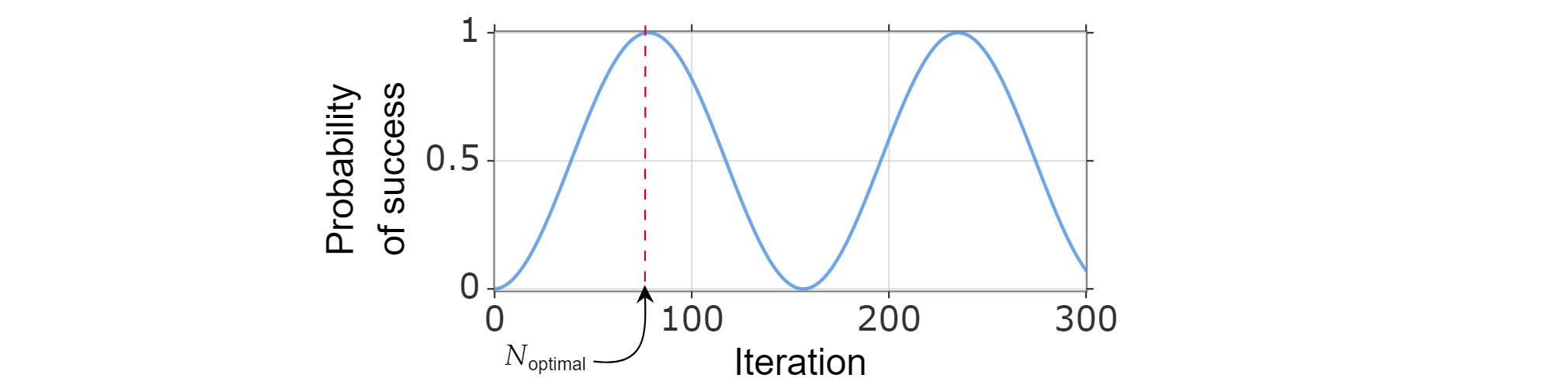
Ismert, hogy a $\sin^2{x}$ eléri az x=\frac{\pi}{2}$ első maximumát$, így:

$$\frac{\pi}{{2}=(2k_{\text{optimal}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$

Ez a következőt nyújtja:

$${\text{k_optimal}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2\frac{= \pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N)}\right$$

Ahol az utolsó lépésben a $\arccos \sqrt{1-x x}=}\sqrt{ + O(x^{3/2}).$

Ezért választhatja $N_\text{optimal}$\lfloor \pi}{{4}\sqrt{\frac{N}{M}}-\right\frac{{1}{2}\rfloor lehetőséget, hogy $N_\text{optimal=\left}\lfloor \frac{$legyen.

Összetettségi elemzés

Az előző elemzésből $az oracle $O_f$ O\left(\sqrt{\frac{N}{M}}\right)$ lekérdezéseire van szükség egy érvényes elem megkereséséhez. Az algoritmus azonban hatékonyan implementálható az idő összetettsége szempontjából? $$ O_0 n biten$$alapuló logikai műveleteken alapul, és ismert, hogy O(n)$ kapukkal $implementálható. A Hadamard kapuknak két rétege $$ is van. Mindkét összetevőnek ezért iterációnként csak $O(n)$ kapura van szüksége. Mivel $N=2^n$, az O(n)=O(log(N))$) következik$. Ezért ha $az O\left(\sqrt{\frac{N}{M}}\right)$ iterációkra és $az iterációnkénti O(log(N))$ kapukra van szükség, a teljes idő összetettsége (az oracle implementációjának figyelembe vétele nélkül) az $O\left(\sqrt{\frac{N}{M}}log(N)\right))$.

Az algoritmus általános összetettsége végső soron az oracle $O_f$ implementációjának összetettségétől függ. Ha egy függvény kiértékelése sokkal bonyolultabb egy kvantumszámítógépen, mint egy klasszikuson, akkor az algoritmus általános futtatókörnyezete hosszabb lesz a kvantumesetben, bár technikailag kevesebb lekérdezést használ.

Hivatkozások

Ha folytatni szeretné a Grover algoritmusának megismerését, az alábbi források bármelyikét ellenőrizheti:

• Eredeti tanulmány: Lov K. Grover
• A Nielsen, M. A. kvantumkeresési algoritmusok szakasza. &Amp; Chuang, I. L. (2010). Kvantumszámítás és kvantuminformációk.
• Grover algoritmusa a Arxiv.org

Következő lépések

• Kvantum köztes reprezentáció
• Vektorok és mátrixok
• T-kapuk és T-gyárak
• Több qubit