Esercitazione: Implementare un generatore quantistico di numeri casuali in Q#

  • Articolo

Nota

Microsoft Quantum Development Kit (QDK classico) non sarà più supportato dopo il 30 giugno 2024. Se si è uno sviluppatore QDK esistente, è consigliabile passare al nuovo azure Quantum Development Kit (QDK moderno) per continuare a sviluppare soluzioni quantistiche. Per altre informazioni, vedere Eseguire la Q# migrazione del codice a QDK moderno.

Informazioni su come scrivere un programma quantistico di base in Q# che sfrutta la natura della meccanica quantistica per produrre un numero casuale.

In questa esercitazione si apprenderà come:

  • Creare un Q# programma.
  • Esaminare i componenti principali di un Q# programma.
  • Definire la logica di un problema.
  • Combinare operazioni classiche e quantistice per risolvere un problema.
  • Usare qubit e sovrapposizioni per creare un generatore quantistico di numeri casuali.

Suggerimento

Per accelerare il percorso di calcolo quantistico, vedere Codice con Azure Quantum, una funzionalità univoca del sito Web di Azure Quantum. In questo caso, è possibile eseguire esempi predefiniti Q# o programmi personalizzati Q# , generare nuovo Q# codice dalle richieste, aprire ed eseguire il codice in VS Code per il Web con un solo clic e porre a Copilot eventuali domande sul calcolo quantistico.

Prerequisiti

Definire il problema

I computer classici non producono numeri casuali, ma piuttosto numeri pseudocasuali. Un generatore di numeri pseudocasuali genera una sequenza deterministica di numeri in base a un valore iniziale, detto seme. Per una migliore approssimazione dei valori casuali, questo seme corrisponde spesso all'ora corrente del clock della CPU.

I computer quantistici, d'altra parte, possono generare numeri veramente casuali. Ciò è dovuto al fatto che la misura di un qubit in sovrapposizione è un processo probabilistico. Il risultato della misurazione è casuale e non è possibile stimare il risultato. Questo è il principio di base dei generatori di numeri casuali quantistici.

Un qubit è un'unità di informazioni quantistica che possono essere in sovrapposizione. Quando viene misurato, un qubit può trovarsi solo nello stato 0 o 1. Tuttavia, prima della misurazione, lo stato del qubit rappresenta la probabilità di leggere un valore 0 o 1 con una misurazione.

Si inizia con un qubit in uno stato di base, ad esempio zero. Il primo passaggio del generatore di numeri casuali consiste nell'usare un'operazione Hadamard per inserire il qubit in una sovrapposizione uguale. La misurazione di questo stato restituisce uno zero o uno con probabilità del 50% di ogni risultato, un bit veramente casuale.

Non è possibile sapere cosa si otterrà dopo la misurazione del qubit in sovrapposizione e il risultato è un valore diverso ogni volta che viene richiamato il codice. Ma come è possibile usare questo comportamento per generare numeri casuali più grandi?

Si supponga di ripetere il processo quattro volte, generando questa sequenza di cifre binarie:

$${0, 1, 1, 0}$$

Se si concatenano, o si combinano, questi bit in una stringa di bit, è possibile formare un numero più grande. In questo esempio, la sequenza di bit ${0110}$ è equivalente a sei in notazione decimale.

$${0110_{\ binary} \equiv 6_{\ decimal}}$$

Se si ripete questo processo molte volte, è possibile combinare più bit per formare qualsiasi numero elevato. Ora è possibile far avere al proprio superiore tale numero come password sicura, perché si può essere certi che nessun hacker spaziale potrà determinare i risultati della sequenza di misurazioni.

Definire la logica del generatore di numeri casuali

Si esamini ora la logica di un generatore di numeri casuali, purché sia disponibile un generatore di bit casuale:

  1. Definire max come il numero massimo da generare.
  2. Definire il numero di bit casuali che è necessario generare. Questa operazione viene eseguita calcolando il numero di bit, nBits, necessari per esprimere numeri interi fino a max.
  3. Generare una stringa di bit casuale con lunghezza pari a nBits.
  4. Se la stringa di bit rappresenta un numero maggiore di max, tornare al passaggio tre.
  5. In caso contrario, il processo è completato. Restituire il numero generato come valore intero.

Impostare ad esempio max su 12. Ciò significa che 12 è il numero massimo che si vuole usare come password sicura.

Per rappresentare un numero compreso tra 0 e 12, sono necessari 4 bit, ovvero ${\lfloor ln(12) / ln(2) + 1 \rfloor}$. Per brevità, non viene descritto come derivare questa equazione.

Si supponga di generare la stringa di bit ${1101_{\ binary}}$, equivalente a ${13_{\ decimal}}$. Poiché 13 è maggiore di 12, si ripete il processo.

Si genera quindi la stringa di bit ${0110_{\ binary}}$, equivalente a ${6_{\ decimal}}$. Poiché 6 è minore di 12, il processo è completato.

Il generatore di numeri casuali quantistici restituirà il numero 6 come password. Nella pratica impostare un numero più grande come massimo perché è possibile violare facilmente i numeri più piccoli semplicemente provando tutte le password possibili. Infatti, perché risulti più difficile indovinare o violare la password, è possibile usare il codice ASCII per convertire i dati binari in testo e generare una password usando numeri, simboli e lettere maiuscole/minuscole.

Scrivere un generatore di bit casuale

Il primo passaggio consiste nel scrivere un'operazione Q# che genera un bit casuale. Questa operazione sarà uno dei blocchi predefiniti del generatore di numeri casuali.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Osservare il nuovo codice.

  • Viene definita l'operazione GenerateRandomBit, che non accetta input e produce un valore di tipo Result. Il tipo Result rappresenta il risultato di una misurazione e può avere due valori: Zero o One.
  • Allocare un singolo qubit con la use parola chiave . Quando viene allocato, un qubit si trova sempre nello stato Zero.
  • Usare l'operazione H per inserire il qubit in una sovrapposizione uguale.
  • Usare l'operazione M per misurare il qubit, restituire il valore misurato (Zero o One).
  • Usare l'operazione Reset per reimpostare il qubit sullo stato |0〉.

Inserendo il qubit in sovrapposizione con l'operazione H e misurandolo con l'operazione M, il risultato è un valore diverso ogni volta che viene richiamato il codice.

Visualizzare il Q# codice con la sfera Bloch

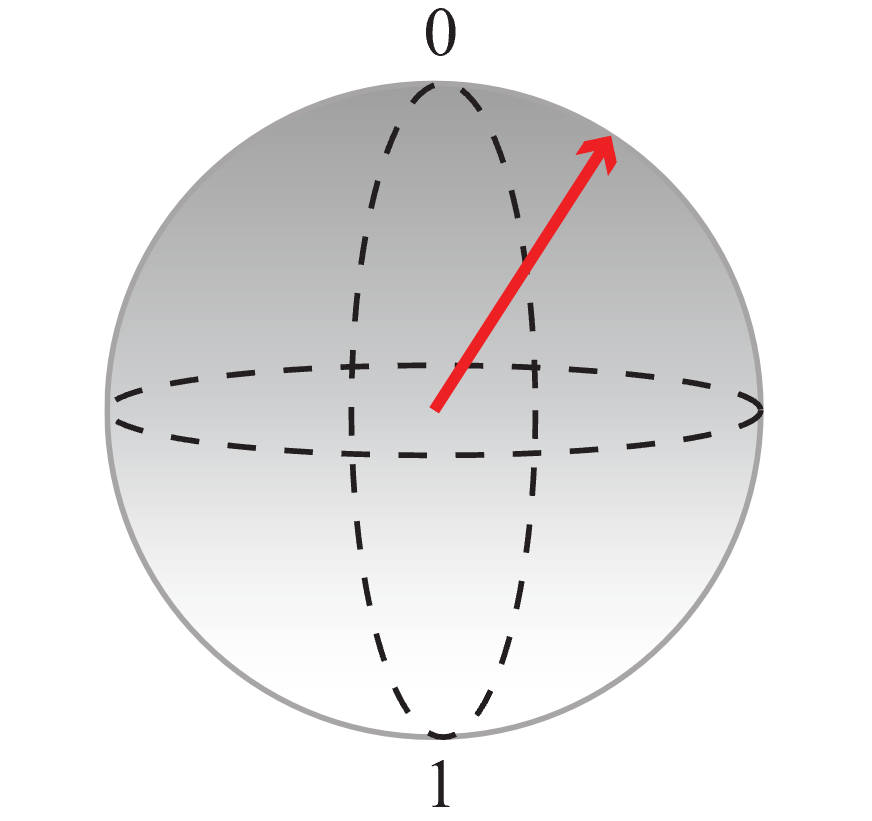
Nella sfera di Bloch il polo nord rappresenta il valore classico 0 e il polo sud rappresenta il valore classico 1. Qualsiasi sovrapposizione può essere rappresentata da un punto sulla sfera (rappresentato da una freccia). Più vicina è la fine della freccia a un polo, più alta è la probabilità che il qubit collassi nel valore classico assegnato a tale polo quando viene misurato. Ad esempio, lo stato del qubit rappresentato dalla freccia rossa nella figura seguente ha una probabilità più elevata di restituire il valore 0 se lo si misura.

Diagramma che mostra uno stato qubit con una probabilità elevata di misurazione dello zero.

È possibile usare questa rappresentazione per visualizzare le operazioni eseguite dal codice:

  1. Iniziare con un qubit inizializzato nello stato 0 e applicare un'operazione H per creare una sovrapposizione uguale in cui le probabilità di 0 e 1 siano le stesse.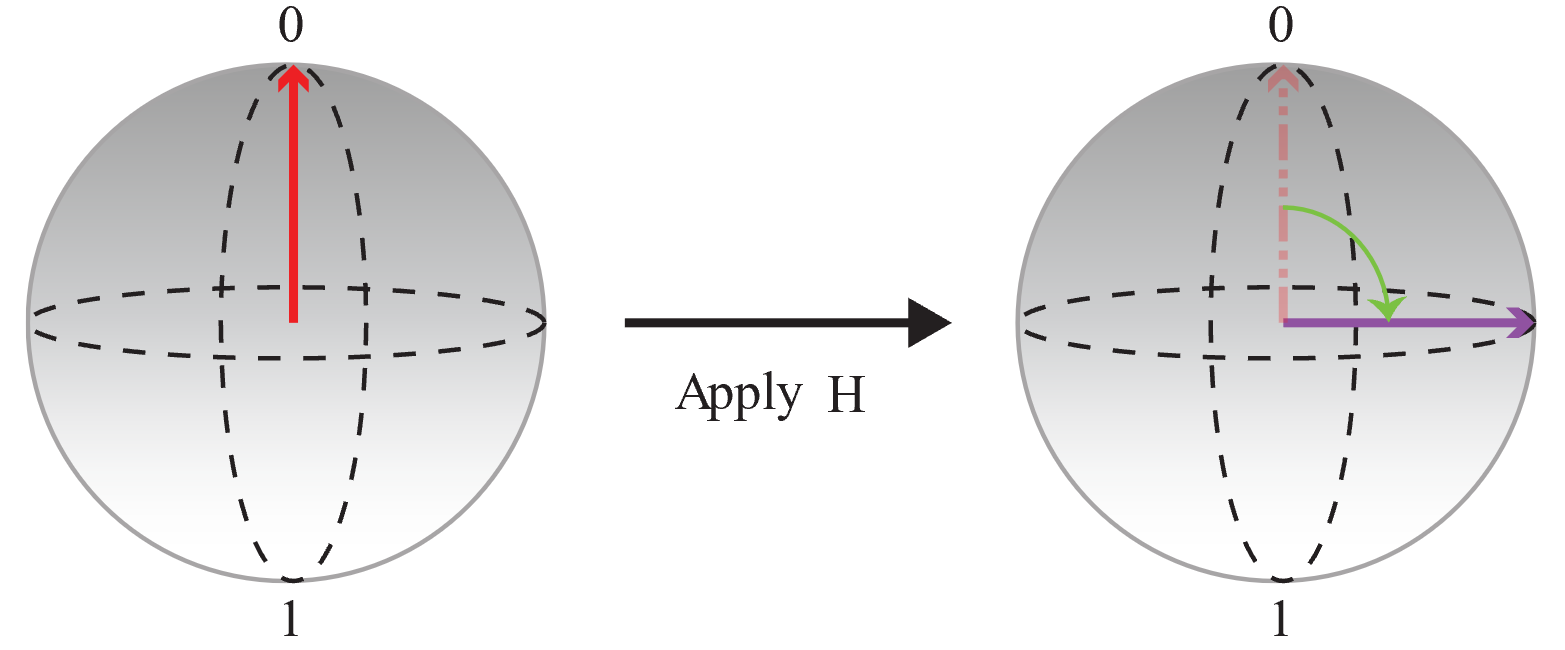

    Diagramma che mostra la preparazione di un qubit in sovrapposizione applicando il cancello hadamard.

  2. Quindi misurare il qubit e salvare l'output:

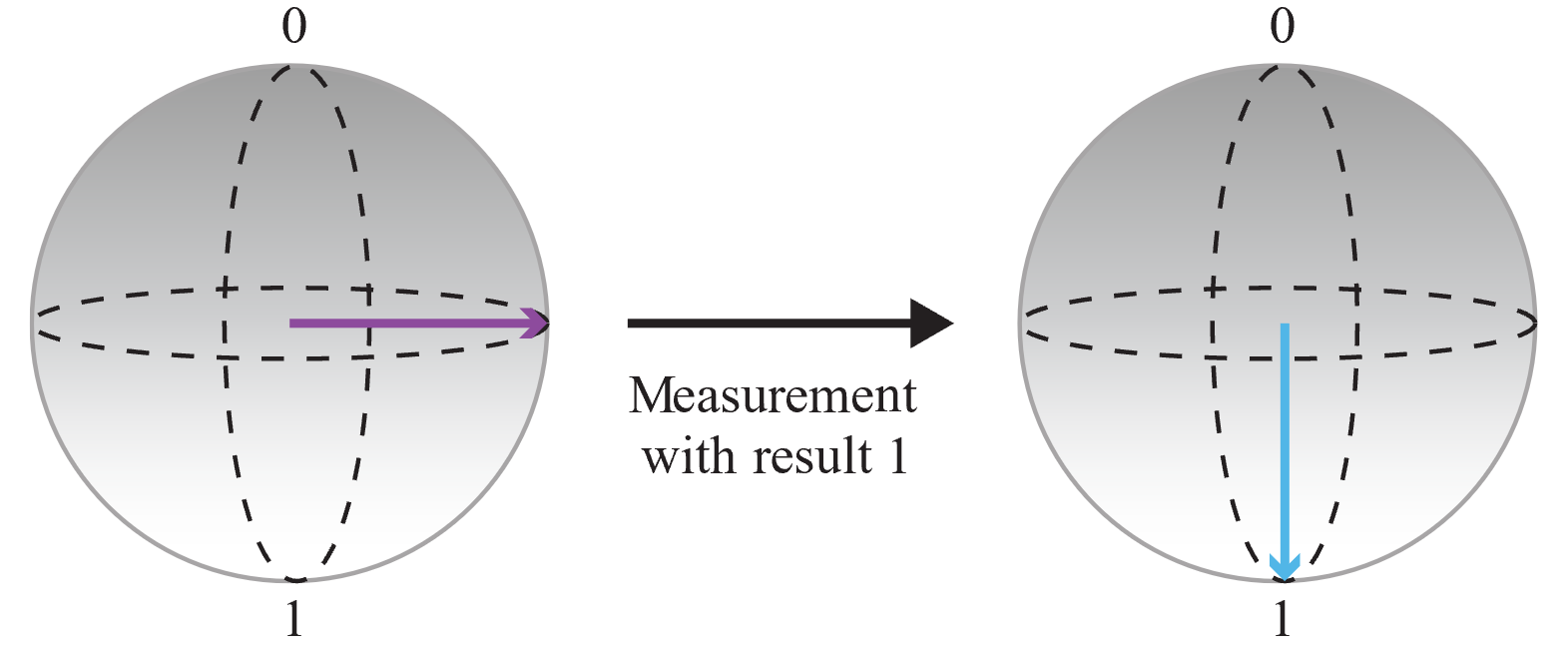
    Diagramma che mostra la misurazione di un qubit e il salvataggio dell'output.

Poiché il risultato della misurazione è casuale e le probabilità di misurare 0 e 1 sono identiche, si è ottenuto un bit completamente casuale. È possibile chiamare questa operazione più volte per creare numeri interi. Ad esempio, se si chiama l'operazione tre volte per ottenere tre bit casuali, è possibile creare numeri casuali a 3 bit, ovvero un numero casuale compreso tra 0 e 7.

Scrivere un generatore di numeri casuali completo

  1. Prima di tutto, è necessario aggiungere gli spazi dei nomi necessari Q# al programma. Per il generatore completo di numeri casuali, è necessario includere tre Q# spazi dei nomi: Microsoft.Quantum.Math, Microsoft.Quantum.Intrinsice Microsoft.Quantum.Convert.

    open Microsoft.Quantum.Convert;
open Microsoft.Quantum.Intrinsic;
open Microsoft.Quantum.Math;

  2. Definire quindi l'operazione GenerateRandomNumberInRange . Questa operazione chiama ripetutamente l'operazione GenerateRandomBit per creare una stringa di bit.

        /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }

    Esaminare per un attimo il nuovo codice.

    • È necessario calcolare il numero di bit necessari per esprimere numeri interi fino a max. La BitSizeI funzione dello Microsoft.Quantum.Math spazio dei nomi converte un numero intero nel numero di bit necessari per rappresentarlo.
    • L'operazione SampleRandomNumberInRange usa un ciclo for per generare numeri casuali fino a quando non viene generato un valore uguale o minore di max. Il for ciclo funziona esattamente come un for ciclo in altri linguaggi di programmazione.
    • La variabile è una variabile bits modificabile. Una variabile modificabile può cambiare durante il calcolo. Usare la direttiva set per cambiare il valore di una variabile modificabile.
    • La ResultArrayAsInt funzione proviene dallo spazio dei Microsoft.Quantum.Convert nomi . Questa funzione converte la stringa di bit in un numero intero positivo.

  3. Infine, si aggiunge un punto di ingresso. In questo esempio, l'operazione Main è il punto di ingresso del programma. Chiama l'operazione GenerateRandomNumberInRange per generare un numero casuale compreso tra 0 e 100.

        @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }

    La direttiva let dichiara variabili che non cambiano durante il calcolo. Qui definiamo il valore massimo come 100.

  4. Il codice completo per il generatore di numeri casuali è il seguente:

namespace QuantumRandomNumberGenerator {
    open Microsoft.Quantum.Convert;
    open Microsoft.Quantum.Intrinsic;
    open Microsoft.Quantum.Math;

    @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }

    /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }

    operation GenerateRandomBit() : Result {
        // Allocate a qubit.
        use q = Qubit();

        // Set the qubit into superposition of 0 and 1 using the Hadamard 
        H(q);

        // At this point the qubit `q` has 50% chance of being measured in the
        // |0〉 state and 50% chance of being measured in the |1〉 state.
        // Measure the qubit value using the `M` operation, and store the
        // measurement value in the `result` variable.
        let result = M(q);

        // Reset qubit to the |0〉 state.
        // Qubits must be in the |0〉 state by the time they are released.
        Reset(q);

        // Return the result of the measurement.
        return result;
    }
}

Eseguire il programma di generazione di numeri casuali

È possibile eseguire il programma in Copilot in Azure Quantum e in Visual Studio Code come applicazione autonoma Q# o usando un programma host Python.

È possibile testare il Q# codice con copilot in Azure Quantum gratuitamente. È sufficiente un account di posta elettronica Microsoft (MSA). Per altre informazioni sul Copilot in Azure Quantum, vedere Esplorare Azure Quantum.

  1. Aprire Copilot in Azure Quantum nel browser.

  2. Copiare e incollare il codice seguente nell'editor di codice.

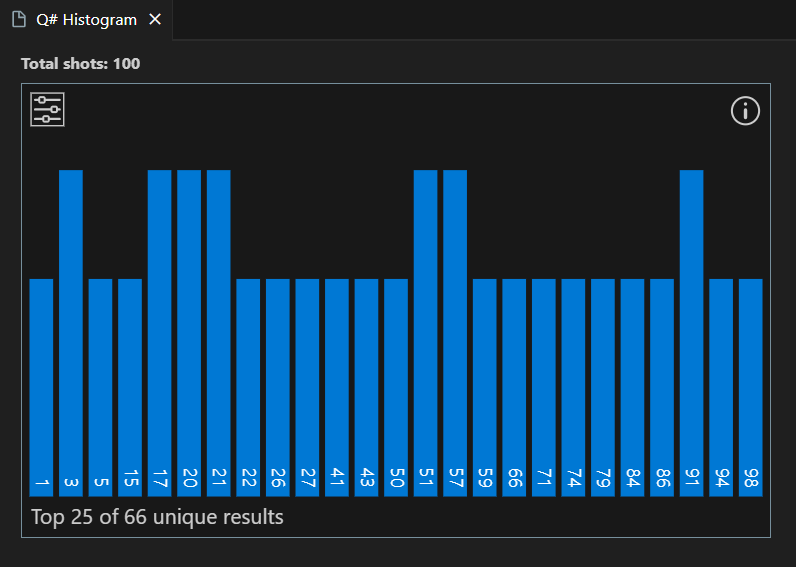
    namespace Tutorial {
    open Microsoft.Quantum.Convert;
    open Microsoft.Quantum.Intrinsic;
    open Microsoft.Quantum.Math;

    @EntryPoint()
    operation Main() : Int {
        let max = 100;
        Message($"Sampling a random number between 0 and {max}: ");

        // Generate random number in the 0..max range.
        return GenerateRandomNumberInRange(max);
    }

    /// # Summary
    /// Generates a random number between 0 and `max`.
    operation GenerateRandomNumberInRange(max : Int) : Int {
        // Determine the number of bits needed to represent `max` and store it
        // in the `nBits` variable. Then generate `nBits` random bits which will
        // represent the generated random number.
        mutable bits = [];
        let nBits = BitSizeI(max);
        for idxBit in 1..nBits {
            set bits += [GenerateRandomBit()];
        }
        let sample = ResultArrayAsInt(bits);

        // Return random number if it is within the requested range.
        // Generate it again if it is outside the range.
        return sample > max ? GenerateRandomNumberInRange(max) | sample;
    }

    /// # Summary
    /// Generates a random bit.
    operation GenerateRandomBit() : Result {
        // Allocate a qubit.
        use q = Qubit();

        // Set the qubit into superposition of 0 and 1 using the Hadamard 
        // operation `H`.
        H(q);

        // At this point the qubit `q` has 50% chance of being measured in the
        // |0〉 state and 50% chance of being measured in the |1〉 state.
        // Measure the qubit value using the `M` operation, and store the
        // measurement value in the `result` variable.
        let result = M(q);

        // Reset qubit to the |0〉 state.
        // Qubits must be in the |0〉 state by the time they are released.
        Reset(q);

        // Return the result of the measurement.
        return result;

        // Note that Qubit `q` is automatically released at the end of the block.
    }
}

  3. Selezionare il numero di scatti da eseguire e fare clic su Esegui.

  4. I risultati vengono visualizzati nell'istogramma e nei campi Risultati .

  5. Fare clic su Spiega codice per richiedere a Copilot di spiegare il codice.

Suggerimento

Da Copilot in Azure Quantum è possibile aprire il programma in VS Code per il Web facendo clic sul pulsante logo di VS Code nell'angolo destro dell'editor di codice.

Nota

Questo frammento di codice non viene attualmente eseguito in alcun hardware targetsAzure Quantum disponibile, perché il chiamabile ResultArrayAsInt richiede una QPU con profilo di calcolo completo.

Passaggi successivi

Esplorare altre esercitazioni su Q#: