Уравнения PRT (Direct3D 9)
Чтобы полностью понять шейдер, реализующий PRT, полезно получить формулу, которую шейдер использует для вычисления сияния выхода.
Для начала следующее уравнение является общим уравнением для вычисления выходного сияния в результате прямого освещения на диффузном объекте с произвольным удаленным освещением.

где:
| Параметр | Описание |
|---|---|
| Rp | Выходная сияние в вершине p. Вычисляется на каждой вершине сетки. |
| pd | Альбедо поверхности. |
| pi | Константа, используемая в качестве фактора нормализации энергопотребления. |
| L(s) | Среда освещения (источник сияния). |
| Vp₍s₎ | Двоичная функция видимости для точки p. Это 1, если точка может видеть свет, 0, если нет. |
| Hnp₍s₎ | Косинус из закона Ламберта. Равно max((Np· s), 0), где Np — норма поверхности в точке p. |
| s | Переменная, которая интегрируется над сферой. |
С помощью сферических базовых функций, таких как сферические гармоники, следующее уравнение приблизит среду освещения.
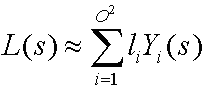
где:
| Параметр | Описание |
|---|---|
| L(s) | Среда освещения (источник сияния). |
| i | Целое число, которое суммирует по количеству базовых функций. |
| O | Порядок сферических гармоник. |
| li | Коэффициент. |
| Yi(s) | Некоторые базовые функции над сферой. |
Коллекция этих коэффициентов L', обеспечивает оптимальное приближение для функции L(s) с базовыми функциями Y. Подстановка и распределение дает следующее уравнение.
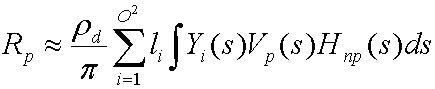
Интеграл Yi(s)Vp₍s₎Hnp₍s₎ — это коэффициент передачи tpi , который симулятор предварительно вычисляет для каждой вершины в сетке. Подстановка этого приводит к следующему уравнению.
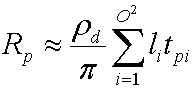
При изменении этого параметра на векторную нотацию для каждого канала будет вычислено следующее несжатые уравнения.
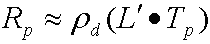
где:
| Параметр | Описание |
|---|---|
| Rp | Выходная сияние в вершине p. |
| pd | Альбедо поверхности. |
| L' | Вектор li, и — проекция исходного сияния в сферические гармонические базовые функции. Это вектор order² сферических гармонических коэффициентов. |
| Tp | Вектор передачи order² для вершины p. Симулятор делит коэффициенты передачи на p. |
Оба этих вектора являются вектором order² сферических гармонических коэффициентов, поэтому обратите внимание, что это просто точечное произведение. В зависимости от порядка точка может быть дорогостоящей, поэтому можно использовать сжатие. Алгоритм с именем Анализ кластеризованных основных компонентов (CPCA) эффективно сжимает данные. Это позволяет использовать сферическую гармонию более высокого порядка, которая приводит к более резким теням.
CPCA предоставляет следующее уравнение для приближения вектора передачи.
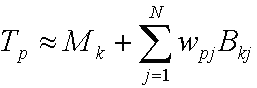
где:
| Параметр | Описание |
|---|---|
| Tp | Вектор передачи для вершины p. |
| Mk | Среднее значение для кластера k. |
| j | Целое число, которое суммирует по количеству векторов PCA. |
| N | Число векторов PCA. |
| wpj | Jth PCA вес для точки p. |
| Bkj | Базовый вектор Jth PCA для кластера k. |
Кластер — это просто некоторое количество вершин, использующих один и тот же средний вектор. Ниже описано, как получить среднее значение кластера, весовые коэффициенты PCA, базовые векторы PCA и идентификаторы кластера для вершин.
Замена этих двух уравнений приводит к следующим результату:
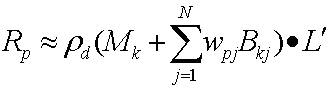
Затем распределение точечного продукта дает следующее уравнение.
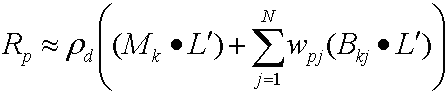
Потому что оба (Mk· L') и (Bkj· L') являются константой для каждой вершины. Выборка вычисляет эти значения с помощью ЦП и передает их в виде констант в вершинный шейдер; Поскольку wpj меняется для каждой вершины, образец сохраняет эти данные для каждой вершины в буфере вершин.
Связанные темы
Обратная связь
Ожидается в ближайшее время: в течение 2024 года мы постепенно откажемся от GitHub Issues как механизма обратной связи для контента и заменим его новой системой обратной связи. Дополнительные сведения см. в разделе https://aka.ms/ContentUserFeedback.
Отправить и просмотреть отзыв по