نتائج نماذج التعلم الآلي

تناقش هذم المقالة مقاييس الالتباس ومشكلات التصنيف والدقة في نماذج التعلم الآلي (ML). والغرض هو تعزيز فهمك للدقة في نتائج توقع التعلم الآلي. يتضمن الجمهور المستهدف المهندسين والمحللين والمديرين الذي يرغبون في إنشاء المعرفة والمهارات الخاصة بهم في علم البيانات.

مقياس الالتباس

بعد التدرب على مشكلة التعلم الآلي المراقب على مجموعة من البيانات التاريخية، فإنه يتم اختبارها باستخدام البيانات المقتطعة من عملية التدريب. وبهذه الطريقة، يمكنك مقارنة التوقعات من النموذج المدرب بالقيم الفعلية. يوفر مقياس الالتباس وسيلة لتقييم مدى نجاح مشكلة التصنيف والمكان الذي يمثل فيه الأخطاء (أي، حيث يتم "الخلط").

على سبيل المثال، الهدف الخاص بك هو التنبؤ سواء كان الحيوان الأليف كلب أو قطة، استنادًا إلى بعض السمات الفعلية والسلوكية. إذا كان لديك مجموعة بيانات اختبار تحتوي على 30 كلبًا و20 قطة، فقد يكون مقياس الالتباس مشابهًا للرسم التوضيحي التالي.

تمثل الأرقام الموجودة في الخلايا الخضراء التوقعات الصحيحة. كما ترى، توقع النموذج نسبة مئوية أعلى من عدد القطط الفعلي بشكل صحيح. تكون الدقة الإجمالية للنموذج سهلة الحساب. في هذه الحالة، 42 ÷ 50 أو 0.84.

مصنفات متعددة الفئات في مقياس الالتباس

يتم التركيز على معظم المناقشات حول مقياس الالتباس على مصنفات ثنائية، كما في المثال السابق. هذه حالة خاصة، حيث يمكن اعتبار المقاييس الأخرى مثل الحساسية والاستدعاء.

بعد ذلك، سنقوم بمراعاة مشكلة التصنيف لسيناريو مالي يحتوي على ثلاث حالات. ويقوم النموذج بتوقع ما إذا كان سيتم دفع فاتورة العميل في الوقت المحدد أم متأخرة أم متأخرة جدًا. على سبيل المثال، من أصل 100 فاتورة اختبار، فإنه يتم دفع 50 في الوقت المحدد، ويتم دفع 35 متأخرة، ويتم دفع 15 فاتورة متأخرة جدًا. في هذه الحالة، قد ينتج نموذج مقياس التباس يشبه الرسم التوضيحي التالي.

]

يوفر مقياس الالتباس مزيد من المعلومات بشكل ملحوظ أكثر من قياس دقه بسيط. ومع ذلك، فإنه لا يزال من السهل فهمه نسبيًا. يخبرك مقياس الالتباس ما إذا كان لديك مجموعة بيانات متوازنة حيث يكون لفئات المخرجات عمليات جرد مشابهة. بالنسبة للسيناريو متعدد الفئات، فإنه يخبرك عن مدى التنبؤ الذي قد يكون عليه عندما تكون فئات المخرجات ترتيبية، كما في المثال السابق حول مدفوعات العميل.

دقة النموذج

وتتميز مقاييس الدقة المختلفة لتحديد جودة النموذج.

نظرًا لأن الدقة هي أداة قياسية لفهمها، فإنها تعد نقطة بداية جيدة لشرح نموذج إلى أشخاص آخرين، خاصة لمستخدمي النموذج الذي هم لا يكونوا علماء البيانات. لا توجد أي فهم للإحصائيات المطلوبة لفهم الدقة الخاصة بالنموذج. عند توفر مقياس الالتباس، فإنه يوفر مزيدًا من نتيجة التحليلات في أداء النموذج.

ومع ذلك، بالنسبة لفهم أكثر شمولاً، فإنه يجب ملاحظة العديد من التحديات المرتبطة بالدقة. تعتمد فائدة القياس على سياق المشكلة. السؤال الذي غالبًا ما يبرز بالنسبة لأداء النموذج هو، "ما مدى كفاءة النموذج؟" ومع ذلك، فإن إجابة هذا السؤال ليست بالضرورة مباشرة. خذ بعين الاعتبار مقياس الالتباس التالي (نموذج 2).

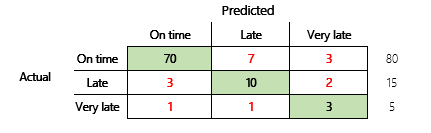
تُظهر العمليات الحسابية السريعة أن دقه هذا النموذج هي (70 + 10 + 3) ÷ 100 أو 0.83. على السطح، تبدو هذه النتيجة أفضل من نتيجة لنموذج متعدد الفئات السابق (نموذج 1)، والذي له دقة 0.73. ولكنه هل هو أفضل؟

لبدء التعامل مع هذا السؤال، فكر بدقة لتخمين naïve. بالنسبة لمشكلة التصنيف، سيعمل التنبؤ البسيط دائمًا على التنبؤ بالفئة الأكثر شيوعًا. النسبة للنموذج 1، سيكون هذا التخمين "في الوقت المحدد" وسينتج عنه دقه 0.50. سيكون التخمين بالنسبة للنموذج 2 "في الوقت المحدد" أيضًا وسينتج عنه دقه 0.80. ونظرًا لأن النموذج 1 يحسن تخمين naïve في التخمين بمقدار 0.73 – 0.50 = 0.23، بينما يحسن النموذج 2 تخمين naïve بمقدار 0.83-0.80 = 0.03، فإن النموذج 1 يُعد نموذجًا أفضل، حتى ولو كانت دقته أقل. ويكشف الحساب أن التقييم الفعال لجودة النموذج يتطلب سياقًا أكبر من قيمة الدقة.

هناك جانب آخر جدير بالملاحظة. خذ بعين الاعتبار سيناريو حيث يُستخدم الاختبار الطبي للكشف عن المرض في المريض. وتُعد هذه المشكلة مشكلة في التصنيف الثنائي حيث تشير النتيجة الموجبة إلى أن المريض يعاني من المرض. في هذا السيناريو، يجب عليك التفكير في تأثير الأخطاء التالية:

• نتائج إيجابية خاطئة، حيث يشير الاختبار إلى أن المريضة تعاني من المرض، ولكن المريض لا يعاني منه حقًا.
• نتائج سلبية خاطئة، حيث يشير الاختبار إلى أن المريضة لا تعاني من المرض، ولكن المريض يعاني منه حقًا.

من الواضح، كلا نوعي الخطأ غير مرغوب فيهما، ولكن ما الأمر الأسوأ؟ مرة أخرى، الأمر على حسب. في حالة وجود مرض مهدد للحياة يتطلب معالجة سريعة، يكون لتقليل السلبيات الخاطئة (التي نأمل أن تتبعها اختبارات إضافية) الأولوية. في المواقف الأخرى، الأقل أهمية، فقد يقوم منشئو النماذج بتقليل الإيجابيات الخاطئة بدلاً من ذلك. وبأي معدل، فإن الخاتمة المعقولة هي أنه يمكن تحديد جودة النموذج بفاعلية، ويجب أن يكون لديك مزيد من المعلومات أكثر من المعلومات التي يوفرها مقياس الدقة.

التوصيات

تعد الدقة أداة هامة للتواصل مع خبراء المجال الذين هم ليسوا على دراية بالإحصائيات. ومع ذلك، لجعل المعلومات مفيدة، فمن الضروري توفير سياق إضافي مع قيمة الدقة.

بالنسبة لسيناريو توقع الدفع، يمكنك تعيين هدف لنموذج التعلم الآلي الذي يتضمن عواملاً في سلوكيات دفع مختلفة. الهدف هو أن النموذج يجب أن يتحسن على تخمين naïve عن طريق تقليل عدد الإجابات غير الصحيحة بنسبه 50 بالمئة على الأقل. وبمعني آخر، فإنك تحتاج إلى دقة هدف تقوم بتقسيم المختلف بين دقة تخمين naïve ونسبة 100 بالمائة.

يلخص الجدول التالي هذه القاعدة لمقاييس الالتباس في هذه المقالة.

النموذج	تخمين Naïve	الهدف	دقة النموذج	هل يتحقق الهدف؟
نموذج 1	0.50	0.75	0.73	تقريبًا. يتحسن هذا النموذج بشكل ملحوظ عند التخمين.
نموذج 2	0.80	0.90	0.83	الرقم التحسين مطلوب.

دقة التصنيف F1

يُعد الاعتبار الأخير في هذه المقالة مقياسًا أكثر تقدمًا لأداء التعلم الآلي للتصنيف بدقة F1.

وقبل أن يتم تحديد الدقة F1، فإنه يجب تقديم قياسين إضافيين: الدقة والاستدعاء. تشير الدقة إلى عدد العدد الإجمالي من التوقعات التي يتم تحديدها كأرقام موجبة معينة بشكل صحيح. يعرف هذا القياس أيضًا بقيمة تنبؤية موجبة. يعد الاستدعاء هو العدد الإجمالي للحالات الإيجابية الفعلية التي تم توقعها بشكل صحيح. ويعرف هذا القياس أيضًا باسم الحساسية.

في مقياس الالتباس في الرسم التوضيحي السابق، يتم حساب هذه المقاييس بالطريقة التالية:

• الدقة = إيجابي صحيح ÷ (إيجابي صحيح + إيجابي خاطئ)
• الاستدعاء = الإيجابي الصحيح ÷ (الإيجابي الصحيح + السلبي الخاطئ)

ويدمج المقياس F1 بين الدقة والاستدعاء. تكون النتيجة هي الوسط التوافقي للقيمتين. ويتم حسابهما بالطريقة التالية:

• F1 = 2 × (الدقة × الاستدعاء) ÷ (الدقة + الاستدعاء)

هيا نلقي نظرة على أحد الأمثلة الملموسة. سابقًا في هذه المقالة ، كان هناك مثال على النموذج الذي توقع ما إذا كان الحيوان عبارة عن كلب أو قطة. يتم تكرار الرسم التوضيحي هنا.

وإليك النتائج في حالة استخدام "كلب" كإجابة إيجابية.

• الدقة = 24 ÷ (24 + 2) = 0.9231
• استدعاء = 24 ÷ (24 + 6) = 0.8
• F1 = 2 × (0.9231 × 0.8) ÷ (0.9231 + 0.8) = 0.8572

كما ترى ، تكون القيمة F1 بين قيم الدقة والاستدعاء.

وعلى الرغم من أن دقة F1 ليست سهلة الفهم، فإنها تضيف فارق بسيط إلى رقم الدقة الأساسي. كما يمكن أن تساعد في مجموعات بيانات غير متوازنة، كما ستُظهر المناقشة التالية.

يقارن قسم دقة النموذج الخاص بهذا الموضوع بين مقياسي الالتباس التاليين. وعلى الرغم من أن النموذج الأول به دقة منخفضة، فقد يبدو نموذجًا أكثر إفادة لأنه يعرض تحسينًا أكبر من التخمين الافتراضي للدفع في الوقت المحدد.

هيا نقوم بالاطلاع على كيفية مقارنة هذين النموذجين عند استخدام النتيجة F1. وعوامل التسجيل F1 بالدقة والاستدعاء لكل حالة، ويقوم حساب الماكرو F1 بعد ذلك بحساب متوسط النتيجة F1 عبر الحالات لتحديد النتيجة الإجمالية F1. هناك متغيرات أخرى لـ F1، ولكن من الأفضل أن تراعي إصدار الماكرو، بما في ذلك الاعتبارات المتساوية التي تُعطى لكافة الحالات الثلاثة.

لتبسيط عمليات الحساب، تم إنشاء عينة من الصفائف لتطابق القيم الفعلية والمتوقعة. تستخدم هذه الصفائف مكتبة مقاييس سكليرن في بيثون لحساب القيم. فيما يلي النتيجة.

النموذج	تخمين Naïve	الدقة	ماكرو F1
نموذج 1	0.5	0.73	0.67
نموذج 2	0.80	0.83	0.66

لمزيد من التفاصيل حول كيفية عمل هذه العملية الحسابية، فيما يلي تقرير تصنيف sklearn.metrics للنموذج 1. يتم تمثيل الثلاث حالات "في الوقت المحدد" و "متأخرة" و "متأخرة جدًا" بالصفوف التي تسمي 1 و 2 و 3 على التوالي. يمثل "معدل الماكرو" متوسط عمود "النتيجة f1" فقط.

	الدقة	استدعاء	نقطة f1
1	0.83	0.80	0.82
2	0.68	0.71	0.69
3	0.50	0.50	0.50

ونظرًا لأن هذه النتائج يتم عرضها، فإن النموذجين يحتويان على معدلات دقة ماكرو F1 متطابقة تقريبًا. في هذه الحالات والعديد من الحالات الأخرى، توفر دقة F1 مؤشرًا أفضل لقدرة الطراز. وكما هو الحال بالنسبة للدقة، يتطلب تفسير النتائج فهم الغرض الأكثر أهمية في النموذج.