تقييم أنواع مختلفة من التجميع
تدريب نموذج تكوين أنظمة المجموعات
هناك العديد من الخوارزميات التي يمكنك استخدامها لتكوين أنظمة المجموعات. إحدى أكثر الخوارزميات استخداماً هي مجموعة K-Means والتي تتكون في أبسط أشكالها من الخطوات التالية:
- يتم تحويل قيم الميزة لتعريف إحداثيات n الأبعاد (حيث n هو عدد الميزات). في مثال الزهرة، لدينا ميزتان: عدد البتلات وعدد الأوراق. لذلك، يحتوي متجه الميزة على إحداثيتين يمكننا استخدامهما لرسم نقاط البيانات في مساحة ثنائية الأبعاد من الناحية المفاهيمية.
- يمكنك تحديد عدد المجموعات التي تريد استخدامها لتجميع الزهور - قم باستدعاء هذه القيمة k. على سبيل المثال، لإنشاء ثلاث مجموعات، يمكنك استخدام قيمة k وهي 3. ثم يتم رسم نقاط k في إحداثيات عشوائية. تصبح هذه النقاط هي النقاط المركزية لكل مجموعة، لذلك تسمى النقاط المركزية.
- يتم تعيين كل نقطة بيانات (في هذه الحالة زهرة) إلى أقرب نقطة مركزية لها.
- يتم نقل كل نقطة مركزية إلى مركز نقاط البيانات المعينة لها استنادًا إلى متوسط المسافة بين النقاط.
- بعد نقل النقطة المركزية، قد تكون نقاط البيانات الآن أقرب إلى نقطة مركزية مختلفة، لذلك يتم إعادة تعيين نقاط البيانات إلى المجموعات استنادا إلى أقرب نقطة مركزية جديدة.
- تتكرر خطوات حركة النقاط المركزية وإعادة تخصيص نظام المجموعة حتى تصبح المجموعات مستقرة أو يتم الوصول إلى الحد الأقصى المحدد مسبقا من التكرارات.
يظهر الرسم المتحرك التالي هذه العملية:

التجميع الهرمي
التجميع الهرمي هو نوع آخر من خوارزمية التجميع التي تنتمي فيها المجموعات نفسها إلى مجموعات أكبر، والتي تنتمي إلى مجموعات أكبر، وما إلى ذلك. وتتمثل النتيجة في أن نقاط البيانات يمكن أن تكون مجموعات بدرجات متفاوتة من الدقة: نتيجة بعدد كبير من المجموعات الصغيرة جداً والدقيقة، أو نتيجة بعدد صغير من المجموعات الأكبر.
على سبيل المثال، إذا طبقنا التجميع على معاني الكلمات، فقد نحصل على مجموعة تحتوي على صفات خاصة بالعواطف ('غاضب'، 'سعيد'، وهكذا). تنتمي هذه المجموعة إلى مجموعة تحتوي على جميع الصفات ذات الصلة بالإنسان ('سعيد'، 'وسيم'، 'شاب')، والتي تنتمي إلى مجموعة أعلى تحتوي على جميع الصفات ('سعيد'، 'أخضر'، 'وسيم'، 'صعب'، وهكذا).
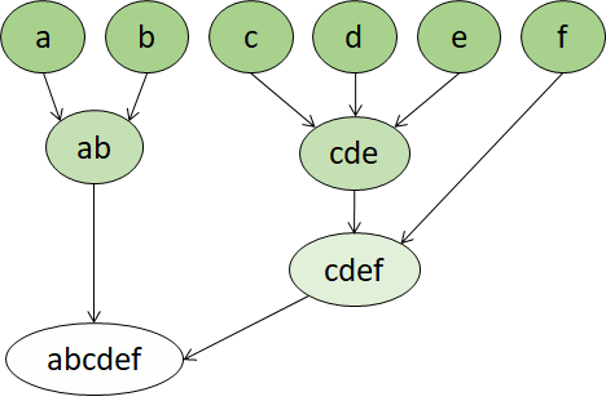
يعد التجميع الهرمي مفيداً ليس فقط لتقسيم البيانات إلى مجموعات، ولكن أيضاً لفهم العلاقات بين هذه المجموعات. تتمثل الميزة الرئيسية للمجموعات الهرمية في أنها لا تتطلب تحديد عدد المجموعات مسبقا. ويمكن أن توفر في بعض الأحيان نتائج أكثر قابلية للتفسير من الأساليب غير الهرمية. العيوب الرئيسية هي أن هذه الأساليب يمكن أن تستغرق وقتا أطول للحساب من الأساليب الأبسط، وأحيانا لا تكون مناسبة لمجموعات البيانات الكبيرة.