Hinweis
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, sich anzumelden oder das Verzeichnis zu wechseln.
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, das Verzeichnis zu wechseln.
Erfahren Sie, wie Sie Mithilfe von SkiaSharp Bögen auf drei verschiedene Arten definieren.
Ein Bogen ist eine Kurve auf dem Umfang einer Ellipse, z. B. die abgerundeten Teile dieses Unendlichkeitszeichens:

Trotz der Einfachheit dieser Definition gibt es keine Möglichkeit, eine Bogenzeichnungsfunktion zu definieren, die jedem Bedarf entspricht, und daher kein Konsens zwischen Grafiksystemen der besten Methode zum Zeichnen eines Bogens. Aus diesem Grund beschränkt sich die SKPath Klasse nicht auf nur einen Ansatz.
SKPath definiert eine AddArc Methode, fünf verschiedene ArcTo Methoden und zwei relative RArcTo Methoden. Diese Methoden sind in drei Kategorien unterteilt, die drei sehr unterschiedliche Ansätze zum Angeben eines Bogens darstellen. Welche Sie verwenden, hängt von den verfügbaren Informationen ab, um den Bogen zu definieren, und wie dieser Bogen mit den anderen Grafiken passt, die Sie zeichnen.
Der Winkelbogen
Der Winkelbogenansatz zum Zeichnen von Bögen erfordert, dass Sie ein Rechteck angeben, das eine Ellipse begrenzt. Der Bogen auf dem Umfang dieser Ellipse wird durch Winkel vom Mittelpunkt der Ellipse angegeben, die den Anfang des Bogens und seine Länge angeben. Zwei verschiedene Methoden zeichnen Winkelbögen. Dies sind die AddArc Methode und die ArcTo Methode:
public void AddArc (SKRect oval, Single startAngle, Single sweepAngle)
public void ArcTo (SKRect oval, Single startAngle, Single sweepAngle, Boolean forceMoveTo)
Diese Methoden sind identisch mit den Methoden Android AddArc und [ArcTo]xref:Android.Graphics.Path.ArcTo*). Die iOS-Methode AddArc ist ähnlich, ist aber auf Bogen auf den Umfang eines Kreises beschränkt, anstatt auf eine Ellipse generalisiert.
Beide Methoden beginnen mit einem SKRect Wert, der sowohl den Standort als auch die Größe einer Ellipse definiert:

Der Bogen ist Teil des Umfangs dieser Ellipse.
Das startAngle Argument ist ein Winkel im Uhrzeigersinn in Grad relativ zu einer horizontalen Linie, die von der Mitte der Auslassungspunkte nach rechts gezeichnet wird. Das sweepAngle Argument ist relativ zum startAngle. Hier sind startAngle und sweepAngle werte von 60 Grad bzw. 100 Grad:

Der Bogen beginnt am Anfangswinkel. Die Länge wird durch den Aufräumwinkel gesteuert. Der Bogen ist hier rot dargestellt:
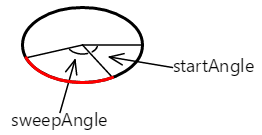
Die Kurve, die dem Pfad mit der AddArc Methode ArcTo hinzugefügt wurde, ist einfach der Teil des Umfangs der Ellipse:

sweepAngle Die startAngle Argumente können negativ sein: Der Bogen ist im Uhrzeigersinn für positive Werte von sweepAngle und gegen den Uhrzeigersinn für negative Werte.
AddArc Definiert jedoch keine geschlossene Kontur. Wenn Sie danach aufrufenLineTo, wird eine Linie vom Ende des Bogens bis zum Punkt in der LineTo Methode gezeichnet, und dasselbe gilt für ArcTo.AddArc
AddArc startet automatisch eine neue Kontur und entspricht funktionell einem Aufruf ArcTo mit einem endgültigen Argument von true:
path.ArcTo (oval, startAngle, sweepAngle, true);
Dieses letzte Argument wird aufgerufen forceMoveTo, und es verursacht effektiv einen MoveTo Aufruf am Anfang des Bogens. Das beginnt eine neue Kontur. Dies ist nicht der Fall mit einem letzten Argument von false:
path.ArcTo (oval, startAngle, sweepAngle, false);
Diese Version von ArcTo zeichnet eine Linie von der aktuellen Position bis zum Anfang des Bogens. Dies bedeutet, dass der Bogen irgendwo in der Mitte einer größeren Kontur sein kann.
Auf der Seite "Winkelbogen " können Sie zwei Schieberegler verwenden, um die Anfangs- und Aufräumwinkel anzugeben. Die XAML-Datei instanziiert zwei Slider Elemente und ein SKCanvasView. Der PaintCanvas Handler in der datei AngleArcPage.xaml.cs zeichnet sowohl das Oval als auch den Bogen mit zwei SKPaint Objekten, die als Felder definiert sind:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKRect rect = new SKRect(100, 100, info.Width - 100, info.Height - 100);
float startAngle = (float)startAngleSlider.Value;
float sweepAngle = (float)sweepAngleSlider.Value;
canvas.DrawOval(rect, outlinePaint);
using (SKPath path = new SKPath())
{
path.AddArc(rect, startAngle, sweepAngle);
canvas.DrawPath(path, arcPaint);
}
}
Wie Sie sehen können, können sowohl der Anfangswinkel als auch der Aufräumwinkel negative Werte annehmen:
Dieser Ansatz zum Generieren eines Bogens ist algorithmisch am einfachsten, und es ist einfach, die parametrischen Gleichungen abzuleiten, die den Bogen beschreiben. Wenn Sie die Größe und Position der Ellipse kennen und die Anfangs- und Aufräumwinkel kennen, können die Anfangs- und Endpunkte des Bogens mit einfacher Trigonometrie berechnet werden:
x = oval.MidX + (oval.Width / 2) * cos(angle)
y = oval.MidY + (oval.Height / 2) * sin(angle)
Der angle Wert ist entweder startAngle oder startAngle + sweepAngle.
Die Verwendung von zwei Winkeln zum Definieren eines Bogens eignet sich am besten für Fälle, in denen Sie die Winkellänge des Bogens kennen, den Sie zeichnen möchten, z. B. um ein Kreisdiagramm zu erstellen. Auf der Seite "Explodiertes Kreisdiagramm" wird dies veranschaulicht. Die ExplodedPieChartPage Klasse verwendet eine interne Klasse, um einige fabricierte Daten und Farben zu definieren:
class ChartData
{
public ChartData(int value, SKColor color)
{
Value = value;
Color = color;
}
public int Value { private set; get; }
public SKColor Color { private set; get; }
}
ChartData[] chartData =
{
new ChartData(45, SKColors.Red),
new ChartData(13, SKColors.Green),
new ChartData(27, SKColors.Blue),
new ChartData(19, SKColors.Magenta),
new ChartData(40, SKColors.Cyan),
new ChartData(22, SKColors.Brown),
new ChartData(29, SKColors.Gray)
};
Der PaintSurface Handler durchläuft zunächst die Elemente, um eine totalValues Zahl zu berechnen. Daraus kann die Größe jedes Elements als Bruchteil der Summe bestimmt und in einen Winkel konvertiert werden:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
int totalValues = 0;
foreach (ChartData item in chartData)
{
totalValues += item.Value;
}
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float explodeOffset = 50;
float radius = Math.Min(info.Width / 2, info.Height / 2) - 2 * explodeOffset;
SKRect rect = new SKRect(center.X - radius, center.Y - radius,
center.X + radius, center.Y + radius);
float startAngle = 0;
foreach (ChartData item in chartData)
{
float sweepAngle = 360f * item.Value / totalValues;
using (SKPath path = new SKPath())
using (SKPaint fillPaint = new SKPaint())
using (SKPaint outlinePaint = new SKPaint())
{
path.MoveTo(center);
path.ArcTo(rect, startAngle, sweepAngle, false);
path.Close();
fillPaint.Style = SKPaintStyle.Fill;
fillPaint.Color = item.Color;
outlinePaint.Style = SKPaintStyle.Stroke;
outlinePaint.StrokeWidth = 5;
outlinePaint.Color = SKColors.Black;
// Calculate "explode" transform
float angle = startAngle + 0.5f * sweepAngle;
float x = explodeOffset * (float)Math.Cos(Math.PI * angle / 180);
float y = explodeOffset * (float)Math.Sin(Math.PI * angle / 180);
canvas.Save();
canvas.Translate(x, y);
// Fill and stroke the path
canvas.DrawPath(path, fillPaint);
canvas.DrawPath(path, outlinePaint);
canvas.Restore();
}
startAngle += sweepAngle;
}
}
Für jedes Kreissegment wird ein neues SKPath Objekt erstellt. Der Pfad besteht aus einer Linie aus der Mitte, dann einer ArcTo , um den Bogen zu zeichnen, und eine weitere Linie zurück zur Mitte ergebnisse des Close Anrufs. Dieses Programm zeigt "explodierte" Kreissegmente an, indem sie alle von der Mitte um 50 Pixel aus der Mitte bewegen. Für diesen Vorgang ist ein Vektor in Richtung des Mittelpunkts des Aufräumwinkels für jedes Segment erforderlich:
Um zu sehen, wie es ohne die "Explosion" aussieht, kommentieren Sie einfach den Translate Anruf:
Der Tangensbogen
Der zweite Von diesem Bogen unterstützte SKPath Bogentyp ist der Tangensbogen, der so genannt wird, weil der Bogen der Umfang eines Kreises ist, der zu zwei verbundenen Linien tangensiert ist.
Ein Tangensbogen wird einem Pfad mit einem Aufruf der ArcTo Methode mit zwei SKPoint Parametern oder der ArcTo Überladung mit separaten Single Parametern für die Punkte hinzugefügt:
public void ArcTo (SKPoint point1, SKPoint point2, Single radius)
public void ArcTo (Single x1, Single y1, Single x2, Single y2, Single radius)
Diese ArcTo Methode ähnelt der PostScript-Funktion arct (Seite 532) und der iOS-Methode AddArcToPoint .
Die ArcTo Methode umfasst drei Punkte:
- Der aktuelle Punkt der Kontur oder der Punkt (0, 0) wenn
MoveTonicht aufgerufen wurde - Das erste Punktargument auf die
ArcToMethode, der als Eckpunkt bezeichnet wird - Das zweite Punktargument, das
ArcToals Zielpunkt bezeichnet wird:

Diese drei Punkte definieren zwei verbundene Linien:

Wenn die drei Punkte kolinear sind , d. h. wenn sie auf derselben geraden Linie liegen , wird kein Bogen gezeichnet.
Die ArcTo Methode enthält auch einen radius Parameter. Dadurch wird der Radius eines Kreises definiert:

Der Tangensbogen wird für eine Ellipse nicht generalisiert.
Wenn sich die beiden Linien in einem beliebigen Winkel treffen, kann dieser Kreis zwischen diesen Linien eingefügt werden, sodass er für beide Linien tangens ist:

Die Kurve, die der Kontur hinzugefügt wird, berührt keine der in der ArcTo Methode angegebenen Punkte. Sie besteht aus einer geraden Linie vom aktuellen Punkt zum ersten Tangentenpunkt und einem Bogen, der am zweiten Tangentenpunkt endet, der hier in Rot dargestellt wird:

Hier ist die letzte gerade Linie und der Bogen, die der Kontur hinzugefügt wird:

Die Kontur kann vom zweiten Tangenspunkt fortgesetzt werden.
Mit der Tangensbogenseite können Sie mit dem Tangentenbogen experimentieren. Dies ist die erste von mehreren Seiten, die von InteractivePageabgeleitet werden, die einige praktische SKPaint Objekte definiert und die Verarbeitung durchführt TouchPoint :
public class InteractivePage : ContentPage
{
protected SKCanvasView baseCanvasView;
protected TouchPoint[] touchPoints;
protected SKPaint strokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
StrokeWidth = 3
};
protected SKPaint redStrokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 15
};
protected SKPaint dottedStrokePaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
StrokeWidth = 3,
PathEffect = SKPathEffect.CreateDash(new float[] { 7, 7 }, 0)
};
protected void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = baseCanvasView.CanvasSize.Width / (float)baseCanvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
baseCanvasView.InvalidateSurface();
}
}
}
Die TangentArcPage-Klasse wird von InteractivePage abgeleitet. Der Konstruktor in der TangentArcPage.xaml.cs Datei ist für das Instanziieren und Initialisieren des touchPoints Arrays verantwortlich, und die Einstellung baseCanvasView (in InteractivePage) auf das objekt, das SKCanvasView in der TangentArcPage.xaml-Datei instanziiert wird:
public partial class TangentArcPage : InteractivePage
{
public TangentArcPage()
{
touchPoints = new TouchPoint[3];
for (int i = 0; i < 3; i++)
{
TouchPoint touchPoint = new TouchPoint
{
Center = new SKPoint(i == 0 ? 100 : 500,
i != 2 ? 100 : 500)
};
touchPoints[i] = touchPoint;
}
InitializeComponent();
baseCanvasView = canvasView;
radiusSlider.Value = 100;
}
void sliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Der PaintSurface Handler verwendet die ArcTo Methode, um den Bogen basierend auf den Berührungspunkten und einem Slider, aber auch algorithmisch berechnet den Kreis, auf dem der Winkel basiert:
public partial class TangentArcPage : InteractivePage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw the two lines that meet at an angle
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.LineTo(touchPoints[1].Center);
path.LineTo(touchPoints[2].Center);
canvas.DrawPath(path, dottedStrokePaint);
}
// Draw the circle that the arc wraps around
float radius = (float)radiusSlider.Value;
SKPoint v1 = Normalize(touchPoints[0].Center - touchPoints[1].Center);
SKPoint v2 = Normalize(touchPoints[2].Center - touchPoints[1].Center);
double dotProduct = v1.X * v2.X + v1.Y * v2.Y;
double angleBetween = Math.Acos(dotProduct);
float hypotenuse = radius / (float)Math.Sin(angleBetween / 2);
SKPoint vMid = Normalize(new SKPoint((v1.X + v2.X) / 2, (v1.Y + v2.Y) / 2));
SKPoint center = new SKPoint(touchPoints[1].Center.X + vMid.X * hypotenuse,
touchPoints[1].Center.Y + vMid.Y * hypotenuse);
canvas.DrawCircle(center.X, center.Y, radius, this.strokePaint);
// Draw the tangent arc
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ArcTo(touchPoints[1].Center, touchPoints[2].Center, radius);
canvas.DrawPath(path, redStrokePaint);
}
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
}
Dies ist die Ausgeführte Tangenten arc-Seite :
Der Tangensbogen eignet sich ideal zum Erstellen abgerundeter Ecken, z. B. eines abgerundeten Rechtecks. Da SKPath bereits eine AddRoundedRect Methode enthalten ist, veranschaulicht die Rounded Heptagon-Seite , wie ArcTo die Ecken eines siebenseitigen Polygons gerundet werden. (Der Code wird für ein normales Polygon generalisiert.)
Der PaintSurface Handler der RoundedHeptagonPage Klasse enthält eine for Schleife, um die Koordinaten der sieben Scheitelpunkte des Heptagon zu berechnen, und eine Sekunde, um die Mittelpunkte der sieben Seiten aus diesen Scheitelpunkten zu berechnen. Diese Mittelpunkte werden dann zum Erstellen des Pfads verwendet:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
float cornerRadius = 100;
int numVertices = 7;
float radius = 0.45f * Math.Min(info.Width, info.Height);
SKPoint[] vertices = new SKPoint[numVertices];
SKPoint[] midPoints = new SKPoint[numVertices];
double vertexAngle = -0.5f * Math.PI; // straight up
// Coordinates of the vertices of the polygon
for (int vertex = 0; vertex < numVertices; vertex++)
{
vertices[vertex] = new SKPoint(radius * (float)Math.Cos(vertexAngle),
radius * (float)Math.Sin(vertexAngle));
vertexAngle += 2 * Math.PI / numVertices;
}
// Coordinates of the midpoints of the sides connecting the vertices
for (int vertex = 0; vertex < numVertices; vertex++)
{
int prevVertex = (vertex + numVertices - 1) % numVertices;
midPoints[vertex] = new SKPoint((vertices[prevVertex].X + vertices[vertex].X) / 2,
(vertices[prevVertex].Y + vertices[vertex].Y) / 2);
}
// Create the path
using (SKPath path = new SKPath())
{
// Begin at the first midpoint
path.MoveTo(midPoints[0]);
for (int vertex = 0; vertex < numVertices; vertex++)
{
SKPoint nextMidPoint = midPoints[(vertex + 1) % numVertices];
// Draws a line from the current point, and then the arc
path.ArcTo(vertices[vertex], nextMidPoint, cornerRadius);
// Connect the arc with the next midpoint
path.LineTo(nextMidPoint);
}
path.Close();
// Render the path in the center of the screen
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 10;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.DrawPath(path, paint);
}
}
}
Dies ist das Programm, das ausgeführt wird:
Der elliptische Bogen
Der elliptische Bogen wird einem Pfad mit einem Aufruf der ArcTo Methode mit zwei SKPoint Parametern oder der ArcTo Überladung mit separaten X- und Y-Koordinaten hinzugefügt:
public void ArcTo (SKPoint r, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, SKPoint xy)
public void ArcTo (Single rx, Single ry, Single xAxisRotate, SKPathArcSize largeArc, SKPathDirection sweep, Single x, Single y)
Der elliptische Bogen entspricht dem elliptischen Bogen, der in skalierbaren Vektorgrafiken (SVG) und der Universelle Windows-Plattform ArcSegment Klasse enthalten ist.
Diese ArcTo Methoden zeichnen einen Bogen zwischen zwei Punkten, die den aktuellen Punkt der Kontur und den letzten Parameter für die ArcTo Methode (den xy Parameter oder die separaten x und y Parameter) darstellen:

Der erste Punktparameter für die ArcTo Methode (roder rx und ry) ist überhaupt kein Punkt, sondern gibt stattdessen die horizontalen und vertikalen Radien einer Ellipse an;

Der xAxisRotate Parameter ist die Anzahl der Grad im Uhrzeigersinn, um diese Ellipse zu drehen:

Wenn diese gekippte Ellipse dann so positioniert ist, dass sie die beiden Punkte berührt, werden die Punkte durch zwei verschiedene Bögen verbunden:

Diese beiden Bögen können auf zwei Arten unterschieden werden: Der obere Bogen ist größer als der untere Bogen, und da der Bogen von links nach rechts gezeichnet wird, wird der obere Bogen in eine uhrzeigersinnige Richtung gezeichnet, während der untere Bogen in einer gegen den Uhrzeigersinn gezeichnet wird.
Es ist auch möglich, die Auslassungspunkte zwischen den beiden Punkten auf eine andere Weise zu passen:

Jetzt gibt es einen kleineren Bogen oben, der im Uhrzeigersinn gezeichnet wird, und einen größeren Bogen unten, der gegen den Uhrzeigersinn gezeichnet wird.
Diese beiden Punkte können daher durch einen Bogen verbunden werden, der durch die gekippte Ellipse auf insgesamt vier Arten definiert ist:

Diese vier Bögen werden durch die vier Kombinationen der SKPathArcSize Argumente und SKPathDirection Enumerationstypen der ArcTo Methode unterschieden:
- rot: SKPathArcSize.Large und SKPathDirection.Clockwise
- grün: SKPathArcSize.Small und SKPathDirection.Clockwise
- blau: SKPathArcSize.Small und SKPathDirection.CounterClockwise
- Magenta: SKPathArcSize.Large und SKPathDirection.CounterClockwise
Wenn die gekippte Ellipse nicht groß genug ist, um zwischen den beiden Punkten zu passen, wird sie gleichmäßig skaliert, bis sie groß genug ist. In diesem Fall verbinden nur zwei eindeutige Bögen die beiden Punkte. Diese können mit dem SKPathDirection Parameter unterschieden werden.
Obwohl dieser Ansatz zum Definieren eines Bogens komplex bei der ersten Begegnung ist, ist es der einzige Ansatz, der das Definieren eines Bogens mit einer gedrehten Ellipse ermöglicht, und es ist oft der einfachste Ansatz, wenn Sie Bögen in andere Teile der Kontur integrieren müssen.
Mit der Elliptical Arc-Seite können Sie die beiden Punkte interaktiv und die Größe und Drehung der Ellipse festlegen. Die EllipticalArcPage Klasse wird von InteractivePage, und der PaintSurface Handler in der EllipticalArcPage.xaml.cs CodeBehind-Datei zeichnet die vier Bögen:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
int colorIndex = 0;
SKPoint ellipseSize = new SKPoint((float)xRadiusSlider.Value,
(float)yRadiusSlider.Value);
float rotation = (float)rotationSlider.Value;
foreach (SKPathArcSize arcSize in Enum.GetValues(typeof(SKPathArcSize)))
foreach (SKPathDirection direction in Enum.GetValues(typeof(SKPathDirection)))
{
path.MoveTo(touchPoints[0].Center);
path.ArcTo(ellipseSize, rotation,
arcSize, direction,
touchPoints[1].Center);
strokePaint.Color = colors[colorIndex++];
canvas.DrawPath(path, strokePaint);
path.Reset();
}
}
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Hier wird folgendes ausgeführt:
Die Arc Infinity-Seite verwendet den elliptischen Bogen, um ein Unendlichkeitszeichen zu zeichnen. Das Unendlichkeitszeichen basiert auf zwei Kreisen mit 100 Einheiten getrennt durch 100 Einheiten:

Zwei linienüberquerende Linien sind tangens für beide Kreise:
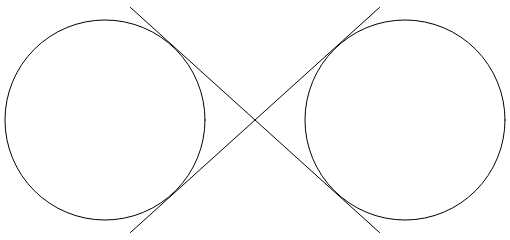
Das Unendlichkeitszeichen ist eine Kombination aus Teilen dieser Kreise und den beiden Linien. Um den elliptischen Bogen zu verwenden, um das Unendlichkeitszeichen zu zeichnen, müssen die Koordinaten bestimmt werden, in denen die beiden Linien tangens zu den Kreisen sind.
Erstellen Sie ein rechtes Rechteck in einem der Kreise:

Der Radius des Kreises beträgt 100 Einheiten, und die Hypotenuse des Dreiecks beträgt 150 Einheiten, sodass der Winkel α der Arkussinus (umgekehrter Sinus) von 100 dividiert durch 150 oder 41,8 Grad ist. Die Länge der anderen Seite des Dreiecks beträgt 150 Mal den Kosinus von 41,8 Grad oder 112, die auch vom Pythagorischen Theorem berechnet werden kann.
Die Koordinaten des Tangenspunkts können dann anhand dieser Informationen berechnet werden:
x = 112·cos(41.8) = 83
y = 112·sin(41.8) = 75
Die vier Tangenspunkte sind alle, die erforderlich sind, um ein Unendlichkeitszeichen zu zeichnen, das auf dem Punkt (0, 0) mit Kreisradien von 100 zentriert ist:

Der PaintSurface Handler in der ArcInfinityPage Klasse positioniert das Unendlichkeitszeichen so, dass der Punkt (0, 0) in der Mitte der Seite positioniert wird, und skaliert den Pfad zur Bildschirmgröße:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.LineTo(83, 75);
path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.CounterClockwise, 83, -75);
path.LineTo(-83, 75);
path.ArcTo(100, 100, 0, SKPathArcSize.Large, SKPathDirection.Clockwise, -83, -75);
path.Close();
// Use path.TightBounds for coordinates without control points
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
Der Code verwendet die Bounds Eigenschaft, SKPath um die Dimensionen des Unendlichen Sinus zu bestimmen, um sie auf die Größe des Zeichenbereichs zu skalieren:
Das Ergebnis scheint ein wenig klein zu sein, was darauf hindeutet, dass die Bounds Eigenschaft SKPath eine Größe meldet, die größer als der Pfad ist.
Intern nähert Skia den Bogen mit mehreren quadratischen Bézierkurven an. Diese Kurven (wie sie im nächsten Abschnitt angezeigt werden) enthalten Kontrollpunkte, die steuern, wie die Kurve gezeichnet wird, aber nicht Teil der gerenderten Kurve sind. Die Bounds Eigenschaft enthält diese Kontrollpunkte.
Um eine engere Anpassung zu erhalten, verwenden Sie die TightBounds Eigenschaft, die die Kontrollpunkte ausschließt. Hier sehen Sie das Programm, das im Querformatmodus ausgeführt wird, und verwenden Sie die TightBounds Eigenschaft, um die Pfadgrenzen abzurufen:
Obwohl die Verbindungen zwischen den Bögen und geraden Linien mathematisch glatt sind, kann der Wechsel von Bogen zu gerade Linie etwas abrupt erscheinen. Im nächsten Artikel zu drei Arten von Bézierkurven wird ein besseres Unendlichkeitszeichen vorgestellt.







