Hinweis
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, sich anzumelden oder das Verzeichnis zu wechseln.
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, das Verzeichnis zu wechseln.
Dieser Artikel konzentriert sich auf die Deep Learning-Methoden für Zeitreihenvorhersagen mit automatisiertem maschinellem Lernen. Anweisungen und Beispiele zum Trainieren von Vorhersagemodellen in AutoML finden Sie in unserem Artikel Einrichten von AutoML für Zeitreihenvorhersagen.
Für Deep Learning gibt es zahlreiche Anwendungsfälle in verschiedensten Bereiche – von der Sprachmodellierung bis hin zur Proteinfaltung. Zeitreihenvorhersagen profitieren ebenfalls von den jüngsten Fortschritten bei der Deep Learning-Technologie. Beispielsweise zählen DNN-Modelle (Deep Neural Network) in der vierten und fünften Iteration des hochkarätigen Makridakis-Vorhersagewettbewerbs zu den leistungsstärksten Modellen.
In diesem Artikel werden die Struktur und der Betrieb des TCNForecaster-Modells im automatisierten maschinellen Lernen beschrieben, damit Sie das Modell bestmöglich auf Ihr Szenario anwenden können.
Einführung in TCNForecaster
TCNForecaster ist ein temporales Faltungsnetzwerk (Temporal Convolutional Network, TCN) mit einer für Zeitreihendaten konzipierten DNN-Architektur. Das Modell verwendet historische Daten für eine Zielmenge sowie zugehörige Features, um probabilistische Vorhersagen des Ziels bis zu einem angegebenen Vorhersagehorizont zu generieren. Die folgende Abbildung zeigt die Hauptkomponenten der TCNForecaster-Architektur:
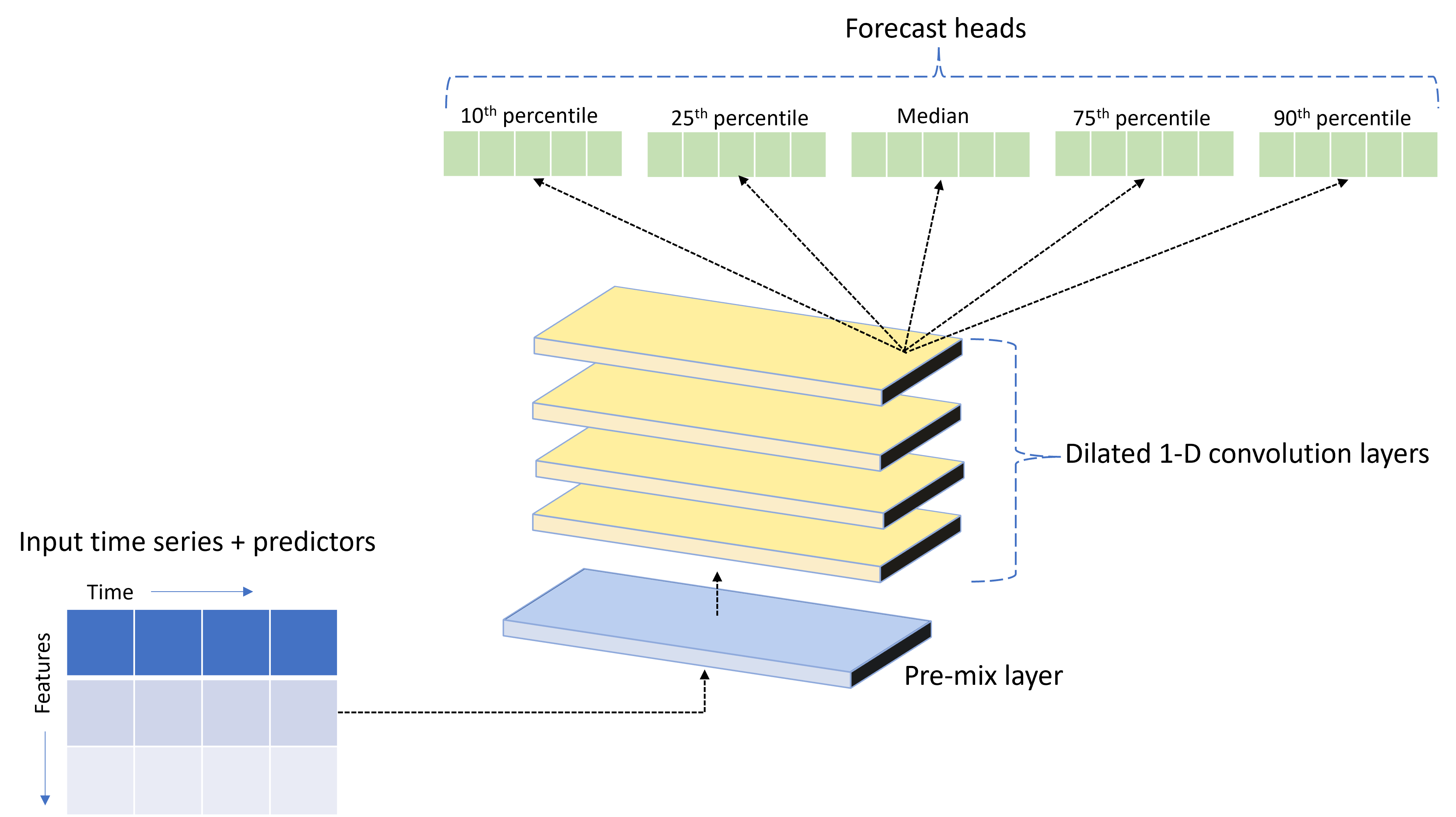
TCNForecaster umfasst folgende Hauptkomponenten:
- Eine Mischvorbereitungsebene, auf der die Eingabezeitreihen und Featuredaten zu einem Array von Signalkanälen gemischt werden, das dann vom Faltungsstapel verarbeitet wird.
- Einen Stapel erweiterter Faltungsebenen, der das Kanalarray sequenziell verarbeitet. Jede Ebene im Stapel verarbeitet die Ausgabe der vorherigen Ebene, um ein neues Kanalarray zu erzeugen. Jeder Kanal in dieser Ausgabe enthält eine Mischung aus faltungsgefilterten Signalen von den Eingangskanälen.
- Eine Sammlung von Vorhersagehaupteinheiten, die die Ausgangssignale der Faltungsebenen zusammenführen und die Zielmenge auf der Grundlage dieser latenten Darstellung vorhersagen. Jede Haupteinheit erzeugt Vorhersagen für ein Quantil der Vorhersageverteilung bis zum Horizont.
Erweiterte kausale Faltung
Der zentrale Vorgang eines TCN ist eine erweiterte kausale Faltung entlang der Zeitdimension eines Eingangssignals. Die Faltung mischt intuitiv Werte nahe gelegener Zeitpunkte in der Eingabe. Bei den Proportionen in der Mischung handelt es sich um den Kern (oder um die Gewichtungen) der Faltung. Die Trennung zwischen Punkten in der Mischung ist dagegen die Erweiterung. Das Ausgangssignal wird auf der Grundlage der Eingabe generiert. Hierzu wird der Kern zeitlich entlang der Eingabe bewegt und die Mischung an jeder Position akkumuliert. Bei einer kausalen Faltung werden vom Kern nur Eingabewerte aus der Vergangenheit in Relation zu den einzelnen Ausgabepunkten gemischt, sodass die Ausgabe nicht in die Zukunft gerichtet ist.
Durch Stapeln erweiterter Faltungen kann das TCN Korrelationen über lange Zeiträume in Eingabesignalen mit relativ wenig Kerngewichtungen modellieren. Die folgende Abbildung zeigt beispielsweise drei gestapelte Ebenen mit einem Kernel mit zwei Gewichtungen pro Ebene und exponentiell zunehmenden Erweiterungsfaktoren:

Die gestrichelten Linien zeigen Pfade durch das Netzwerk an, die bei der Ausgabe zur Zeit $t$ enden. Diese Pfade decken die letzten acht Punkte in der Eingabe ab und veranschaulichen, dass jeder Ausgabepunkt eine Funktion der acht relativ neuesten Punkte in der Eingabe ist. Die Länge des Verlaufs oder Rückblicks, den ein Faltungsnetzwerk verwendet, um Vorhersagen zu treffen, wird als rezeptives Feld bezeichnet und vollständig von der TCN-Architektur bestimmt.
TCNForecaster-Architektur
Das Herzstück der TCNForecaster-Architektur ist der Stapel von Faltungsschichten zwischen der Mischvorbereitung und den Vorhersagehaupteinheiten. Der Stapel wird logisch in Wiederholungseinheiten (sogenannte Blöcke) unterteilt, die sich wiederum aus residualen Zellen zusammensetzen. Eine residuale Zelle wendet kausale Faltungen mit einer festgelegten Erweiterung an – zusammen mit Normalisierung und nichtlinearer Aktivierung. Wichtig ist, dass jede residuale Zelle ihre Ausgabe über eine sogenannte residuale Verbindung zu ihrer Eingabe hinzufügt. Diese Verbindungen haben nachweislich Vorteile für das DNN-Training – vielleicht, weil sie einen effizienteren Informationsfluss durch das Netzwerk ermöglichen. Die folgende Abbildung zeigt die Architektur der Faltungsebenen für ein Beispielnetzwerk mit zwei Blöcken und drei residualen Zellen in jedem Block:

Die Anzahl von Blöcken und Zellen sowie die Anzahl von Signalkanälen auf jeder Ebene steuern die Größe des Netzwerks. Die Architekturparameter von TCNForecaster sind in der folgenden Tabelle zusammengefasst:
| Parameter | BESCHREIBUNG |
|---|---|
| $n_{b}$ | Anzahl von Blöcken im Netzwerk (Tiefe) |
| $n_{c}$ | Anzahl von Zellen in jedem Block |
| $n_{\text{ch}}$ | Anzahl von Kanälen auf den verborgenen Ebenen |
Das rezeptive Feld hängt von den Tiefenparametern ab und wird durch folgende Formel angegeben:
$t_{\text{rf}} = 4n_{b}\left(2^{n_{c}} - 1\right) + 1.$
Mithilfe von Formeln können wir eine präzisere Definition der TCNForecaster-Architektur bereitstellen. $X$ sei ein Eingabearray, in dem jede Zeile Featurewerte aus den Eingabedaten enthält. $X$ kann in numerische und kategorische Featurearrays ($X_{\text{num}}$ und $X_{\text{cat}}$) unterteilt werden. Dann wird TCNForecaster durch folgende Formeln angegeben:
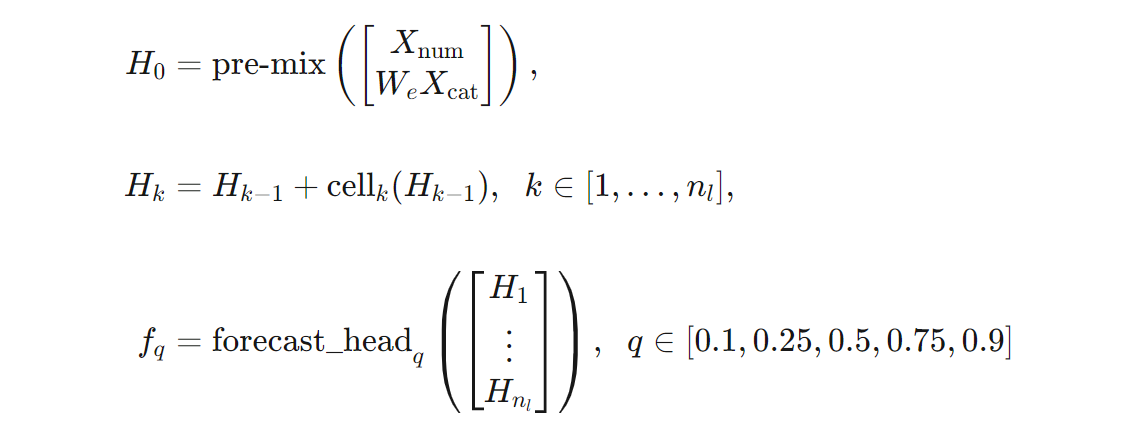
Hierbei ist $W_{e}$ eine Einbettungsmatrix für die kategorischen Features, $n_{l} = n_{b}n_{c}$ ist die Gesamtanzahl residualer Zellen, $H_{k}$ steht für die Ausgaben verborgener Ebenen, und $f_{q}$ sind Vorhersageausgaben für bestimmte Quantile der Vorhersageverteilung. Zum besseren Verständnis sind die Dimensionen dieser Variablen in der folgenden Tabelle zusammengefasst:
| Variable | BESCHREIBUNG | Dimensionen |
|---|---|---|
| $X$ | Eingabearray | $n_{\text{input}} \times t_{\text{rf}}$ |
| $H_{i}$ | Ausgabe verborgener Ebenen für $i=0,1,\ldots,n_{l}$ | $n_{\text{ch}} \times t_{\text{rf}}$ |
| $f_{q}$ | Vorhersageausgabe für das Quantil $q$ | $h$ |
In der Tabelle gilt: $n_{\text{input}} = n_{\text{features}} + 1$ (also Anzahl von Prädiktor-/Featurevariablen plus Zielmenge). Die Vorhersagehaupteinheiten generieren alle Vorhersagen bis zum maximalen Horizont ($h$) in einem einzelnen Durchgang. Bei TCNForecaster handelt es sich also um eine direkte Vorhersage.
TCNForecaster im automatisierten maschinellen Lernen
TCNForecaster ist ein optionales Modell im automatisierten maschinellen Lernen. Informationen zur Verwendung finden Sie unter Aktivieren von Deep Learning.
In diesem Abschnitt erfahren Sie, wie automatisiertes maschinelles Lernen TCNForecaster-Modelle mit Ihren Daten erstellt, und Sie erhalten Informationen zur Datenvorverarbeitung, zum Training und zur Modellsuche.
Schritte zur Vorverarbeitung der Daten
Automatisiertes maschinelles Lernen führt mehrere Vorverarbeitungsschritte für Ihre Daten aus, um sie für das Modelltraining aufzubereiten. In der folgenden Tabelle werden diese Schritte in der Reihenfolge beschrieben, in der sie ausgeführt werden:
| Schritt | BESCHREIBUNG |
|---|---|
| Auffüllen fehlender Daten | Ergänzen fehlender Werte und Beobachtungslücken durch Imputation und optional Auffüllen oder Löschen kurzer Zeitreihen |
| Erstellen von Kalenderfeatures | Erweitern Sie die Eingabedaten mit abgeleiteten Kalenderfeatures wie dem Wochentag und optional mit Feiertagen für eine bestimmte Region oder ein bestimmtes Land. |
| Codieren kategorischer Daten | Versehen Sie Zeichenfolgen und andere kategorische Typen (einschließlich aller Zeitreihen-ID-Spalten) mit einer Beschriftungscodierung. |
| Zieltransformation | Wenden Sie optional die natürliche Logarithmusfunktion auf das Ziel an (abhängig von den Ergebnissen bestimmter statistischer Tests). |
| Normalisierung | Führen Sie eine Z-Wert-Normalisierung für alle numerischen Daten durch. Die Normalisierung erfolgt pro Feature und Zeitreihengruppe, wie durch die Spalten der Zeitreihen-ID-Spalten definiert. |
Diese Schritte sind in den Transformationspipelines des automatisierten maschinellen Lernens enthalten, sodass sie bei Bedarf automatisch zur Rückschlusszeit angewendet werden. In einigen Fällen ist der umgekehrte Vorgang zu einem Schritt in der Rückschlusspipeline enthalten. Wenn das automatisierte maschinelle Lernen beispielsweise beim Training eine $\log$-Transformation auf das Ziel angewendet hat, werden die Rohvorhersagen in der Rückschlusspipeline potenziert.
Ausbildung
TCNForecaster verwendet bewährte DNN-Trainingsmethoden, die für andere Anwendungen in Bildern und Sprache üblich sind. Das automatisierte maschinelle Lernen unterteilt vorverarbeitete Trainingsdaten in Beispiele, die gemischt und zu Batches kombiniert werden. Das Netzwerk verarbeitet die Batches sequenziell unter Verwendung von Backpropagation und stochastischem Gradientenverfahren, um die Netzwerkgewichtungen in Bezug auf eine Verlustfunktion zu optimieren. Das Training kann viele Durchläufe durch die vollständigen Trainingsdaten erfordern. Die einzelnen Durchgänge werden jeweils als Epoche bezeichnet.
In der folgenden Tabelle werden Eingabeeinstellungen und Parameter für das TCNForecaster-Training aufgeführt und beschrieben:
| Trainingseingabe | BESCHREIBUNG | Wert |
|---|---|---|
| Validierungsdaten | Ein Teil der Daten, der nicht zum Trainieren verwendet wird, um die Netzwerkoptimierung zu steuern und eine Überanpassung zu verringern. | Vom Benutzer bereitgestellt oder automatisch aus Trainingsdaten erstellt, falls nicht bereitgestellt |
| Primary metric (Primäre Metrik) | Metrik, die aus Medianwertvorhersagen für die Validierungsdaten am Ende jeder Trainingsepoche berechnet wird. Wird für vorzeitiges Beenden und Modellauswahl verwendet. | Vom Benutzer ausgewählt. Normalisierte mittlere quadratische Gesamtabweichung oder normalisierte mittlere absolute Abweichung. |
| Trainingsepochen | Maximale Anzahl von Epochen, die für die Optimierung der Netzwerkgewichtung ausgeführt werden sollen. | 100. Training kann durch Logik für automatisiertes vorzeitiges Beenden bei einer geringeren Anzahl von Epochen beendet werden. |
| Wartezeit für vorzeitiges Beenden | Gibt an, wie viele Epochen auf die Verbesserung der primären Metrik gewartet werden soll, bevor das Training beendet wird. | 20 |
| Verlustfunktion | Die Zielfunktion für die Optimierung der Netzwerkgewichtung. | Quantilverlust als Durchschnittswert für die Vorhersagen des 10., 25., 50., 75. und 90. Perzentils. |
| Batchgröße | Anzahl von Beispielen in einem Batch. Jedes Beispiel verfügt über die Dimensionen $n_{\text{input}} \times t_{\text{rf}}$ für die Eingabe und $h$ für die Ausgabe. | Wird automatisch anhand der Gesamtzahl von Beispielen in den Trainingsdaten bestimmt. Höchstwert: 1.024. |
| Einbettungsdimensionen | Dimensionen der Einbettungsräume für kategorische Features. | Wird automatisch auf die vierte Wurzel der Anzahl unterschiedlicher Werte in jedem Feature festgelegt und auf die nächste ganze Zahl aufgerundet. Schwellenwerte werden bei einem Mindestwert von 3 und bei einem Höchstwert von 100 angewendet. |
| Netzwerkarchitektur* | Parameter, die die Größe und Form des Netzwerks steuern: Tiefe, Anzahl von Zellen und Anzahl von Kanälen. | Bestimmt durch die Modellsuche. |
| Netzwerkgewichtungen | Parameter, die Signalmischungen, kategorische Einbettungen, Faltungskerngewichtungen und Zuordnungen zu Vorhersagewerten steuern. | Zufällig initialisiert, dann in Bezug auf die Verlustfunktion optimiert. |
| Lernrate* | Steuert, wie stark die Netzwerkgewichtungen bei jeder Iteration des Gradientenabstiegs angepasst werden können. Wird nahe der Konvergenz dynamisch verringert. | Bestimmt durch die Modellsuche. |
| Dropout-Verhältnis* | Steuert den Grad der angewendeten Dropout-Abgrenzung für die Netzwerkgewichtungen. | Bestimmt durch die Modellsuche. |
Mit einem Sternchen (*) gekennzeichnete Eingaben werden durch eine Hyperparametersuche bestimmt, die im nächsten Abschnitt beschrieben wird.
Modellsuche
Automatisiertes maschinelles Lernen verwendet Modellsuchmethoden, um Werte für die folgenden Hyperparameter zu finden:
- Netzwerktiefe oder Anzahl von Faltungsblöcken
- Anzahl von Zellen pro Block
- Anzahl von Kanälen auf den einzelnen verborgenen Ebenen
- Dropout-Verhältnis für die Netzwerkabgrenzung
- Lernrate
Optimale Werte für diese Parameter können je nach Problemszenario und Trainingsdaten erheblich variieren, sodass automatisiertes maschinelles Lernen mehrere verschiedene Modelle innerhalb des Bereichs von Hyperparameterwerten trainiert und das beste Modell (gemäß Bewertung der primären Metrik für die Validierungsdaten) auswählt.
Die Modellsuche umfasst zwei Phasen:
- Das automatisierte maschinelle Lernen führt eine Suche mit 12 „Orientierungsmodellen“ durch. Die Orientierungsmodelle sind statisch und decken den Hyperparameterraum angemessen ab.
- Das automatisierte maschinelle Lernen setzt die Suche im Hyperparameterraum mit einer zufallsbasierten Suche fort.
Die Suche wird beendet, wenn die Beendigungskriterien erfüllt sind. Die Beendigungskriterien hängen von der Konfiguration des Trainingsauftrags für die Vorhersage ab. Beispiele sind etwa Zeitlimits, Grenzwerte für die Anzahl durchzuführender Suchtests und die Logik für vorzeitiges Beenden, wenn sich die Validierungsmetrik nicht verbessert.
Nächste Schritte
- Informieren Sie sich über das Einrichten von automatisiertem maschinellem Lernen zum Trainieren eines Zeitreihenvorhersagemodells.
- Machen Sie sich mit Vorhersagemethoden in automatisiertem maschinellem Lernen vertraut.
- Sehen Sie sich häufig gestellte Fragen zu Vorhersagen in automatisiertem maschinellem Lernen an.