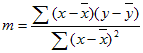WorksheetFunction.LinEst-Methode (Excel)

Berechnet die Statistiken für eine Linie mithilfe der Methode der kleinsten Quadrate, um eine gerade Linie zu berechnen, die am besten zu Ihren Daten passt, und gibt ein Array zurück, das die Linie beschreibt. Da diese Funktion einen Array von Werten zurückgibt, muss sie als Arrayformel eingegeben werden.

Syntax

Ausdruck. LinEst (Arg1, Arg2, Arg3, Arg4)

Ausdruck Eine Variable, die ein WorksheetFunction-Objekt darstellt.

Parameter

Name	Erforderlich/Optional	Datentyp	Beschreibung
Arg1	Erforderlich	Variant	Known_y - die Gruppe von y-Werten, die Sie bereits in der Beziehung y = mx + b kennen.
Arg2	Optional	Variant	X_Werte - eine optionale Menge mit möglicherweise bereits bekannten x-Werten in der Beziehung y = mx + b.
Arg3	Optional	Variant	Konstante - ein Wahrheitswert, mit dem angegeben wird, ob erzwungen werden soll, dass die Konstante b gleich 0 sein soll.
Arg4	Optional	Variant	Stats - ein Wahrheitswert, der angibt, ob weitere Regressionskenngrößen zurückgegeben werden sollen.

Rückgabewert

Variant

Bemerkungen

Die Gleichung für die Zeile lautet y = mx + b oder y = m1x1 + m2x2 + ... + b (wenn mehrere Bereiche von x-Werten vorhanden sind), wobei der abhängige y-Wert eine Funktion der unabhängigen x-Werte ist. Die m-Werte sind Koeffizienten, die zu den jeweiligen x-Werten gehören, und b ist eine Konstante. Es ist zu beachten, dass y, x und m Vektoren sein können. Das Von LinEst zurückgegebene Array ist {mn,mn-1,...,m1,b}. LinEst kann auch zusätzliche Regressionsstatistiken zurückgeben.

Wenn sich das Array known_y in einer einzelnen Spalte befindet, wird jede Spalte von known_x als separate Variable interpretiert.

Wenn sich das Array known_y in einer einzelnen Zeile befindet, wird jede Zeile von known_x als separate Variable interpretiert.

Das Array Bekannt_x kann eine oder mehrere Gruppen mit Variablen enthalten. Wenn nur eine Variable verwendet wird, können Bekannt_y und Bekannt_x Bereiche beliebiger Form darstellen, solange sie gleiche Abmessungen aufweisen. Wenn mehrere Variablen verwendet werden, muss Bekannt_y einen Vektor darstellen (d. h. einen Bereich mit einer Höhe von einer Zeile oder einer Breite von einer Spalte).

Wenn known_x nicht angegeben wird, wird davon ausgegangen, dass es sich um das Array {1,2,3,...} handelt, das die gleiche Größe wie known_y hat.

• Wenn const auf True festgelegt oder nicht angegeben ist, wird b normal berechnet.

• Wenn const auf False festgelegt ist, wird b gleich 0 festgelegt, und die m-Werte werden so angepasst, dass sie passen y = mx.

• Wenn stats auf True festgelegt ist, gibt LinEst die zusätzliche Regressionsstatistik zurück, sodass das zurückgegebene Array ist {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}.

• Wenn stats den Wert False aufweist oder ausgelassen wird, gibt LinEst nur die m-Koeffizienten und die Konstante b zurück.

Die folgenden Regressionskenngrößen können zusätzlich ermittelt werden:

Regressionsstatistik	Beschreibung
se1,se2,...,sen	Sind die Standardfehlerwerte der Koeffizienten m1;m2;...;mn.
seb	Der Standardfehlerwert für die Konstante b (seb = #N/A, wenn const auf False festgelegt ist).
R2	Der Bestimmungskoeffizient. Vergleicht geschätzte und tatsächliche y-Werte und Wertebereiche von 0 bis 1. Wenn es 1 ist, gibt es eine perfekte Korrelation in der Stichprobe – es gibt keinen Unterschied zwischen dem geschätzten y-Wert und dem tatsächlichen y-Wert. Wenn der Bestimmungskoeffizient 0 ist, ist die Regressionsgleichung bei der Vorhersage eines y-Werts nicht hilfreich.
sey	Der Standardfehler des Schätzwerts y (Prognosewert).
F	Die F-Statistik (oder der berechnete F-Wert). Anhand der F-Statistik können Sie entscheiden, ob die zwischen der abhängigen und der unabhängigen Variablen beobachtete Beziehung zufällig ist oder nicht.
df	Die Anzahl der Freiheitsgrade. Mit den Freiheitsgraden können Sie den jeweiligen kritischen F-Wert (Quantil F) aus einer entsprechenden statistischen Tabelle entnehmen. Vergleichen Sie die Werte, die Sie in der Tabelle finden, mit der von LinEst zurückgegebenen F-Statistik, um ein Konfidenzniveau für das Modell zu ermitteln.
ssreg	Die Regressionssumme der Quadrate.
ssresid	Die Residualsumme der Quadrate.

Die folgende Abbildung zeigt, in welcher Reihenfolge die zusätzlichen Regressionskenngrößen zurückgegeben werden.

Sie können jede gerade Linie mit der Steigung und dem y-Abschnitt beschreiben: Slope (m). Um die Steigung einer Linie zu finden, die häufig als m geschrieben wird, nehmen Sie zwei Punkte auf der Linie, (x1,y1) und (x2,y2); die Steigung ist gleich (y2 - y1)/(x2 - x1). Y-Intercept (b): Der y-Schnittpunkt einer Linie, der häufig als b geschrieben wird, ist der Wert von y an dem Punkt, an dem die Linie die y-Achse kreuzt. Die Gleichung einer geraden Linie lautet y = mx + b. Nachdem Sie die Werte von m und b kennen, können Sie einen beliebigen Punkt in der Linie berechnen, indem Sie den y- oder x-Wert in diese Gleichung einfügen. Sie können auch die TREND-Funktion verwenden.

Wenn Sie nur über eine unabhängige x-Variable verfügen, können Sie die Steigungs- und y-Intercept-Werte direkt mithilfe der folgenden Formeln abrufen:

• Steigung: =INDEX(LINEST(known_y's,known_x's),1)
• Y-Intercept: =INDEX(LINEST(known_y's,known_x's),2)

Die Genauigkeit der von LinEst berechneten Linie hängt vom Grad der Streuung in Ihren Daten ab. Je linearer die Daten sind, desto genauer ist das LinEst-Modell . LinEst verwendet die Methode der kleinsten Quadrate, um die beste Eignung für die Daten zu bestimmen. Wenn nur eine unabhängige x-Variable vorliegt, werden m und b entsprechend der folgenden Formeln berechnet:

, wobei x und y Stichprobenmittel sind, d. h. x = MITTELWERT (bekannte x)-Werte und y = MITTELWERT(known_y).

Die Linien- und Kurvenanpassungsfunktionen LinEst und LogEst können die beste gerade Linie oder exponentielle Kurve berechnen, die zu Ihren Daten passt. Sie müssen dennoch entscheiden, welches der beiden Ergebnisse Ihren Daten eher entspricht. Sie können für eine gerade Linie oder GROWTH(known_y's, known_x's) für eine exponentielle Kurve berechnenTREND(known_y's,known_x's). Werden diese Funktionen ohne das Argument Neue_X_Werte verwendet, geben sie ein Array mit y-Werten zurück, die an den x-Werten Ihrer tatsächlichen Datenpunkte als Vorhersagewerte auf der Geraden oder Exponentialkurve liegen. Diese Vorhersagewerte können Sie mit den tatsächlichen Werten vergleichen. Um eine bessere Vergleichsmöglichkeit zu haben, kann es sinnvoll sein, die Werte in Diagrammen darzustellen.

In der Regressionsanalyse berechnet Microsoft Excel für jeden Punkt die quadratische Differenz zwischen dem für diesen Punkt geschätzten y-Wert und seinem tatsächlichen y-Wert. Die Summe dieser quadrierten Differenzen wird als Residual-Quadratsumme (ssresid) bezeichnet. Excel berechnet dann die Gesamtsumme der Quadrate( sstotal). Ist Konstante mit TRUE belegt oder nicht angegeben, entspricht die Gesamtsumme der Abweichungsquadrate der Summe der quadratischen Differenzen zwischen den tatsächlichen y-Werten und dem Mittelwert der y-Werte. Wenn Konstante mit FALSE belegt ist, entspricht die Gesamtsumme der Abweichungsquadrate den Quadraten der tatsächlichen y-Werte (ohne Subtraktion der Mittelwerte aller y-Werte von jedem einzelnen y-Wert). Dann kann die Regressionssumme der Quadrate, ssreg, in ssreg = sstotal - ssresidgefunden werden. Je kleiner die Restsumme der Quadrate im Vergleich zur Gesamtsumme der Quadrate ist, desto größer ist der Wert des Bestimmungskoeffizienten r2, der ein Indikator dafür ist, wie gut die Gleichung, die sich aus der Regressionsanalyse ergibt, die Beziehung zwischen den Variablen erklärt; r2 entspricht ssreg/sstotal.

In einigen Fällen hat eine oder mehrere der X-Spalten (angenommen, dass Y- und X-Spalten in Spalten enthalten sind) möglicherweise keinen zusätzlichen Vorhersagewert, wenn die anderen X-Spalten vorhanden sind. Anders ausgedrückt: Das Entfernen einer oder mehrerer X-Spalten kann zu vorhergesagten Y-Werten führen, die genauso genau sind. In diesem Fall sollten diese redundanten X-Spalten aus dem Regressionsmodell weggelassen werden. Dieses Phänomen wird als Kollinearität bezeichnet, da jede redundante X-Spalte als Summe von Vielfachen der nicht redundanten X-Spalten ausgedrückt werden kann. LinEst überprüft auf Kollinearität und entfernt alle redundanten X-Spalten aus dem Regressionsmodell, wenn sie identifiziert werden. Entfernte X-Spalten können in der LinEst-Ausgabe als Koeffizienten von 0 und 0 se erkannt werden.

• Wenn eine oder mehrere Spalten als redundant entfernt werden, ist df betroffen, da df von der Anzahl der X-Spalten abhängt, die tatsächlich für Vorhersagezwecke verwendet werden. Wenn df geändert wird, weil redundante X-Spalten entfernt werden, sind auch die Werte sey und F betroffen.
• Kollinearität sollte in der Praxis relativ selten sein. Ein Fall, in dem es wahrscheinlicher ist, ist, dass einige X-Spalten nur 0 und 1 als Indikatoren dafür enthalten, ob ein Subjekt in einem Experiment Mitglied einer bestimmten Gruppe ist oder nicht. Wenn const = TRUE oder ausgelassen wird, fügt LinEst effektiv eine zusätzliche X-Spalte aller 1 ein, um den Intercept zu modellieren. Wenn Sie über eine Spalte mit einer 1 für jedes Thema verfügen, wenn sie männlich ist, oder 0, wenn nicht, und Sie haben auch eine Spalte mit einer 1 für jeden Betreff, falls weiblich, oder 0, wenn nicht, ist diese zweite Spalte redundant, da die Einträge darin durch Subtrahieren des Eintrags in der männlichen Indikatorspalte vom Eintrag in der zusätzlichen Spalte aller von LinEst hinzugefügten 1 erhalten werden können.
• df wird wie folgt berechnet, wenn keine X-Spalten aufgrund von Kollinearität aus dem Modell entfernt werden: wenn es k Spalten mit known_x und const = TRUE oder ausgelassen gibt, df = n - k - 1. Wenn const = FALSE, df = n - k. In beiden Fällen erhöht sich jede X-Spalte, die aufgrund von Kollinearität entfernt wurde, df um 1.

Formeln, die Arrays zurückgeben, müssen als Arrayformeln eingegeben werden.

• When entering an array constant such as known_x's as an argument, use commas to separate values in the same row and semicolons to separate rows. Trennzeichen können je nach Gebietsschemaeinstellung in den Optionen "Region" und "Sprache" in Systemsteuerung unterschiedlich sein.
• Beachten Sie, dass mithilfe einer Regressionsformel vorhergesagte y-Werte möglicherweise ungültig sind, wenn diese außerhalb des Bereichs der y-Werte liegen, die Sie zur Ermittlung der Formel verwendet haben.

Der zugrunde liegende Algorithmus, der in der LinEst-Funktion verwendet wird, unterscheidet sich von dem zugrunde liegenden Algorithmus, der in den Funktionen Steigung und Abfangen verwendet wird. Bei unbestimmten und kollinearen Daten kann der Unterschied zwischen diesen Algorithmen zu unterschiedlichen Ergebnissen führen. Wenn beispielsweise die Datenpunkte in Y_Werte den Wert 0 und die Datenpunkte in X_Werte den Wert 1 aufweisen, geschieht Folgendes:

• LinEst gibt den Wert 0 zurück. Der LinEst-Algorithmus ist so konzipiert, dass er vernünftige Ergebnisse für kollineare Daten zurückgibt. In diesem Fall kann mindestens eine Antwort gefunden werden.
• Steigung und Intercept geben einen #DIV/0 zurück! zurück. Der Algorithmus "Slope and Intercept " ist so konzipiert, dass er nach nur einer Antwort sucht, und in diesem Fall kann es mehrere Antworten geben.

Support und Feedback

Haben Sie Fragen oder Feedback zu Office VBA oder zu dieser Dokumentation? Unter Office VBA-Support und Feedback finden Sie Hilfestellung zu den Möglichkeiten, wie Sie Support erhalten und Feedback abgeben können.