Hinweis
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, sich anzumelden oder das Verzeichnis zu wechseln.
Für den Zugriff auf diese Seite ist eine Autorisierung erforderlich. Sie können versuchen, das Verzeichnis zu wechseln.
Tauchen Sie tiefer in SkiaSharp-Transformationen mit der vielseitigen Transformationsmatrix ein
Alle transformationen, die auf das SKCanvas Objekt angewendet werden, werden in einer einzigen Instanz der SKMatrix Struktur konsolidiert. Dies ist eine standardmäßige 3:3-Transformationsmatrix, die denen in allen modernen 2D-Grafiksystemen ähnelt.
Wie Sie gesehen haben, können Sie Transformationen in SkiaSharp verwenden, ohne sich über die Transformationsmatrix zu informieren, aber die Transformationsmatrix ist aus theoretischer Sicht wichtig, und es ist entscheidend, wenn Sie Transformationen zum Ändern von Pfaden oder für die Behandlung komplexer Toucheingaben verwenden, die beide in diesem Artikel und im nächsten Thema veranschaulicht werden.

Die aktuelle Transformationsmatrix, die auf die SKCanvas Transformation angewendet wird, ist jederzeit verfügbar, indem Sie auf die schreibgeschützte TotalMatrix Eigenschaft zugreifen. Sie können eine neue Transformationsmatrix mithilfe der SetMatrix Methode festlegen und diese Transformationsmatrix durch Aufrufen von ResetMatrixStandardwerten wiederherstellen.
Das einzige andere SKCanvas Element, das direkt mit der Matrixtransformation des Zeichenbereichs arbeitet, besteht Concat darin, dass zwei Matrizen miteinander verkettet werden, indem sie miteinander multipliziert werden.
Die Standardtransformationsmatrix ist die Identitätsmatrix und besteht aus 1 in den diagonalen Zellen und 0 an allen anderen Stellen:
| 1 0 0 | | 0 1 0 | | 0 0 1 |
Sie können eine Identitätsmatrix mit der statischen SKMatrix.MakeIdentity Methode erstellen:
SKMatrix matrix = SKMatrix.MakeIdentity();
Der SKMatrix Standardkonstruktor gibt keine Identitätsmatrix zurück. Sie gibt eine Matrix zurück, in der alle Zellen auf Null festgelegt sind. Verwenden Sie den SKMatrix Konstruktor nur, wenn Sie diese Zellen manuell festlegen möchten.
Wenn SkiaSharp ein grafisches Objekt rendert, wird jeder Punkt (x, y) effektiv in eine 1:3-Matrix mit einer 1 in der dritten Spalte konvertiert:
| x y 1 |
Diese 1:3-Matrix stellt einen dreidimensionalen Punkt dar, wobei die Z-Koordinate auf 1 festgelegt ist. Es gibt mathematische Gründe (später erläutert), warum eine zweidimensionale Matrixtransformation drei Dimensionen erfordert. Sie können sich diese 1:3-Matrix als Darstellung eines Punkts in einem 3D-Koordinatensystem vorstellen, aber immer auf der 2D-Ebene, wobei Z gleich 1 ist.
Diese 1:3-Matrix wird dann mit der Transformationsmatrix multipliziert, und das Ergebnis ist der auf dem Zeichenbereich gerenderte Punkt:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Bei Verwendung der Standardmäßigen Matrixmultiplikation sind die konvertierten Punkte wie folgt:
x' = x
y' = y
z' = 1
Dies ist die Standardtransformation.
Wenn die Translate Methode für das SKCanvas Objekt aufgerufen wird, werden die tx Argumente und ty Argumente für die Translate Methode zu den ersten beiden Zellen in der dritten Zeile der Transformationsmatrix:
| 1 0 0 | | 0 1 0 | | tx ty 1 |
Die Multiplikation ist jetzt wie folgt:
| 1 0 0 |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| tx ty 1 |
Hier sind die Transformationsformeln:
x' = x + tx
y' = y + ty
Skalierungsfaktoren weisen den Standardwert 1 auf. Wenn Sie die Scale Methode für ein neues SKCanvas Objekt aufrufen, enthält die resultierende Transformationsmatrix die und sy argumente sx in den diagonalen Zellen:
| sx 0 0 |
| x y 1 | × | 0 sy 0 | = | x' y' z' |
| 0 0 1 |
Die Transformationsformeln sind wie folgt:
x' = sx · x
y' = sy · y
Die Transformationsmatrix nach dem Aufrufen Skew enthält die beiden Argumente in den Matrixzellen neben den Skalierungsfaktoren:
│ 1 ySkew 0 │
| x y 1 | × │ xSkew 1 0 │ = | x' y' z' |
│ 0 0 1 │
Die Transformationsformeln sind:
x' = x + xSkew · y
y' = ySkew · x + y
Für einen Aufruf RotateDegrees oder RotateRadians für einen Winkel von α lautet die Transformationsmatrix wie folgt:
│ cos(α) sin(α) 0 │
| x y 1 | × │ –sin(α) cos(α) 0 │ = | x' y' z' |
│ 0 0 1 │
Hier sind die Transformationsformeln:
x' = cos(α) · x - sin(α) · y
y' = sin(α) · x - cos(α) · y
Wenn α 0 Grad beträgt, handelt es sich um die Identitätsmatrix. Wenn α 180 Grad beträgt, lautet die Transformationsmatrix wie folgt:
| –1 0 0 | | 0 –1 0 | | 0 0 1 |
Eine 180-Grad-Drehung entspricht dem horizontalen und vertikalen Kippen eines Objekts, das auch durch Festlegen von Skalierungsfaktoren von –1 erreicht wird.
Alle diese Arten von Transformationen werden als affine Transformationen klassifiziert. Affine Transformationen beziehen niemals die dritte Spalte der Matrix ein, die bei den Standardwerten 0, 0 und 1 wieder Standard. Im Artikel "Non-Affine Transforms " werden nicht affine Transformationen erläutert.
Matrizenmultiplikation
Ein wesentlicher Vorteil bei der Verwendung der Transformationsmatrix besteht darin, dass zusammengesetzte Transformationen durch Matrixmultiplizierung abgerufen werden können, die häufig in der SkiaSharp-Dokumentation als Verkettung bezeichnet wird. Viele der transformationsbezogenen Methoden SKCanvas beziehen sich auf "Vorverkettung" oder "Vorverkettung". Dies bezieht sich auf die Reihenfolge der Multiplikation, was wichtig ist, da die Matrixmultiplikation nicht kommutativ ist.
Die Dokumentation für die Translate Methode besagt beispielsweise, dass sie die aktuelle Matrix mit der angegebenen Übersetzung vorab verketten soll, während die Dokumentation für die Scale Methode besagt, dass sie die aktuelle Matrix mit der angegebenen Skala verketten.
Dies bedeutet, dass die durch den Methodenaufruf angegebene Transformation der Multiplizierer (der linken Operand) und die aktuelle Transformationsmatrix der Multiplizierer (der rechte Operand) ist.
Angenommen, gefolgt Translate von Scale:
canvas.Translate(tx, ty);
canvas.Scale(sx, sy);
Die Scale Transformation wird durch die Translate Transformation für die zusammengesetzte Transformationsmatrix multipliziert:
| sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | 0 0 1 | | tx ty 1 | | tx ty 1 |
Scale könnte wie Translate folgt aufgerufen werden:
canvas.Scale(sx, sy);
canvas.Translate(tx, ty);
In diesem Fall wird die Reihenfolge der Multiplikation umgekehrt, und die Skalierungsfaktoren werden effektiv auf die Übersetzungsfaktoren angewendet:
| 1 0 0 | | sx 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | = | 0 sy 0 | | tx ty 1 | | 0 0 1 | | tx·sx ty·sy 1 |
Dies ist die Scale Methode mit einem Pivotpunkt:
canvas.Scale(sx, sy, px, py);
Dies entspricht den folgenden Übersetzungs- und Skalierungsaufrufen:
canvas.Translate(px, py);
canvas.Scale(sx, sy);
canvas.Translate(–px, –py);
Die drei Transformationsmatrizen werden in umgekehrter Reihenfolge von der Darstellung der Methoden im Code multipliziert:
| 1 0 0 | | sx 0 0 | | 1 0 0 | | sx 0 0 | | 0 1 0 | × | 0 sy 0 | × | 0 1 0 | = | 0 sy 0 | | –px –py 1 | | 0 0 1 | | px py 1 | | px–px·sx py–py·sy 1 |
Die SKMatrix-Struktur
Die SKMatrix Struktur definiert neun Lese-/Schreibeigenschaften des Typs float , die den neun Zellen der Transformationsmatrix entsprechen:
│ ScaleX SkewY Persp0 │ │ SkewX ScaleY Persp1 │ │ TransX TransY Persp2 │
SKMatrix definiert auch eine Eigenschaft mit dem Namen Values des Typs float[]. Diese Eigenschaft kann verwendet werden, um die neun Werte in einer Aufnahme in der Reihenfolge ScaleX, , SkewXTransX, SkewY, ScaleY, TransY, , Persp0, und Persp1.Persp2
Die Persp0, Persp1und Persp2 Zellen werden im Artikel Non-Affine Transformationen behandelt. Wenn diese Zellen die Standardwerte 0, 0 und 1 aufweisen, wird die Transformation mit einem Koordinatenpunkt wie folgt multipliziert:
│ ScaleX SkewY 0 │
| x y 1 | × │ SkewX ScaleY 0 │ = | x' y' z' |
│ TransX TransY 1 │
x' = ScaleX · x + SkewX · y + TransX
y' = SkewX · x + ScaleY · y + TransY
z' = 1
Dies ist die vollständige zweidimensionale affine Transformation. Die affine Transformation behält parallele Linien bei, was bedeutet, dass ein Rechteck niemals in einen anderen Als ein Parallelogramm umgewandelt wird.
Die SKMatrix Struktur definiert mehrere statische Methoden zum Erstellen von SKMatrix Werten. Diese alle Rückgabewerte SKMatrix :
MakeTranslationMakeScaleMakeScalemit einem PivotpunktMakeRotationfür einen Winkel in BogenmaßMakeRotationfür einen Winkel in Bogenmaßen mit einem PivotpunktMakeRotationDegreesMakeRotationDegreesmit einem PivotpunktMakeSkew
SKMatrix definiert auch mehrere statische Methoden, die zwei Matrizen verketten, was bedeutet, dass sie multipliziert werden. Diese Methoden sind benannt Concat, PostConcatund PreConcates gibt zwei Versionen von jedem. Diese Methoden haben keine Rückgabewerte; Stattdessen verweisen sie über ref Argumente auf vorhandene SKMatrix Werte. Im folgenden Beispiel Asind , , Bund R (für "Result") alle SKMatrix Werte.
Die beiden Concat Methoden werden wie folgt aufgerufen:
SKMatrix.Concat(ref R, A, B);
SKMatrix.Concat(ref R, ref A, ref B);
Die folgenden Multiplikationen werden ausgeführt:
R = B × A
Die anderen Methoden haben nur zwei Parameter. Der erste Parameter wird geändert, und wenn der Methodenaufruf zurückgegeben wird, enthält das Produkt der beiden Matrizen. Die beiden PostConcat Methoden werden wie folgt aufgerufen:
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, ref B);
Diese Aufrufe führen den folgenden Vorgang aus:
A = A × B
Die beiden PreConcat Methoden sind ähnlich:
SKMatrix.PreConcat(ref A, B);
SKMatrix.PreConcat(ref A, ref B);
Diese Aufrufe führen den folgenden Vorgang aus:
A = B × A
Die Versionen dieser Methoden mit allen ref Argumenten sind etwas effizienter beim Aufrufen der zugrunde liegenden Implementierungen, aber es kann verwirrend sein, dass jemand Ihren Code liest und davon ausgeht, dass alles mit einem ref Argument von der Methode geändert wird. Darüber hinaus ist es häufig praktisch, ein Argument zu übergeben, das aus einer der Make Methoden resultiert, z. B.:
SKMatrix result;
SKMatrix.Concat(result, SKMatrix.MakeTranslation(100, 100),
SKMatrix.MakeScale(3, 3));
Dadurch wird die folgende Matrix erstellt:
│ 3 0 0 │ │ 0 3 0 │ │ 100 100 1 │
Dies ist die Skalierungstransformation, die durch die Übersetzungstransformation multipliziert wird. In diesem speziellen Fall stellt die SKMatrix Struktur eine Verknüpfung mit einer Methode mit dem Namen :SetScaleTranslate
SKMatrix R = new SKMatrix();
R.SetScaleTranslate(3, 3, 100, 100);
Dies ist eine der wenigen Male, wenn es sicher ist, den SKMatrix Konstruktor zu verwenden. Die SetScaleTranslate Methode legt alle neun Zellen der Matrix fest. Es ist auch sicher, den SKMatrix Konstruktor mit den statischen Rotate und RotateDegrees Methoden zu verwenden:
SKMatrix R = new SKMatrix();
SKMatrix.Rotate(ref R, radians);
SKMatrix.Rotate(ref R, radians, px, py);
SKMatrix.RotateDegrees(ref R, degrees);
SKMatrix.RotateDegrees(ref R, degrees, px, py);
Diese Methoden verketten keine Drehtransformation mit einer vorhandenen Transformation. Die Methoden legen alle Zellen der Matrix fest. Sie sind funktional identisch mit den MakeRotation Und MakeRotationDegrees Methoden, mit der Ausnahme, dass sie den SKMatrix Wert nicht instanziieren.
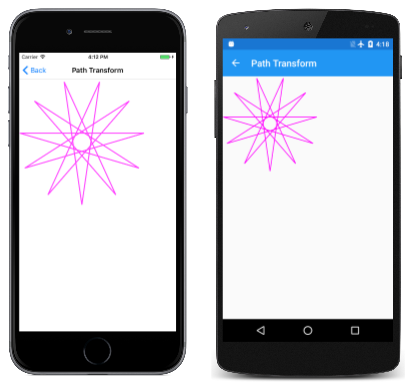
Angenommen, Sie haben ein SKPath Objekt, das Sie anzeigen möchten, aber sie bevorzugen eine etwas andere Ausrichtung oder einen anderen Mittelpunkt. Sie können alle Koordinaten dieses Pfads ändern, indem Sie die Transform Methode mit SKPath einem SKMatrix Argument aufrufen. Auf der Seite "Pfadtransformation " wird die Vorgehensweise veranschaulicht. Die PathTransform Klasse verweist auf das HendecagramPath Objekt in einem Feld, verwendet jedoch seinen Konstruktor, um eine Transformation auf diesen Pfad anzuwenden:
public class PathTransformPage : ContentPage
{
SKPath transformedPath = HendecagramArrayPage.HendecagramPath;
public PathTransformPage()
{
Title = "Path Transform";
SKCanvasView canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
SKMatrix matrix = SKMatrix.MakeScale(3, 3);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeRotationDegrees(360f / 22));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(300, 300));
transformedPath.Transform(matrix);
}
...
}
Das HendecagramPath Objekt hat eine Mitte an (0, 0), und die 11 Punkte des Sterns erstrecken sich von dieser Mitte um 100 Einheiten in alle Richtungen nach außen. Dies bedeutet, dass der Pfad sowohl positive als auch negative Koordinaten aufweist. Die Seite "Pfadtransformation " verwendet lieber dreimal so groß wie ein Stern und alle positiven Koordinaten. Darüber hinaus soll kein Punkt des Sterns gerade nach oben zeigen. Es möchte stattdessen, dass ein Punkt des Sterns gerade nach unten zeigt. (Da der Stern 11 Punkt hat, kann es nicht beides haben.) Dies erfordert eine Drehung des Sterns um 360 Grad dividiert durch 22.
Der Konstruktor erstellt ein SKMatrix Objekt aus drei separaten Transformationen mithilfe der PostConcat Methode mit dem folgenden Muster, wobei A, B und C Instanzen von SKMatrix:
SKMatrix matrix = A;
SKMatrix.PostConcat(ref A, B);
SKMatrix.PostConcat(ref A, C);
Dies ist eine Reihe aufeinander folgender Multiplikationen, sodass das Ergebnis wie folgt lautet:
A × B × C
Die aufeinander folgenden Multiplikationen helfen beim Verständnis der Funktionsweise der einzelnen Transformationen. Die Skalierungstransformation erhöht die Größe der Pfadkoordinaten um den Faktor 3, sodass die Koordinaten zwischen -300 und 300 liegen. Die Drehtransformation dreht den Stern um seinen Ursprung. Die Übersetzungstransformation verschiebt sie dann um 300 Pixel nach rechts und unten, sodass alle Koordinaten positiv werden.
Es gibt andere Sequenzen, die dieselbe Matrix erzeugen. Hier ist eine weitere:
SKMatrix matrix = SKMatrix.MakeRotationDegrees(360f / 22);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeTranslation(100, 100));
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(3, 3));
Dadurch wird der Pfad zuerst um die Mitte gedreht und dann um 100 Pixel nach rechts und unten übersetzt, sodass alle Koordinaten positiv sind. Der Stern wird dann relativ zur neuen linken oberen Ecke vergrößert, was den Punkt (0, 0) darstellt.
Der PaintSurface Handler kann einfach diesen Pfad rendern:
public class PathTransformPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Magenta;
paint.StrokeWidth = 5;
canvas.DrawPath(transformedPath, paint);
}
}
}
Sie wird in der oberen linken Ecke des Zeichenbereichs angezeigt:
Der Konstruktor dieses Programms wendet die Matrix auf den Pfad mit dem folgenden Aufruf an:
transformedPath.Transform(matrix);
Der Pfad behält diese Matrix nicht als Eigenschaft bei. Stattdessen wird die Transformation auf alle Koordinaten des Pfads angewendet. Wenn Transform die Transformation erneut aufgerufen wird, wird die Transformation erneut angewendet, und die einzige Möglichkeit, wie Sie zurückkehren können, besteht darin, eine andere Matrix anzuwenden, die die Transformation rückgängig macht. Glücklicherweise definiert die SKMatrix Struktur eine TryInvert Methode, die die Matrix abruft, die eine bestimmte Matrix umkehrt:
SKMatrix inverse;
bool success = matrix.TryInverse(out inverse);
Die Methode wird aufgerufen TryInverse , da nicht alle Matrizen invertierbar sind, aber eine nicht invertierbare Matrix wird wahrscheinlich nicht für eine Grafiktransformation verwendet.
Sie können eine Matrixtransformation auch auf einen SKPoint Wert, ein Array von Punkten, eine SKRectoder sogar nur eine einzelne Zahl in Ihrem Programm anwenden. Die SKMatrix Struktur unterstützt diese Vorgänge mit einer Sammlung von Methoden, die mit dem Wort Mapbeginnen, z. B. die folgenden:
SKPoint transformedPoint = matrix.MapPoint(point);
SKPoint transformedPoint = matrix.MapPoint(x, y);
SKPoint[] transformedPoints = matrix.MapPoints(pointArray);
float transformedValue = matrix.MapRadius(floatValue);
SKRect transformedRect = matrix.MapRect(rect);
Wenn Sie diese letzte Methode verwenden, denken Sie daran, dass die Struktur nicht in der SKRect Lage ist, ein gedrehtes Rechteck darzustellen. Die Methode ist nur für einen SKMatrix Wert sinnvoll, der Übersetzung und Skalierung darstellt.
Interaktives Experiment
Eine Möglichkeit, ein Gefühl für die affine Transformation zu erhalten, besteht darin, drei Ecken einer Bitmap auf dem Bildschirm interaktiv zu bewegen und zu sehen, welche Transformationsergebnisse erzielt werden. Dies ist die Idee hinter der Seite "Affine Matrix anzeigen". Diese Seite erfordert zwei weitere Klassen, die auch in anderen Demonstrationen verwendet werden:
Die TouchPoint Klasse zeigt einen transluzenten Kreis an, der auf dem Bildschirm gezogen werden kann. TouchPoint erfordert, dass ein SKCanvasView oder ein Element, das ein übergeordnetes Element eines SKCanvasView Elements ist, das TouchEffect angefügt ist. Setzen Sie die Capture-Eigenschaft auf true. TouchAction Im Ereignishandler muss das Programm die ProcessTouchEvent Methode TouchPoint für jede TouchPoint Instanz aufrufen. Die Methode gibt zurück true , wenn das Touchereignis dazu geführt hat, dass sich der Touchpunkt bewegt. Außerdem muss der PaintSurface Handler die Paint Methode in jeder TouchPoint Instanz aufrufen und an das SKCanvas Objekt übergeben.
TouchPoint zeigt eine gängige Methode, wie ein SkiaSharp-Visuelles in einer separaten Klasse gekapselt werden kann. Die Klasse kann Eigenschaften zum Angeben von Merkmalen des visuellen Elements definieren, und eine mit einem SKCanvas Argument benannte Paint Methode kann sie rendern.
Die Center Eigenschaft des TouchPoint Objekts gibt die Position des Objekts an. Diese Eigenschaft kann festgelegt werden, um den Speicherort zu initialisieren. die Eigenschaft ändert sich, wenn der Benutzer den Kreis um den Zeichenbereich zieht.
Die Show Affine Matrix Page erfordert auch die MatrixDisplay Klasse. Diese Klasse zeigt die Zellen eines SKMatrix Objekts an. Es verfügt über zwei öffentliche Methoden: Measure um die Dimensionen der gerenderten Matrix abzurufen und Paint anzuzeigen. Die Klasse enthält eine MatrixPaint Eigenschaft vom Typ SKPaint , die für einen anderen Schriftgrad oder eine andere Farbe ersetzt werden kann.
Die ShowAffineMatrixPage.xaml-Datei instanziiert die SKCanvasView und fügt eine TouchEffectan. Die ShowAffineMatrixPage.xaml.cs CodeBehind-Datei erstellt drei TouchPoint Objekte und legt sie dann auf Positionen fest, die drei Ecken einer Bitmap entsprechen, die sie aus einer eingebetteten Ressource lädt:
public partial class ShowAffineMatrixPage : ContentPage
{
SKMatrix matrix;
SKBitmap bitmap;
SKSize bitmapSize;
TouchPoint[] touchPoints = new TouchPoint[3];
MatrixDisplay matrixDisplay = new MatrixDisplay();
public ShowAffineMatrixPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
touchPoints[0] = new TouchPoint(100, 100); // upper-left corner
touchPoints[1] = new TouchPoint(bitmap.Width + 100, 100); // upper-right corner
touchPoints[2] = new TouchPoint(100, bitmap.Height + 100); // lower-left corner
bitmapSize = new SKSize(bitmap.Width, bitmap.Height);
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
}
...
}
Eine affine Matrix wird durch drei Punkte eindeutig definiert. Die drei TouchPoint Objekte entsprechen den oberen linken, oberen rechten und unteren linken Ecken der Bitmap. Da eine affine Matrix nur in der Lage ist, ein Rechteck in ein Parallelogramm zu transformieren, wird der vierte Punkt von den anderen drei impliziert. Der Konstruktor endet mit einem Aufruf ComputeMatrixvon , der die Zellen eines SKMatrix Objekts aus diesen drei Punkten berechnet.
Der TouchAction Handler ruft die ProcessTouchEvent Methode der einzelnen TouchPoint. Der scale Wert konvertiert von Xamarin.Forms Koordinaten in Pixel:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnTouchEffectAction(object sender, TouchActionEventArgs args)
{
bool touchPointMoved = false;
foreach (TouchPoint touchPoint in touchPoints)
{
float scale = canvasView.CanvasSize.Width / (float)canvasView.Width;
SKPoint point = new SKPoint(scale * (float)args.Location.X,
scale * (float)args.Location.Y);
touchPointMoved |= touchPoint.ProcessTouchEvent(args.Id, args.Type, point);
}
if (touchPointMoved)
{
matrix = ComputeMatrix(bitmapSize, touchPoints[0].Center,
touchPoints[1].Center,
touchPoints[2].Center);
canvasView.InvalidateSurface();
}
}
...
}
Wenn eines TouchPoint verschoben wurde, wird die Methode erneut aufgerufen ComputeMatrix und die Oberfläche ungültig.
Die ComputeMatrix Methode bestimmt die Matrix, die von diesen drei Punkten impliziert wird. Die als "Matrix" bezeichnete A Matrix transformiert ein quadratisches Rechteck mit einem Pixel in ein Parallelogramm basierend auf den drei Punkten, während die aufgerufene S Skalierungstransformation die Bitmap auf ein quadratisches Rechteck mit einem Pixel skaliert. Die zusammengesetzte Matrix ist S × A:
public partial class ShowAffineMatrixPage : ContentPage
{
...
static SKMatrix ComputeMatrix(SKSize size, SKPoint ptUL, SKPoint ptUR, SKPoint ptLL)
{
// Scale transform
SKMatrix S = SKMatrix.MakeScale(1 / size.Width, 1 / size.Height);
// Affine transform
SKMatrix A = new SKMatrix
{
ScaleX = ptUR.X - ptUL.X,
SkewY = ptUR.Y - ptUL.Y,
SkewX = ptLL.X - ptUL.X,
ScaleY = ptLL.Y - ptUL.Y,
TransX = ptUL.X,
TransY = ptUL.Y,
Persp2 = 1
};
SKMatrix result = SKMatrix.MakeIdentity();
SKMatrix.Concat(ref result, A, S);
return result;
}
...
}
Schließlich rendert die PaintSurface Methode die Bitmap basierend auf dieser Matrix, zeigt die Matrix unten auf dem Bildschirm an und rendert die Touchpunkte an den drei Ecken der Bitmap:
public partial class ShowAffineMatrixPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Display the bitmap using the matrix
canvas.Save();
canvas.SetMatrix(matrix);
canvas.DrawBitmap(bitmap, 0, 0);
canvas.Restore();
// Display the matrix in the lower-right corner
SKSize matrixSize = matrixDisplay.Measure(matrix);
matrixDisplay.Paint(canvas, matrix,
new SKPoint(info.Width - matrixSize.Width,
info.Height - matrixSize.Height));
// Display the touchpoints
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
}
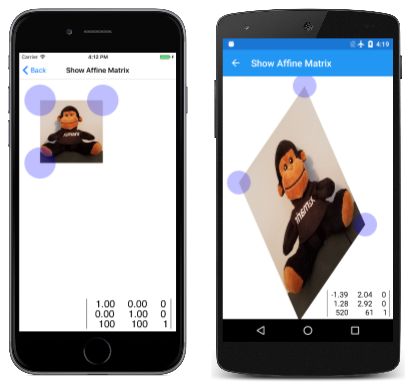
Der folgende iOS-Bildschirm zeigt die Bitmap an, wenn die Seite zum ersten Mal geladen wird, während die beiden anderen Bildschirme nach einer Manipulation angezeigt werden:The iOS screen below shows the bitmap when the page is first loaded, while the two other screen show it after some manipulation:
Obwohl die Fingereingabepunkte die Ecken der Bitmap ziehen, ist dies nur eine Illusion. Die aus den Touchpunkten berechnete Matrix transformiert die Bitmap so, dass die Ecken mit den Berührungspunkten übereinstimmen.
Es ist natürlicher für Benutzer, Bitmaps zu verschieben, zu ändern und zu drehen, die nicht durch Ziehen der Ecken, sondern mit einem oder zwei Fingern direkt auf dem Objekt zum Ziehen, Zusammendrücken und Drehen verwendet werden. Dies wird im nächsten Artikel zur Toucheingabe behandelt.
Der Grund für die 3:3-Matrix
Es kann erwartet werden, dass ein zweidimensionales Grafiksystem nur eine 2:2-Transformationsmatrix erfordert:
│ ScaleX SkewY │
| x y | × │ │ = | x' y' |
│ SkewX ScaleY │
Dies funktioniert für Skalierung, Drehung und sogar Skewing, aber es ist nicht in der Lage, die grundlegendsten Transformationen, die Übersetzung ist.
Das Problem besteht darin, dass die 2:2-Matrix eine lineare Transformation in zwei Dimensionen darstellt. Eine lineare Transformation behält einige grundlegende arithmetische Vorgänge bei, aber eine der Auswirkungen besteht darin, dass eine lineare Transformation niemals den Punkt ändert (0, 0). Eine lineare Transformation macht übersetzung unmöglich.
In drei Dimensionen sieht eine lineare Transformationsmatrix wie folgt aus:
│ ScaleX SkewYX SkewZX │
| x y z | × │ SkewXY ScaleY SkewZY │ = | x' y' z' |
│ SkewXZ SkewYZ ScaleZ │
Die Beschriftung SkewXY der Zelle bedeutet, dass der Wert die X-Koordinate basierend auf den Werten von Y verzerrt. Die Zelle SkewXZ bedeutet, dass der Wert die X-Koordinate basierend auf den Werten von Z verzerrt und Werte für die anderen Skew Zellen ähnlich schief.
Es ist möglich, diese 3D-Transformationsmatrix auf eine zweidimensionale Ebene zu beschränken, indem Sie sie auf "0" und SkewZYScaleZ "1" festlegenSkewZX:
│ ScaleX SkewYX 0 │
| x y z | × │ SkewXY ScaleY 0 │ = | x' y' z' |
│ SkewXZ SkewYZ 1 │
Wenn die zweidimensionalen Grafiken vollständig auf der Ebene im 3D-Raum gezeichnet werden, wobei Z gleich 1 ist, sieht die Transformationsmultiplikation wie folgt aus:
│ ScaleX SkewYX 0 │
| x y 1 | × │ SkewXY ScaleY 0 │ = | x' y' 1 |
│ SkewXZ SkewYZ 1 │
Alles bleibt auf der zweidimensionalen Ebene, wobei Z gleich 1 ist, aber die und SkewYZ die SkewXZ Zellen werden effektiv zu zweidimensionalen Übersetzungsfaktoren.
So dient eine dreidimensionale lineare Transformation als zweidimensionale, nicht lineare Transformation. (Analog dazu basieren Transformationen in 3D-Grafiken auf einer 4:4-Matrix.)
Die SKMatrix Struktur in SkiaSharp definiert Eigenschaften für diese dritte Zeile:
│ ScaleX SkewY Persp0 │
| x y 1 | × │ SkewX ScaleY Persp1 │ = | x' y' z` |
│ TransX TransY Persp2 │
Ungleich Nullwerte von Persp0 und Persp1 führen zu Transformationen, die Objekte aus der zweidimensionalen Ebene verschieben, wobei Z gleich 1 ist. Was passiert, wenn diese Objekte zurück zu dieser Ebene verschoben werden, wird im Artikel zu Non-Affine Transforms behandelt.