Wie kann man die Verschränkung nutzen, um Informationen zu senden?
Die Quantenverschränkung kann eine hervorragende Ressource für die Quantenkommunikation sein. Einer der berühmtesten Anwendungen der Verschränkung ist die Quantenteleportation.
Bei der Teleportation verwenden wir die Verschränkung, um den Zustand eines Qubits von einem Ort zu einem anderen zu übertragen. Der Zustand des Qubits wird auf einen anderen Qubit übertragen, aber der Qubit selbst wird nicht physisch verschoben. Dies ist eine wichtige Sache, die Sie sich merken sollten! Die Informationen über den Status des Qubits werden an einen anderen Qubit übertragen, der als Behälter verwendet wird, um die Informationen des Nachrichtenqubits zu schreiben.
Das Teleportationsprotokoll verwendet eine Kombination aus Verschränkung und klassischer Kommunikation. Die klassische Kommunikation ist wichtig, da das Teleportationsprotokoll den Absender dazu verpflichtet, die Ergebnisse ihrer Messungen an den Empfänger zu kommunizieren. Dies bedeutet, dass wir die Teleportation nicht verwenden können, um Informationen schneller als die Lichtgeschwindigkeit zu senden. Die klassische Kommunikation zwischen dem Absender und dem Empfänger ist durch die Lichtgeschwindigkeit begrenzt.
Sehen wir uns das Protokoll der Quantenteleportation an.
Das Protokoll der Quantenteleportation
Alice und Bob arbeiten in derselben Firma. Alice ist in Seattle ansässig, und Bob ist in Los Angeles ansässig. Sie arbeiten an einem Projekt, für das sie Quanteninformationen freigeben müssen. Sie entscheiden sich, Quantenteleportation zu verwenden, um Quanteninformationen zwischen ihnen zu senden.
Erste Einrichtung
Alice und Bob haben jeweils ein Qubit, das Teil eines zuvor vorbereiteten verschränkten Paares ist. Das verschränkte Paar ist ein Bell-Zustand
$$\ket{\phi}=\frac1{\sqrt2}(\ket{0_A 0_B} + \ket{1_A 1_B})$$
Alice hat ein zusätzliches Qubit – als "Message Qubit" bezeichnet – und möchte diesen Qubit an Bob senden. Der Nachrichten-Qubit den Alice zu Bob teleportieren möchte ist ein unbekannter Zustand. Der Status des Nachrichten Qubits ist
$$\ket{m}=\alpha\ket{{0}_m + \beta\ket{{1}_m,$$
wobei $\alpha$ und $\beta$ komplexe Zahlen sind.
Der globale Zustand von Alice und Bobs drei Qubits ist
$$\ket{\text{Global}}= (\alpha\ket{{0}_m + \beta\ket{1}_m) \otimes\frac1{\sqrt2}(\ket{0_A 0_B}+ \ket{1_A 1_B}) $$
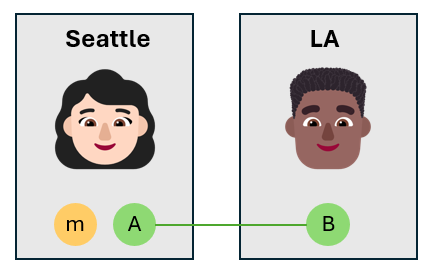
Alice verschränkt den Nachrichten-Qubit mit ihrem eigenen Qubit
Alice nimmt den Nachrichten-Qubit und verschränkt ihn mit ihrem eigenen Qubit $A$ mit einem CNOT-Gate. Der Nachrichten-Qubit ist der Kontroll-Qubit, und Alices Qubit ist der target Qubit. Dadurch wird ein 3-Qubit-verschränkter Zustand erstellt.
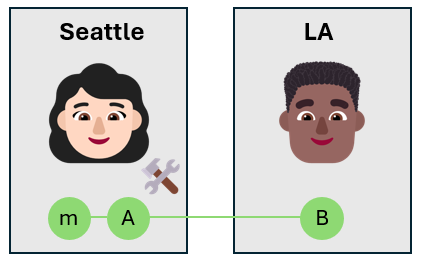
Der Nachrichten-Qubit befindet sich im unbekannten Zustand $\alpha\ket{0}_m + \beta\ket{1}_m$, nach dem Anwenden des CNOT-Gates befinden sich Alices Qubits also in einer Superposition der vier Bell-Zustände. Der globale Zustand der drei Qubits ist
$$\ket{\text{Global}}=\frac1{{2}\ket{\phi^+}_\text{mA} (\alpha\ket{{0}_B + \beta\ket{{1}_B) + $$
$$ + \frac1{{2}\ket{\phi^-}_\text{mA} (\alpha\ket{0}_B - \beta\ket{1}_B) +$$
$$ + \frac1{{2}\ket{\psi^+}_\text{mA}(\alpha\ket{1}_B + \beta\ket{0}_B) + $$
$$ + \frac1{{2}\ket{\psi^-}_\text{mA} (\alpha\ket{1}_B- \beta\ket{0}_B)$$
Der globale Zustand von Alice und Bobs Qubits ist eine Superposition von vier möglichen Zuständen.
Tipp
Eine gute Übung besteht darin, zu überprüfen, ob der globale Zustand der drei Qubits der oben angegebene ist. Sie können dies tun, indem Sie das CNOT-Gate auf das Nachrichten-Qubit und Alices Qubit anwenden und dann den Zustand der drei Qubits erweitern.
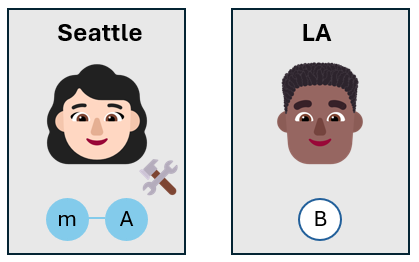
Alice misst die Qubits
Alice misst dann das Nachrichten-Qubit und ihr eigenes Qubit. Sie misst die Qubits in der $Z-Basis$nicht wie gewohnt, aber sie wählt die Bell-Basis aus. Die Bell-Basis besteht aus den vier Bell-Zuständen $\lbrace \ket{\phi^+}, \ket{\phi^-}, \ket{\psi^+}, \ket{\psi^-} \rbrace$.
Durch die Messung des Nachrichten-Qubits und ihres eigenen Qubits auf der Bell-Basis projiziert Alice ihre Qubits in einen der vier Bell-Zustände. Da die drei Qubits verschränkt sind, werden die Messergebnisse korreliert. Wenn Alice ihre Qubits misst, wird Bobs Qubit auch in den korrelierten Zustand projiziert.
Wenn Alice beispielsweise ihre Qubits misst und den Zustand $\ket{\phi^-}$ beobachtet, wird Bobs Qubit in den Zustand $\alpha\ket{0}_B - \beta\ket{1}_B$ projiziert.
Andrea ruft Bob an
Alice ruft Bob an und teilt ihm die Ergebnisse ihrer Messungen mit. Sie verwendet einen klassischen Kommunikationskanal, z. B. einen Telefonanruf oder eine Sms.
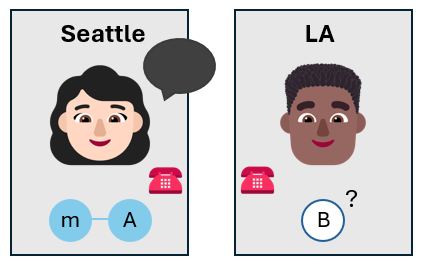
Bob kennt nun den Zustand seines eigenen Qubits, ohne ihn messen zu müssen. Der Zustand von Bobs Qubit ist möglicherweise nicht derselbe wie der Zustand des Nachrichten-Qubits, das Alice teleportieren wollte, aber er kommt diesem nahe.
Bob wendet einen Quantenvorgang an
Als Nächstes kann Bob den ursprünglichen Zustand des Nachrichten-Qubits wiederherstellen, indem er einen bestimmten Quantenvorgang auf seinen Qubit anwendet. Der Vorgang, den Bob durchführt, hängt davon ab, was Alice ihm am Telefon gesagt hat.
Der von ihm ausgeführte Vorgang kann ein Pauli $X-Gate$, ein Pauli $Z-Gate$, beides oder keines sein.
Wenn beispielsweise das Ergebnis der Messung von Alice $\ket{\phi^-}$ ist, weiß Bob, dass sein Qubit den Zustand $(\alpha\ket{0}_B - \beta\ket{1}_B)$ hat. Er muss nur ein Pauli Z-Gate anwenden, um den ursprünglichen Zustand des Nachrichten-Qubits wiederherzustellen.
| Alice misst | Bob wendet |
|---|---|
| $\ket{\phi^+}$ | Keine Operation |
| $\ket{\phi^-}$ | Pauli Z-Gate |
| $\ket{\psi^+}$ | Pauli X-Gate |
| $\ket{\psi^-}$ | Pauli X-Gate gefolgt von Pauli Z-Gate |
Dieser letzte Vorgang teleportiert effektiv den Status des Nachrichten-Qubits auf Bobs Qubit. Mission erfüllt!
Wichtig
Das Anwenden eines Vorgangs auf ein Qubit ist nicht mit der Messung identisch. Wenn Bob den Vorgang anwendet, misst er seinen Qubit nicht. Er wendet einen Quantenvorgang an, der den Zustand des Qubits ändert, aber ihn nicht reduziert.