Binäre Klassifizierung
Klassifizierung ist wie Regression eine beaufsichtigte maschinelle Lerntechnik und folgt daher demselben iterativen Prozess des Trainings, der Validierung und der Evaluierung von Modellen. Anstatt wie bei einem Regressionsmodell numerische Werte zu berechnen, berechnen die zum Trainieren von Klassifizierungsmodellen verwendeten AlgorithmenWahrscheinlichkeitswerte Wahrscheinlichkeitswerte für die Klassenzuordnung, und die zur Bewertung der Modellleistung verwendeten Auswertungsmetriken vergleichen die vorhergesagten Klassen mit den tatsächlichen Klassen.
Binäre Klassifizierungsalgorithmen werden verwendet, um ein Modell zu trainieren, das eine von zwei möglichen Bezeichnungen für eine einzelne Klasse vorhersagt. Im Wesentlichen dienen sie zur Vorhersage von true bzw. wahr oder false bzw falsch. In den meisten realen Szenarien bestehen die Datenbeobachtungen, die zum Trainieren und Überprüfen des Modells verwendet werden, aus mehreren Featurewerten (x) und einem y-Wert, der entweder 1 oder 0 lautet.
Beispiel für binäre Klassifizierung
Um zu verstehen, wie die binäre Klassifizierung funktioniert, sehen wir uns ein vereinfachtes Beispiel an, in dem anhand eines einzelnen Features (x) vorhergesagt wird, ob die Bezeichnung y 1 oder 0 ist. In diesem Beispiel verwenden wir den Blutzuckerspiegel von Patient*innen, um vorherzusagen, ob die Patient*innen an Diabetes leiden oder nicht. Hier sind die Daten, mit denen wir das Modell trainieren:
 |
 |
|---|---|
| Blutzucker (x) | Diabetiker? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Trainieren eines binären Klassifizierungsmodells
Zum Trainieren des Modells verwenden wir einen Algorithmus, um die Trainingsdaten an eine Funktion anzupassen, die die Wahrscheinlichkeit berechnet, dass die Klassenbezeichnung wahr ist (mit anderen Worten, dass die Person Diabetes hat). Die Wahrscheinlichkeit wird als Wert zwischen 0,0 und 1,0 gemessen, wobei die Gesamtwahrscheinlichkeit für alle möglichen Klassen 1,0 beträgt. Wenn z. B. die Wahrscheinlichkeit, dass ein Patient Diabetiker ist, 0,7 beträgt, dann liegt die Wahrscheinlichkeit, dass er kein Diabetiker ist, entsprechend bei 0,3.
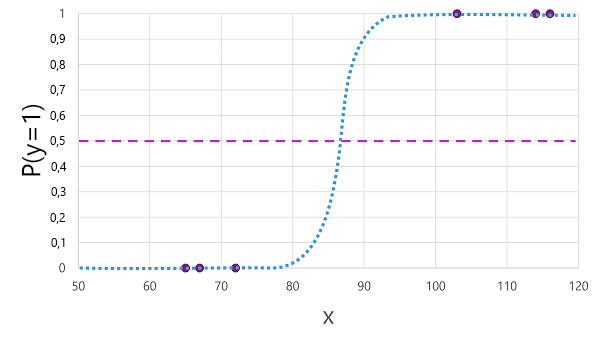
Es gibt viele Algorithmen, die für die binäre Klassifizierung verwendet werden können, z. B . die logistische Regression, die wie folgt eine Sigmoidfunktion (S-förmige Funktion) mit Werten zwischen 0,0 und 1,0 ableitet:
Hinweis
Trotz des Namens wird die logistische Regressionbeim maschinellen Lernen für die Klassifizierung und nicht für die Regression verwendet. Wichtig ist die logistische Natur der von ihr erzeugten Funktion, die eine S-förmige Kurve zwischen einem unteren und oberen Wert (0,0 und 1,0 bei Verwendung für die binäre Klassifizierung) beschreibt.
Die vom Algorithmus erzeugte Funktion beschreibt die Wahrscheinlichkeit, dassy für einen bestimmten Wert von x wahr ist (y=1). Mathematisch lässt sich die Funktion wie folgt ausdrücken:
f(x) = P(y=1 | x)
Bei drei der sechs Beobachtungen in den Trainingsdaten wissen wir, dass y definitiv wahr ist. Für diese Beobachtungen beträgt die Wahrscheinlichkeit, dass y=1 ist, daher 1,0, und bei den anderen drei Beobachtungen wissen wir, dass y definitiv falsch ist, sodass die Wahrscheinlichkeit, dass y=1 ist, hier 0,0 beträgt. Die S-förmige Kurve beschreibt die Wahrscheinlichkeitsverteilung, sodass das Aufragens eines Werts von x auf der Linie die entsprechende Wahrscheinlichkeit angibt, dass y gleich 1 ist.
Das Diagramm enthält auch eine horizontale Linie, um den Schwellenwert anzugeben, ab dem ein Modell basierend auf dieser Funktion true (1) oder false (0) vorhersagt. Der Schwellenwert liegt in der Mitte für y (P(y) = 0,5). Für alle Werte, die an diesem Punkt oder darüber liegen, sagt das Modell true (1) vorher, während es für alle Werte unterhalb dieses Punkts false (0) vorhersagt. Für eine Person mit einem Blutzuckerspiegel von 90 würde die Funktion beispielsweise einen Wahrscheinlichkeitswert von 0,9 ergeben. Da 0,9 höher als der Schwellenwert von 0,5 ist, würde das Modell true vorhersagen (1) – mit anderen Worten, es würde vorhergesagt, dass die Person Diabetes hat.
Auswerten eines binären Klassifizierungsmodells
Wie bei der Regression halten Sie beim Training eines binären Klassifikationsmodells eine zufällige Teilmenge der Daten zurück, mit der Sie das trainierte Modell validieren. Angenommen, wir haben die folgenden Daten zur Validierung unseres Diabetesklassifizierers zurückgehalten:
| Blutzucker (x) | Diabetiker? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
Wenn wir die zuvor abgeleitete logistische Funktion auf die x-Werte anwenden, ergibt sich das folgende Diagramm.
Je nachdem, ob die von der Funktion berechnete Wahrscheinlichkeit über oder unter dem Schwellenwert liegt, generiert das Modell für jede Beobachtung eine vorhergesagte Bezeichnung von 1 oder 0. Anschließend können wir die vorhergesagten Klassenbezeichnungen (ŷ) mit den tatsächlichen Klassenbezeichnungen (y) vergleichen, wie hier gezeigt:
| Blutzucker (x) | Tatsächliche Diabetesdiagnose (y) | Vorhergesagte Diabetesdiagnose (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Auswertungsmetriken der binären Klassifizierung
Der erste Schritt bei der Berechnung von Auswertungsmetriken für ein binäres Klassifizierungsmodell besteht in der Regel darin, eine Matrix mit der Anzahl der richtigen und falschen Vorhersagen für jede mögliche Klassenbezeichnung zu erstellen:
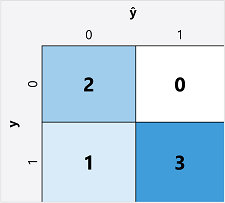
Diese Visualisierung wird als Konfusionsmatrix bezeichnet und zeigt die Vorhersagesummen an, wobei Folgendes gilt:
- ŷ=0 und y=0: True Negatives (TN)
- ŷ=1 und y=0: Falsch positiv (FP)
- ŷ=0 und y=1: Falsch negativ (FN)
- ŷ=1 und y=1: True Positives (TP)
Die Konfusionsmatrix ist so angeordnet, dass richtige (true) Vorhersagen in einer diagonalen Linie von oben links nach rechts unten angezeigt werden. Häufig wird die Farbintensität verwendet, um die Anzahl der Vorhersagen in jeder Zelle anzuzeigen, sodass ein kurzer Blick auf ein Modell, das gute Vorhersagen macht, einen stark schattierten diagonalen Trend erkennen lässt.
Genauigkeit
Die einfachste Metrik, die Sie aus der Konfusionsmatrix berechnen können, ist die Genauigkeit: der Anteil der richtigen Vorhersagen des Modells. Die Genauigkeit wird folgendermaßen berechnet:
(TN+TP) ÷ (TN+FN+FP+TP)
Im Fall unseres Diabetesbeispiels lautet die Berechnung:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0,83
Für unsere Validierungsdaten lieferte das Diabetesklassifizierungsmodell also in 83 % der Fälle korrekte Vorhersagen.
Genauigkeit mag zunächst wie eine gute Metrik zum Auswerten eines Modells erscheinen, doch berücksichtigen Sie Folgendes. Angenommen, 11 % der Bevölkerung hat Diabetes. Sie könnten ein Modell erstellen, das immer 0 vorhersagt, und es würde eine Genauigkeit von 89 % erreichen, obwohl es keinen wirklichen Versuch unternimmt, zwischen Patient*innen zu unterscheiden, indem es ihre Features bewertet. Was wir wirklich benötigen, ist ein tieferes Verständnis dafür, wie das Modell bei der Vorhersage von 1 für positive Fälle und 0 für negative Fälle abschneidet.
Rückruf
Abruf ist eine Metrik, die den Anteil positiver Fälle misst, die das Modell richtig identifiziert hat. Mit anderen Worten, bei wie vielen Personen im Vergleich zur Anzahl der Personen mit Diabetes hat das Modell Diabetes vorhergesagt?
Die Formel für den Abruf lautet:
TP ÷ (TP+FN)
Für unser Diabetesbeispiel gilt:
3 ÷ (3+1)
= 3 ÷ 4
= 0,75
Unser Modell hat also 75 % der Patient*inen mit Diabetes richtig als Diabetiker*innen identifiziert.
Precision
Genauigkeit ist eine ähnliche Metrik wie der Abruf, misst jedoch den Anteil der vorhergesagten positiven Fälle, in denen die wahre Bezeichnung tatsächlich positiv ist. Mit anderen Worten: Welcher Anteil der Patient*innen, für die das Modell vorhergesagt hat, hat tatsächlich Diabetes?
Die Formel für Genauigkeit lautet:
TP ÷ (TP+FP)
Für unser Diabetesbeispiel gilt:
3 ÷ (3+0)
= 3 ÷ 3
= 1,0
Also haben 100 % der Patient*innen, für die unser Modell Diabetes vorhersagt, haben tatsächlich Diabetes.
F1-Score
F1-Score ist eine Gesamtmetrik, die Abruf und Genauigkeit kombiniert. Die Formel für F1-Score lautet wie folgt:
(2 x Genauigkeit x Abruf) ÷ (Genauigkeit + Abruf)
Für unser Diabetesbeispiel gilt:
(2 x 1,0 x 0,75) ÷ (1,0 + 0,75)
= 1,5 ÷ 1,75
= 0,86
AUC (Area under the curve, Fläche unter der Kurve)
Ein anderer Name für den Abruf ist die True Positive Rate (TPR), und es gibt eine äquivalente Metrik namens False Positive Rate (FPR), die mit FP÷(FP+TN) berechnet wird. Wir wissen bereits, dass der TPR-Wert für unser Modell bei Verwendung eines Schwellenwerts von 0,5 gleich 0,75 ist, und wir können die Formel für FPR verwenden, um einen Wert von 0÷2 = 0 zu berechnen.
Wenn wir den Schwellenwert ändern würden, über dem das Modell true (1) vorhersagt, würde dies natürlich die Anzahl der positiven und negativen Vorhersagen beeinflussen und daher die TPR- und FPR-Metriken ändern. Diese Metriken werden häufig verwendet, um ein Modell auszuwerten, indem eine ROC-Kurve (Received Operator Characteristic) dargestellt wird, die TPR und FPR für jeden möglichen Schwellenwert zwischen 0,0 und 1,0 vergleicht:
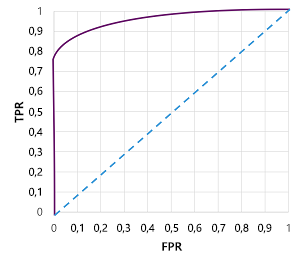
Die ROC-Kurve für ein perfektes Modell würde an der TPR-Achse links gerade nach oben und dann über die FPR-Achse oben verlaufen. Da der Plotbereich für die Kurve 1x1 misst, wäre der Bereich unter dieser perfekten Kurve 1,0 (was bedeutet, dass das Modell in 100 % der Fälle richtig ist). Eine diagonale Linie von links unten nach rechts oben stellt dagegen die Ergebnisse dar, die durch das zufällige Erraten einer binären Bezeichnung erzielt würden. Dies ergibt eine Fläche unter der Kurve von 0,5. Mit anderen Worten: Bei zwei möglichen Klassenbezeichnungen ist vernünftigerweise davon auszugehen, dass diese in 50 % der Fälle korrekt erraten werden.
Im Fall unseres Diabetesmodells wird die obige Kurve erzeugt, und die Metrik der Fläche unter der Kurve (AUC, Area under the curve) beträgt 0,875. Da der AUC-Wert über 0,5 liegt, können wir daraus schließen, dass das Modell besser vorhersagen kann, ob Patient*innen Diabetes haben oder nicht, als wenn es zufällig geraten würde.