Multiklassen-Klassifizierung

Abgeschlossen

Die Multiklassenklassifizierung wird verwendet, um vorherzusagen, zu welcher von mehreren möglichen Klassen eine Beobachtung gehört. Als überwachte Machine Learning-Technik folgt sie demselben iterativen Trainings-, Überprüfungs- und Auswertungsprozess wie die Regression und binäre Klassifizierung, bei denen eine Teilmenge der Trainingsdaten zurückgehalten wird, um das trainierte Modell zu überprüfen.

Beispiel: Multiklassen-Klassifizierung

Algorithmen zur Multiklassen-Klassifizierung werden verwendet, um Wahrscheinlichkeitswerte für mehrere Klassenbezeichnungen zu berechnen, sodass ein Modell die wahrscheinlichste Klasse für eine bestimmte Beobachtung vorhersagen kann.

Sehen wir uns ein Beispiel an, in dem wir einige Beobachtungen von Pinguinen haben, in denen die Flipperlänge (x) jedes Pinguins aufgezeichnet wird. Für jede Beobachtung enthalten die Daten die Pinguinart (y), die wie folgt codiert ist:

• 0: Adeliepinguin
• 1: Eselspinguin
• 2: Zügelpinguin

Hinweis

Wie bei den vorherigen Beispielen in diesem Modul würde ein reales Szenario mehrere Featurewerte (x) enthalten. Wir verwenden der Einfachheit halber ein einzelnes Feature.

Flipperlänge (x)	Art (y)
167	0
172	0
225	2
197	1
189	1
232	2
158	0

Training eines Multiklassen-Klassifizierungsmodells

Zum Trainieren eines Multiklassen-Klassifizierungsmodells müssen wir einen Algorithmus verwenden, um die Trainingsdaten an eine Funktion anzupassen, die einen Wahrscheinlichkeitswert für jede mögliche Klasse berechnet. Es gibt zwei Arten von Algorithmus, die Sie dazu verwenden können:

• One-vs-Rest-Algorithmen (OvR)
• Multinomiale Algorithmen

One-vs-Rest-Algorithmen (OvR)

One-vs-Rest-Algorithmen trainieren eine binäre Klassifizierungsfunktion für jede Klasse, wobei jeweils die Wahrscheinlichkeit berechnet wird, dass die Beobachtung ein Beispiel für die Zielklasse ist. Jede Funktion berechnet die Wahrscheinlichkeit, dass die Beobachtung eine bestimmte Klasse im Vergleich zu jeder anderen Klasse ist. Für unser Klassifizierungsmodell für Pinguinarten würde der Algorithmus im Wesentlichen drei binäre Klassifizierungsfunktionen erstellen:

• f⁰(x) = P(y=0 | x)
• f¹(x) = P(y=1 | x)
• f²(x) = P(y=2 | x)

Jeder Algorithmus erzeugt eine Sigmoidfunktion, die einen Wahrscheinlichkeitswert zwischen 0,0 und 1,0 berechnet. Ein Modell, das mit dieser Art von Algorithmus trainiert wurde, sagt die Klasse für die Funktion voraus, die die höchste Wahrscheinlichkeitsausgabe erzeugt.

Multinomiale Algorithmen

Alternativ können Sie einen multinomialen Algorithmus verwenden, der eine einzelne Funktion erstellt, die eine mehrwertige Ausgabe zurückgibt. Die Ausgabe ist ein Vektor (ein Array von Werten), der die Wahrscheinlichkeitsverteilung für alle möglichen Klassen enthält – mit einem Wahrscheinlichkeitsscore für jede Klasse, für die Folgendes gilt, wenn ihre Summe 1,0 ergibt:

f(x) =[P(y=0|x), P(y=1|x), P(y=2|x)]

Ein Beispiel für diese Art von Funktion ist eine softmax-Funktion, die eine Ausgabe wie im folgenden Beispiel erzeugen könnte:

[0,2; 0,3; 0,5]

Die Elemente im Vektor stellen die Wahrscheinlichkeiten für die Klassen 0, 1 bzw. 2 dar; In diesem Fall ist die Klasse mit der höchsten Wahrscheinlichkeit also 2.

Unabhängig davon, welcher Algorithmustyp verwendet wird, verwendet das Modell die resultierende Funktion, um die wahrscheinlichste Klasse für bestimmte Merkmale (x) zu bestimmen und die entsprechende Klassenbezeichnung (y) vorherzusagen.

Auswerten eines Multiklassen-Klassifizierungsmodells

Sie können einen Multiklassen-Klassifizierer auswerten, indem Sie binäre Klassifizierungsmetriken für jede einzelne Klasse berechnen. Alternativ können Sie Aggregatmetriken berechnen, die alle Klassen berücksichtigen.

Angenommen, wir haben unseren Multiklassen-Klassifizierer überprüft und die folgenden Ergebnisse erhalten:

Flipperlänge (x)	Tatsächliche Art (y)	Vorhergesagte Art (ŷ)
165	0	0
171	0	0
205	2	1
195	1	1
183	1	1
221	2	2
214	2	2

Die Konfusionsmatrix für einen Klassifizierer mit mehreren Klassen ähnelt der eines binären Klassifizierers, mit der Ausnahme, dass sie die Anzahl der Vorhersagen für jede Kombination von vorhergesagten (ŷ) und tatsächlichen Klassenbezeichnungen (y) anzeigt:

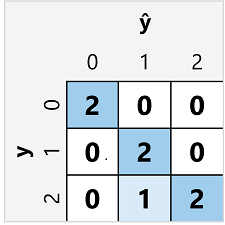
Anhand dieser Konfusionsmatrix können wir die Metriken für jede einzelne Klasse wie folgt bestimmen:

Klasse	TP	TN	FP	FN	Genauigkeit	Recall	Precision	F1-Bewertung
0	2	5	0	0	1.0	1.0	1.0	1.0
1	2	4	1	0	0.86	1.0	0,67	0.8
2	2	4	0	1	0.86	0,67	1.0	0.8

Zum Berechnen der allgemeinen Genauigkeits-, Abruf- und Genauigkeitsmetriken verwenden Sie die Summe der TP-, TN-, FP- und FN-Metriken:

• Gesamtgenauigkeit = (13+6)÷(13+6+1+1) = 0,90
• Gesamtabruf = 6÷(6+1) = 0,86
• Gesamtgenauigkeit = 6÷(6+1) = 0,86

Die F1-Gesamtbewertung wird unter Verwendung der Gesamtrückruf- und Gesamtgenauigkeitsmetriken berechnet:

• Gesamtbewertung F1 = (2×0,86×0,86)÷(0,86+0,86) = 0,86