Deep Learning

Abgeschlossen

Deep Learning ist eine weiterentwickelte Form von maschinellem Lernen, die zu emulieren versucht, wie das menschliche Gehirn lernt. Der Schlüssel zu Deep Learning ist die Bildung eines künstlichen neuronalen Netzes, das die elektrochemische Aktivität in biologischen Neuronen mithilfe mathematischer Funktionen simuliert, wie hier gezeigt.

Biologisches neuronales Netz	Künstliches neuronales Netz
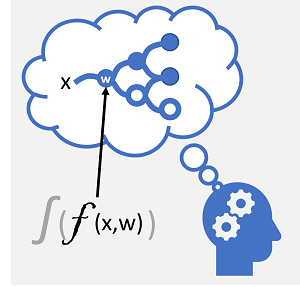
Neuronen werden als Reaktion auf elektrochemische Reize ausgelöst. Das ausgelöste Signal wird an verbundene Neuronen übergeben.	Jedes Neuron ist eine Funktion, die mit einem Eingabewert (x) und einer Gewichtung (w) im Zusammenhang steht. Die Funktion ist in eine Aktivierungsfunktion eingeschlossen, die bestimmt, ob die Ausgabe übergeben werden soll.

Künstliche neuronale Netze bestehen aus mehreren Neuronenschichten, die im Wesentlichen eine tief geschachtelte Funktion definieren. Diese Architektur ist der Grund, warum die Technik als Deep Learning bezeichnet wird, und die von ihr erstellten Modelle werden oft als tiefe neuronale Netze (Deep Neural Networks, DNNs) bezeichnet. Sie können tiefe neuronale Netze für viele Arten von Problemen beim maschinellen Lernen verwenden, einschließlich Regression und Klassifizierung, sowie für speziellere Modelle für die linguistische Datenverarbeitung und das maschinelle Sehen.

Genau wie andere Techniken für das maschinelle Lernen, die in diesem Modul erläutert werden, umfasst Deep Learning das Anpassen von Trainingsdaten an eine Funktion, die eine Bezeichnung (y) basierend auf dem Wert eines oder mehrerer Features (x) vorhersagen kann. Die Funktion (f(x)) ist die äußere Schicht einer geschachtelten Funktion, in der jede Schicht des neuronalen Netzes Funktionen kapselt, die mit x und den zugeordneten Werten für die Gewichtung (w) in Zusammenhang stehen. Der zum Trainieren des Modells verwendete Algorithmus umfasst die iterative Weiterleitung der Featurewerte (x) in den Trainingsdaten durch die Schichten, um Ausgabewerte für ŷ zu berechnen. Dabei wird das Modell überprüft, um zu ermitteln, wie weit die berechneten ŷ-Werte von den bekannten y-Werten abweichen (so wird die Fehlermenge oder der Verlust im Modell quantifiziert). Anschließend werden die Gewichtungen (w) geändert, um den Verlust zu reduzieren. Das trainierte Modell enthält die endgültigen Gewichtungswerte, die zu den genauesten Vorhersagen führen.

Beispiel – Verwenden von Deep Learning für die Klassifizierung

Um besser zu verstehen, wie ein Deep Neural Network-Modell funktioniert, sehen wir uns ein Beispiel an, in dem ein neuronales Netz verwendet wird, um ein Klassifizierungsmodell für Pinguinarten zu definieren.

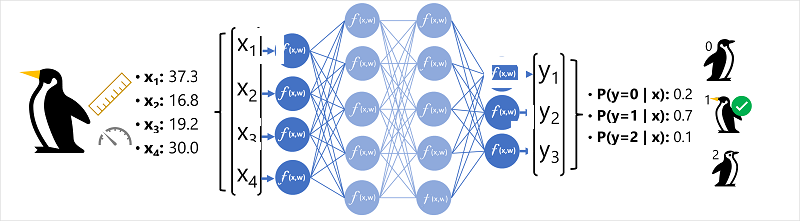
Die Featuredaten (x) bestehen aus einigen Abmessungen der Körperteile eines Pinguins. Dabei handelt es sich um die folgenden Maße:

• Die Schnabellänge des Pinguins
• Die Schnabeltiefe des Pinguins
• Die Länge der Flossen des Pinguins.
• Das Gewicht des Pinguins

In diesem Fall ist x ein Vektor aus vier Werten, der mathematisch als x=[x1,x2,x3,x4] ausgedrückt wird.

Die vorherzusagende Bezeichnung (y) ist die Art des Pinguins. Drei Arten sind möglich:

• Adeliepinguin
• Eselspinguin
• Zügelpinguin

Dies ist ein Beispiel für ein Klassifizierungsproblem, bei dem das Machine Learning-Modell die Klasse vorhersagen muss, zu der eine Beobachtung am wahrscheinlichsten gehört. Ein Klassifizierungsmodell erreicht dies durch Vorhersagen eines Labels, das aus der Wahrscheinlichkeit für jede Klasse besteht. Anders ausgedrückt: y ist ein Vektor mit drei Wahrscheinlichkeitswerten, je einem für die drei möglichen Klassen: [P(y=0|x), P(y=1|x), P(y=2|x)].

Zum Ableiten einer vorhergesagten Pinguinart (Klasse) mit diesem Netz wird der folgende Prozess verwendet:

1. Der Featurevektor für eine Pinguinbeobachtung wird in die Eingabeschicht des neuronalen Netzes eingespeist, die aus einem Neuron für jeden x-Wert besteht. In diesem Beispiel wird der folgende x-Vektor als Eingabe verwendet: [37,3, 16,8, 19,2, 30,0]
2. Die Funktionen für die erste Neuronenschicht berechnen jeweils eine gewichtete Summe, indem sie den x-Wert und die w-Gewichtung kombinieren. Sie übergeben die Summe dann an eine Aktivierungsfunktion, die bestimmt, ob die Summe den Schwellenwert für die Übergabe an die nächste Schicht erreicht.
3. Jedes Neuron in einer Schicht ist mit allen Neuronen der nächsten Schicht verbunden (diese Architektur wird manchmal als vollständig verbundenes Netzwerk bezeichnet). Deshalb werden die Ergebnisse jeder Schicht durch das Netzwerk weitergeleitet, bis sie die Ausgabeschicht erreichen.
4. Die Ausgabeschicht erzeugt einen Vektor von Werten. In diesem Fall wird eine softmax- oder eine ähnliche Funktion verwendet, um die Wahrscheinlichkeitsverteilung für die drei möglichen Klassen von Pinguinen zu berechnen. In diesem Beispiel lautet der Ausgabevektor: [0,2, 0,7, 0,1]
5. Die Elemente des Vektors stellen die Wahrscheinlichkeiten für die Klassen 0, 1 und 2 dar. Der zweite Wert ist der höchste. Deshalb sagt das Modell vorher, dass die Art des Pinguins 1 (Eselspinguin) ist.

Wie lernt ein neuronales Netz?

Die Gewichtungen in einem neuronalen Netz beeinflussen maßgeblich, wie die vorhergesagten Werte für Bezeichnungen berechnet werden. Während des Trainingsprozesses lernt das Modell die Gewichtungen, die zu den genauesten Vorhersagen führen. Wir werden den Trainingsprozess etwas ausführlicher untersuchen, um zu verstehen, wie dieses Lernen stattfindet.

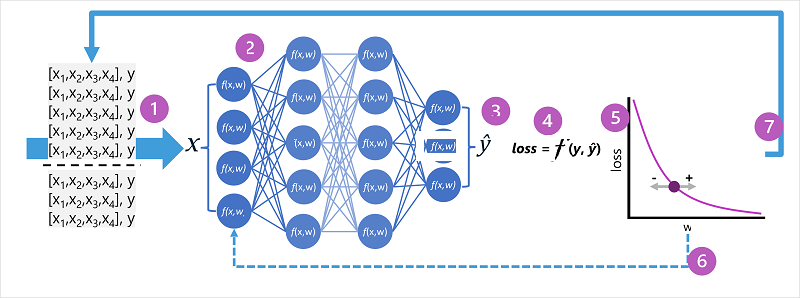
1. Die Datasets für Training und Validierung werden definiert, und die Trainingsfeatures werden in die Eingabeschicht eingespeist.
2. Die Neuronen in jeder Schicht des Netzes wenden ihre Gewichtungen an (die zunächst zufällig zugewiesen werden) und übertragen die Daten über das Netz.
3. Die Ausgabeschicht erzeugt einen Vektor, der die berechneten Werte für ŷ enthält. Die Ausgabe für die Vorhersage einer Pinguinart (Klasse) kann beispielsweise folgendermaßen lauten: [0,3. 0,1. 0,6].
4. Eine Verlustfunktion wird verwendet, um die vorhergesagten ŷ-Werte mit den bekannten y-Werten zu vergleichen und die Differenz (die als Verlust bezeichnet wird) zu aggregieren. Angenommen, die bekannte Klasse für den Fall, der die Ausgabe im vorherigen Schritt zurückgegeben hat, ist Zügelpinguin. In diesem Fall sollte der y-Wert [0,0, 0,0, 1,0] lauten. Die absolute Differenz zwischen diesem Wert und dem ŷ-Vektor ist [0,3, 0,1, 0,4]. In Wirklichkeit berechnet die Verlustfunktion die aggregierte Abweichung für mehrere Fälle und summiert sie zu einem einzelnen Verlustwert.
5. Da das gesamte Netz im Wesentlichen eine große geschachtelte Funktion ist, kann eine Optimierungsfunktion über eine Differenzialrechnung bestimmen, welchen Einfluss die einzelnen Gewichtungen im Netz auf den Verlust haben. Dann kann bestimmt werden, wie die Gewichtungen nach oben oder unten angepasst werden können, um den Gesamtverlust zu reduzieren. Die spezifische Optimierungsmethode kann variieren, umfasst jedoch in der Regel einen Gradientenabstieg, bei dem jede Gewichtung erhöht oder verringert wird, um den Verlust zu minimieren.
6. Die Änderungen an den Gewichtungen werden auf die Schichten im Netz neu angewendet, wodurch die zuvor verwendeten Werte ersetzt werden.
7. Der Prozess wird über mehrere Iterationen (als Epochen bezeichnet) wiederholt, bis der Verlust minimiert ist und das Modell eine Vorhersage mit akzeptabler Genauigkeit liefert.

Hinweis

Es ist zwar einfacher, sich den Vorgang so vorzustellen, dass jeder Fall in den Trainingsdaten nacheinander durch das Netz geleitet wird. Tatsächlich werden die Daten aber in Matrizen zusammengefasst und mithilfe von linearen algebraischen Berechnungen verarbeitet. Deshalb werden neuronale Netze am besten auf Computern mit GPUs trainiert, die für die Vektor- und Matrixbearbeitung optimiert sind.