Analysieren der Klassifizierung mit Grenzwertoptimierungskurven

  • 4 Minuten

Klassifizierungsmodelle müssen einer Kategorie eine Stichprobe zuweisen. Beispielsweise müssen Features wie Größe, Farbe und Bewegung verwendet werden, um zu bestimmen, ob ein Objekt ein Wanderer oder ein Baum ist.

Klassifizierungsmodelle können auf viele Weisen verbessert werden. Beispielsweise können Sie dafür sorgen, dass Ihre Daten ausgeglichen, bereinigt und skaliert sind. Sie können auch die Modellarchitektur ändern und Hyperparameter verwenden, um so viel Leistung wie möglich aus den Daten und der Architektur herauszuholen. Irgendwann stellen Sie dann fest, dass die Leistung des Testdatensatzes (oder Hold-out-Datensatzes) nicht mehr verbessert werden kann und erklären Ihr Modell für bereit.

Bis zu diesem Punkt kann die Modelloptimierung komplex sein. Es gibt jedoch einen einfachen letzten Schritt, um die Funktionsweise des Modells weiter zu verbessern. Für ein besseres Verständnis müssen zunächst ein paar Grundlagen wiederholt werden.

Wahrscheinlichkeiten und Kategorien

Viele Modelle verfügen über mehrere Entscheidungsphasen, und die letzte Phase ist häufig einfach ein Binarisierungsschritt. Während der Binarisierung werden Wahrscheinlichkeiten in eine harte Bezeichnung konvertiert. Nehmen Sie beispielsweise an, dass dem Modell Features bereitgestellt werden und berechnet wird, dass mit einer Wahrscheinlichkeit von 75 % Wandernde gezeigt wurden und mit einer Wahrscheinlichkeit von 25 % Bäume. Ein Objekt kann nicht zu 75 % Wandernde*r und zu 25 % Baum sein – nur eine der beiden Möglichkeiten kann zutreffen. Daher wendet das Modell einen Schwellenwert an, der normalerweise 50 % beträgt. Da die hiker-Klasse größer als 50 % ist, wird das Objekt als Wanderer deklariert.

Der Schwellenwert von 50 % ist eine logische Wahl, denn er bedeutet, dass immer die laut dem Modell wahrscheinlichste Bezeichnung ausgewählt wird. Wenn das Modell jedoch unausgewogen ist, ist dieser Schwellenwert von 50 % möglicherweise nicht geeignet. Wenn das Modell beispielsweise dazu tendiert, häufiger Bäume als Wandernde zu erkennen, also z. B. 10 % mehr Bäume als gewünscht, sollten Sie den Entscheidungswert entsprechend anpassen.

Auffrischung zu Entscheidungsmatrizen

Entscheidungsmatrizen sind eine hervorragende Möglichkeit, um zu bewerten, welche Fehler ein Modell macht. So erhalten Sie True-Positive-, True-Negative-, False-Positive- und False-Negative-Rate (TP, TN, FP, FN).

Diagram showing a confusion matrix of true positives, true negatives, false positives, and false negatives.

Aus dieser Wahrheitsmatrix können einige nützliche Merkmale berechnet werden. Diese beiden Merkmale werden häufig verwendet:

  • True-Positive-Rate (Empfindlichkeit): Gibt an, wie oft "True"-Bezeichnungen korrekt als "True" identifiziert werden, beispielsweise wie oft das Modell "Wandernde*r" vorhersagt, wenn das gezeigte Beispiel tatsächlich ein oder eine Wandernde*r ist
  • False-Positive-Rate (Rate für falschen Alarm): Gibt an, wie oft "False"-Bezeichnungen fälschlicherweise als "True" identifiziert werden, beispielsweise wie oft das Modell "Wandernde*r" vorhersagt, wenn das gezeigte Beispiel tatsächlich ein Baum ist.

Aus den True-Positive- und False-Positive-Raten können Sie auf die Modellleistung schließen.

Nehmen Sie dieses Wandererszenario als Beispiel. Im Idealfall ist die True-Positive-Rate sehr hoch und die False-Positive-Rate sehr niedrig, da das bedeutet, dass das Modell Wandernde häufig korrekt erkennt und nur selten Bäume mit Wandernden verwechselt. Wenn die True-Positive-Rate und die False-Positive-Rate jedoch beide sehr hoch sind, ist das Modell unausgewogen. In diesem Fall erkennt es dann fast alle Objekte als Wandernde. Ein Modell sollte aber auch keine niedrige True-Positive-Rate aufweisen, denn dann würde es Wandernde als Bäume klassifizieren.

ROC-Kurven

Bei ROC-Kurven handelt es sich um Graphen, die True-Positive-Raten und False-Positive-Raten vergleichend darstellen.

Für Einsteiger können ROC-Kurven aus zwei Gründen verwirrend sein. Der erste Grund ist, dass Einsteiger*innen davon ausgehen, dass jedes Modell nur über je einen Wert für die True-Positive- und die True-Negative-Rate verfügt, sodass ein ROC-Plot folgendermaßen aussehen muss:

Receiver operator characteristic curve graph with one plot point.

Wenn Sie auch dieser Meinung sind, liegen Sie richtig. Ein trainiertes Modell erzeugt nur einen Punkt. Bedenken Sie jedoch, dass die Modelle über einen Schwellenwert von normalerweise 50 % verfügen. Dieser wird verwendet, um zu entscheiden, ob die Bezeichnung true (Wandernde*r) oder false (Baum) angewendet werden soll. Wenn Sie diesen Schwellenwert in 30 % ändern und die True-Positive- und False-Positive-Raten neu berechnen, erhalten Sie einen weiteren Punkt:

Receiver operator characteristic curve graph with two plot points.

Wenn Sie dies für Schwellenwerte zwischen 0 % und 100 % durchführen, erhalten Sie einen solchen Graphen:

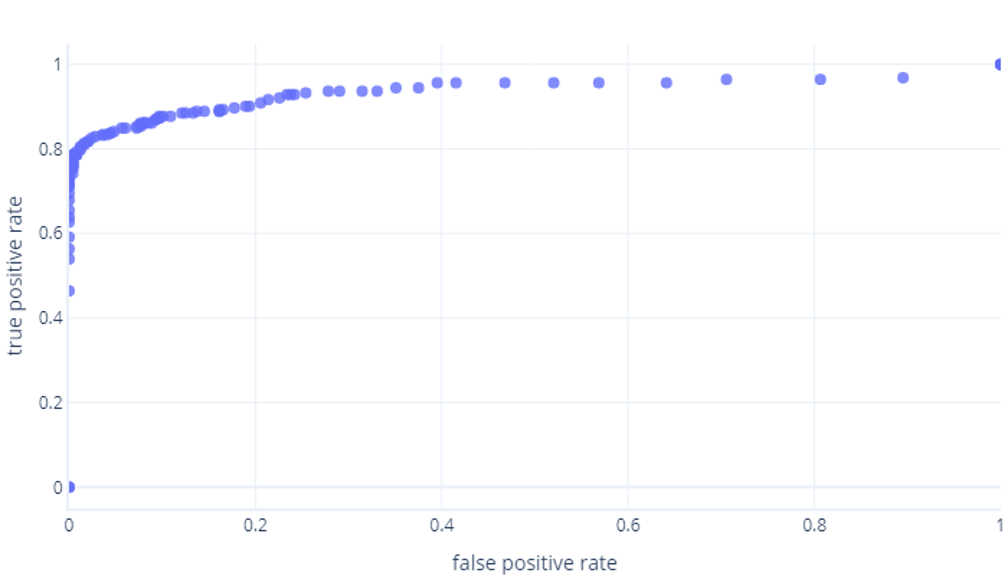
Receiver operator characteristic curve graph with a line of plot points.

Dieser wird üblicherweise als Linie dargestellt:

Receiver operator characteristic curve graph with a line in place of plot points for false positives.

Der zweite Grund, warum diese Graphen verwirrend sein können, ist der damit verbundene Fachjargon. Denken Sie daran, dass eine hohe True-Positive-Rate (Wanderer korrekt erkennen) und eine niedrige False-Positive Rate (Bäume nicht als Wanderer erkennen) angestrebt werden.

Receiver operator characteristic curve graph with a line in place of plot points for the rate of identifying trees as hikers.

Gute und schlechte ROC-Kurven

Der Unterschied zwischen einer guten und einer schlechten ROC-Kurve kann am besten in einer interaktiven Umgebung erklärt werden. Fahren Sie mit der nächsten Übung fort, um mehr über dieses Thema zu erfahren.