Was ist Regression?
Regression funktioniert, indem eine Beziehung zwischen Variablen in den Daten, die Merkmale (sogenannte Features) des beobachteten Objekts darstellen, und den Variablen, die vorhergesagt werden sollen (sogenannte Bezeichnungen) hergestellt wird.
Erinnern Sie sich daran, dass unser Unternehmen Fahrräder vermietet und die erwartete Anzahl der Vermietungen an einem bestimmten Tag vorhersagen möchte. In diesem Fall gehören zu den Features entsprechende Faktoren wie der Wochentag, der Monat usw., während die Bezeichnung die Anzahl der Fahrradvermietungen ist.
Beginnen Sie zum Trainieren des Modells mit einer Datenstichprobe, die die Features sowie bekannte Werte für die Bezeichnung enthält. In diesem Anwendungsfall benötigen Sie daher historische Daten, die Datumsangaben, Wetterbedingungen und die Anzahl der vermieteten Fahrräder enthalten.
Anschließend teilen Sie diese Datenstichprobe in zwei Teilmengen auf:
- Ein Trainingsdataset, auf das ein Algorithmus angewandt wird, in dem über eine Funktion die Beziehung zwischen den Featurewerten und den bekannten Bezeichnungswerten gekapselt wird.
- Ein Validierungs- oder Testdataset, das zum Auswerten des Modells verwendet werden kann, indem Vorhersagen für die Bezeichnung generiert und mit den tatsächlichen bekannten Bezeichnungswerten verglichen werden.
Wenn Sie zum Trainieren eines Modells Daten aus der Vergangenheit mit bekannten Bezeichnungswerten verwenden, bezeichnet man die Regression als überwachtes maschinelles Lernen.
Ein einfaches Beispiel
Sehen Sie sich ein einfaches Beispiel zur Funktionsweise von Trainings- und Evaluierungsprozess an. Angenommen, Sie vereinfachen das Szenario und verwenden nur ein einziges Feature (durchschnittliche Tagestemperatur), um die Bezeichnung für Fahrradvermietungen vorherzusagen.
Sie beginnen mit einigen Daten, die bekannte Werte für das Feature der durchschnittlichen Tagestemperatur und die Bezeichnung für Fahrradvermietungen enthalten.
| Temperatur | Vermietungen |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
Nun wählen wir fünf dieser Beobachtungen nach dem Zufallsprinzip aus und verwenden sie zum Trainieren eines Regressionsmodells. Wenn wir vom „Trainieren eines Modells“ sprechen, meinen wir damit, eine Funktion (eine mathematische Gleichung; nennen wir sie f) zu finden, die das Temperaturmerkmal (nennen wir es x) zur Berechnung der Anzahl der Vermietungen (nennen wir es y) verwenden kann. Anders ausgedrückt: Sie müssen die folgende Funktion definieren: f(x) = y.
Das Trainingsdataset sieht wie folgt aus:
| w | Y |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
Als Erstes zeichnen Sie die Trainingswerte für x und y in ein Diagramm ein:
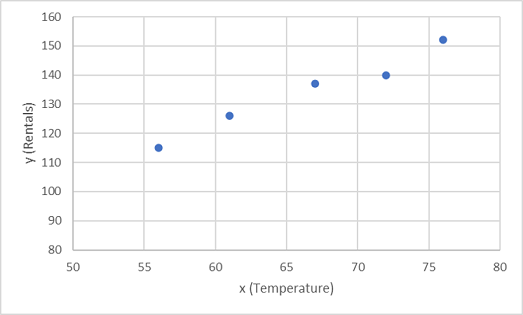
Nun müssen Sie diese Werte in eine Funktion einpassen, wobei einige zufällige Abweichungen möglich sind. Sie können wahrscheinlich erkennen, dass die gezeichneten Punkte eine fast gerade diagonale Linie bilden, oder anders ausgedrückt: Es besteht eine offensichtliche lineare Beziehung zwischen x und x. Das Ziel besteht also darin, eine lineare Funktion zu finden, die für die Datenstichprobe am besten geeignet ist. Es gibt verschiedene Algorithmen, mit denen diese Funktion bestimmt werden kann. Letztendlich geht es um eine gerade Linie mit einer minimalen Gesamtabweichung von den dargestellten Punkten, wie etwa im Folgenden:
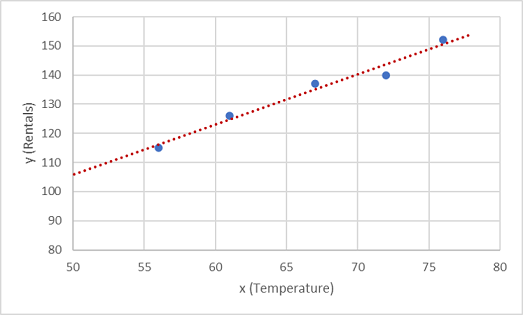
Die Linie stellt eine lineare Funktion dar, die mit jedem Wert von x verwendet werden kann, um die Steigung der Linie und ihren Schnittpunkt (mit der y-Achse, also bei x = 0) und damit y zu berechnen. Wenn Sie in diesem Fall die Linie nach links erweitern, stellen Sie Folgendes fest: Wenn x den Wert 0 aufweist, weist y ungefähr den Wert 20 auf. Der Wert von y steigt für jede weiter rechts liegende x-Einheit um 1,7, wodurch sich die Steigung der Linie ergibt. Daher können wir unsere f-Funktion 20 + 1,7x berechnen.
Nachdem die Vorhersagefunktion nun definiert ist, können Sie damit Bezeichnungen für die Validierungsdaten, die Sie zurückgehalten haben, vorhersagen und die vorhergesagten Werte (die in der Regel mit dem Symbol ŷ angeben werden) mit den tatsächlichen bekannten y-Werten vergleichen.
| x | Y | ŷ |
|---|---|---|
| 82 | 156 | 159,4 |
| 54 | 114 | 111,8 |
| 62 | 129 | 125,4 |
Im Folgenden sind die Werte für y und ŷ im Vergleich dargestellt:
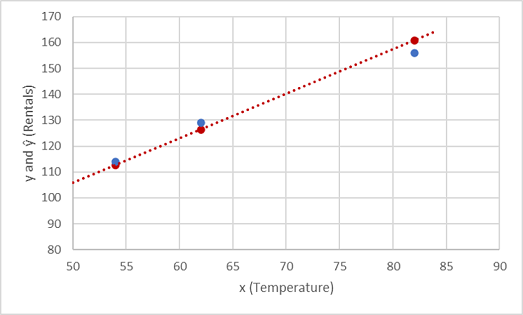
Die dargestellten Punkte, die sich auf dem Funktionsgraphen befinden, sind die vorhergesagten ŷ-Werte, die von der Funktion berechnet wurden, und die anderen Punkte sind die tatsächlichen y-Werte.
Es gibt verschiedene Möglichkeiten, die Abweichung zwischen den vorhergesagten und den tatsächlichen Werten zu messen. Sie können anhand dieser Metriken auswerten, wie gut die Vorhersagen des Modells sind.
Hinweis
Maschinelles Lernen basiert auf Statistiken und mathematischen Berechnungen, und es ist wichtig, bestimmte Begriffe zu kennen, die von Statistikern und Mathematikern (und damit auch von Data Scientists) verwendet werden. Sie können sich den Unterschied zwischen einem vorhergesagten Bezeichnungswert und dem tatsächlichen Bezeichnungswert als ein Fehlermaß vorstellen. In der Praxis basieren die „tatsächlichen“ Werte jedoch auf Beobachtungen an Stichproben (die selbst möglicherweise einer zufälligen Abweichung unterliegen können). Um zu verdeutlichen, dass ein vorhergesagter Wert (ŷ) mit einem beobachteten Wert (y) verglichen wird, wird der Unterschied zwischen diesen Werten als Residuen bezeichnet. Sie können die Residuen für alle Validierungsdatenvorhersagen zusammenfassen, um den Gesamtverlust des Modells als Maß für die Vorhersageleistung zu berechnen.
Eine der gängigsten Möglichkeiten für das Messen des Verlusts besteht darin, die einzelnen Residuen zu quadrieren, die Quadrate zu addieren und den Mittelwert zu berechnen. Das Quadrieren der Residuen bildet die Basis für die Berechnung der absoluten Werte (wobei außer Acht bleibt, ob der Unterschied negativ oder positiv ist) und bietet bei größeren Unterschiede eine stärkere Gewichtung. Diese Metrik wird als mittlere quadratische Abweichung bezeichnet.
Für die Validierungsdaten in diesem Beispiel sieht die Berechnung wie folgt aus:
| j | ŷ | y - ŷ | (y - ŷ)2 |
|---|---|---|---|
| 156 | 159,4 | -3,4 | 11,56 |
| 114 | 111,8 | 2.2 | 4.84 |
| 129 | 125,4 | 3.6 | 12,96 |
| Sum | ∑ | 29,36 | |
| Mittelwert | x̄ | 9,79 |
Der Verlust für dieses Modell beträgt daher basierend auf der MQA-Metrik (mittlere quadratische Abweichung) 9,79.
Ist das jetzt gut? Das ist schwierig zu beantworten, da der MQA-Wert nicht in einer aussagekräftigen Maßeinheit angegeben ist. Es ist zumindest eine Beziehung erkennbar: Je niedriger der Wert ist, desto geringer ist der Verlust des Modells, und desto besser ist daher auch die Vorhersage. Damit bildet der Wert eine nützliche Metrik zum Vergleichen zweier Modelle und zum Ermitteln des Modells mit der besseren Leistung.
Manchmal ist es sinnvoller, den Verlust in der gleichen Maßeinheit wie den vorhergesagten Bezeichnungswert selbst auszudrücken. In diesem Fall ist das die Anzahl der Vermietungen. Dazu berechnen Sie die Quadratwurzel des MSE-Werts. Daraus ergibt sich eine Metrik, die wenig überraschend als mittlere quadratische Gesamtabweichung (RMSE) bekannt ist.
√9,79 = 3,13
Die mittlere quadratische Gesamtabweichung dieses Modells gibt also an, dass der Verlust knapp über 3 liegt. Diese Zahl können Sie so interpretieren, dass falsche Vorhersagen im Durchschnitt um ungefähr drei Vermietungen daneben liegen.
Es gibt viele weitere Metriken, mit denen der Verlust in einer Regression gemessen werden kann. So ist z. B. R2 (R-Quadrat) (manchmal als Bestimmungskoeffizient bezeichnet) die Korrelation zwischen x und y zum Quadrat. Dies ergibt einen Wert zwischen 0 und 1, der die Größe der Abweichung misst, die durch das Modell erklärt werden kann. Im Allgemeinen gilt: Je näher der Wert an 1 ist, desto besser sind die Vorhersagen des Modells.