Was ist Regression?

Abgeschlossen

Die Regression ist ein einfaches, gängiges und äußerst nützliches Datenanalyseverfahren, das umgangssprachlich als „Erstellen einer Linie“ bezeichnet wird. In ihrer einfachsten Form erstellt die Regression eine gerade Linie zwischen einer Variablen (Feature) und einer anderen (Bezeichnung). In komplizierteren Fällen können per Regression nicht lineare Beziehungen zwischen einer einzelnen Bezeichnung und mehreren Merkmalen ermittelt werden.

Einfache lineare Regression

Die einfache lineare Regression modelliert eine lineare Beziehung zwischen einem einzelnen Feature und einer normalerweise fortlaufenden Bezeichnung, sodass das Feature die Bezeichnung vorhersagen kann. Grafisch dargestellt sieht dies ungefähr wie folgt aus:

Die einfache lineare Regression verfügt über zwei Parameter: einen Achsenabschnittparameter (c), der den Wert angibt, den die Bezeichnung beim Wert Null für das Feature hat, und einen Steigungsparameter (m), der angibt, um welchen Wert sich die Bezeichnung für jede 1-Punkt-Erhöhung des Features erhöht.

Mathematisch ausgedrückt ist dies einfach:

y=mx+c

Hierbei steht y für Ihre Bezeichnung und x für Ihr Feature.

Wenn wir in unserem Szenario beispielsweise versuchen, anhand des Alters vorherzusagen, welche Patienten eine aufgrund von Fieber erhöhte Körpertemperatur aufweisen, erhalten wir das folgende Modell:

Temperatur=m*Alter+c

Darüber hinaus müssen wir während des Erstellungsvorgangs die Werte für m und c ermitteln. Wenn wir m = 0,5 und c = 37 ermitteln, können wir dies wie folgt visualisieren:

Dies würde bedeuten, dass die Körpertemperatur mit jedem Altersjahr um 0,5 °C ansteigt, wobei der Startpunkt bei 37 °C liegt.

Anpassen der linearen Regression

Normalerweise verwenden wir vorhandene Bibliotheken, um Regressionsmodelle anzupassen. Bei der Regression soll normalerweise die Linie ermittelt werden, die zur geringsten Fehlermenge führt. Mit „Fehler“ ist hier der Unterschied zwischen dem tatsächlichen Datenpunktwert und dem vorhergesagten Wert gemeint. In der folgenden Abbildung gibt die schwarze Linie beispielsweise den Fehler zwischen der Vorhersage (rote Linie) und einem tatsächlichen Wert (Punkt) an.

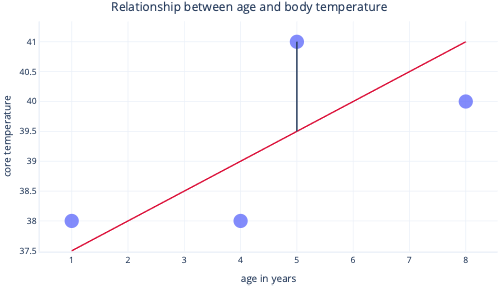
Wenn wir uns diese Punkte auf einer y-Achse ansehen, wird deutlich, dass der Vorhersagewert 39,5 und der tatsächliche Wert 41 ist.

Daher beträgt der Fehlerwert des Modells für diesen Datenpunkt 1,5.

Am häufigsten passen wir ein Modell an, indem wir die Quadratsumme der Residuen minimieren. Dies bedeutet, dass die folgende Berechnung der Kostenfunktion verwendet wird:

1. Berechnen der Differenz zwischen den tatsächlichen und vorhergesagten Werten (wie oben) für jeden Datenpunkt
2. Quadrieren dieser Werte
3. Berechnen der Summe (bzw. des Mittelwerts) dieser quadrierten Werte

Dieser Quadrierungsschritt bedeutet, dass nicht alle Punkte gleichmäßig zur Linie beitragen: Für Ausreißer – also Punkte, die aus dem erwarteten Muster herausfallen – liegt der Fehlerwert unverhältnismäßig viel höher, und dies kann sich auf die Position der Linie auswirken.

Vorteile der Regression

Regressionsverfahren verfügen über viele Vorteile, die komplexere Modelle nicht aufweisen.

Gute Vorhersagbarkeit und Interpretierbarkeit

Regressionen sind leicht zu interpretieren, weil damit einfache mathematische Gleichungen beschrieben werden, die häufig als Graph dargestellt werden können. Komplexere Modelle werden häufig als Blackbox-Lösungen bezeichnet, weil schwer zu verstehen ist, wie sie Vorhersagen treffen oder sich bei bestimmten Eingaben verhalten.

Einfache Extrapolation

Regressionen erleichtern die Extrapolation, also das Treffen von Vorhersagen für Werte außerhalb des Bereichs unseres Datasets. Im obigen Beispiel lässt sich beispielsweise leicht abschätzen, dass ein neunjähriger Hund eine Körpertemperatur von 40,5 °C hat. Bei der Extrapolation sollte immer mit Bedacht vorgegangen werden: Dieses Modell würde vorhersagen, dass die Körpertemperatur eines neunzigjährigen Hunds schon fast Wasser zum Kochen bringen würde.

Optimale Anpassung ist normalerweise garantiert

Für die meisten Machine Learning-Modelle wird das Gradientenabstiegsverfahren genutzt, um Modelle anzupassen. Dies umfasst die Optimierung des Algorithmus für das Gradientenabstiegsverfahren, bei dem es aber keine Garantie gibt, dass eine optimale Lösung gefunden werden kann. Im Gegensatz hierzu benötigt die lineare Regression, bei der die Quadratsumme als Kostenfunktion verwendet wird, kein iteratives Gradientenabstiegsverfahren. Stattdessen können ausgeklügelte mathematische Verfahren genutzt werden, um die optimale Position für die zu platzierende Linie zu berechnen. Eine Beschreibung der mathematischen Hintergründe würde den Rahmen dieses Moduls sprengen. Es ist aber hilfreich zu wissen, dass (sofern der Umfang der Stichprobe nicht zu groß ist) bei der linearen Regression nicht besonders auf den Anpassungsprozess geachtet werden muss und die optimale Lösung garantiert ist.