Transformationsübersicht

Matrixtransformationen übernehmen viele grundlegende mathematische Operationen der 3D-Grafik.

Die Geometriepipeline akzeptiert Scheitelpunkte als Eingabe. Das Transformationsmodul wendet die Welt-, Ansichts- und Projektionstransformationen auf die Eckpunkte an, schneidet das Ergebnis und übergibt alles an den Rasterizer.

Transformation und Raum	BESCHREIBUNG
Modellkoordinaten im Modellraum	An der Spitze der Pipeline werden die Scheitelpunkte eines Modells relativ zu einem lokalen Koordinatensystem festgelegt. Dies ist ein lokaler Ursprung und eine Ausrichtung. Diese Ausrichtung von Koordinaten wird häufig als Modellraum bezeichnet. Einzelne Koordinaten werden als Modellkoordinatengenannt.
Welttransformation in den Weltraum	In der ersten Phase der Geometriepipeline werden die Vertizes eines Modells von ihrem lokalen Koordinatensystem in ein Koordinatensystem transformiert, das von allen Objekten in einer Szene verwendet wird. Der Prozess der Neuausrichtung der Scheitelpunkte wird als Welttransformationbezeichnet, die von Modellraum in eine neue Ausrichtung, die als Welt-Raumbezeichnet wird, umgewandelt wird. Jeder Scheitelpunkt im Weltraum wird mit Weltkoordinatendeklariert.
Ansichtstransformation in den Ansichtsraum (Kameraraum)	In der nächsten Phase orientieren sich die Scheitelpunkte, die Ihre 3D-Welt beschreiben, in Bezug auf eine Kamera. Das heißt, Ihre Anwendung wählt einen Blickpunkt für die Szene aus, und Weltraumkoordinaten werden verschoben und um die Kameraansicht gedreht, wodurch der Weltraum in den Ansichtsbereich umgewandelt wird (auch als Kamerabereich bezeichnet). Dies ist die Ansichtstransformation, die vom Weltbereich in den Ansichtsbereich konvertiert wird.
Projektionstransformation in Projektionsraum	Die nächste Stufe ist die -Projektionstransformation, die den Ansichtsraum in den Projektionsraum überführt. In diesem Teil der Pipeline werden Objekte in der Regel im Verhältnis zu ihrer Entfernung vom Betrachter skaliert, um der Szene die Illusion der Tiefe zu verleihen; nahe Objekte werden so gestaltet, dass sie größer als entfernte Objekte erscheinen. Aus Gründen der Einfachheit bezieht sich diese Dokumentation auf den Raum, in dem Scheitelpunkte nach der Projektionstransformation als Projektionsraumvorhanden sind. Einige Grafikbücher beziehen sich möglicherweise auf den Projektionsraum als homogenen Raum nach der Perspektive. Nicht alle Projektionstransformationen skalieren die Größe von Objekten in einer Szene. Eine Projektion wie dies wird manchmal als affine oder orthogonale Projektionbezeichnet.
Clipping im Bildschirmraum	Im letzten Teil der Pipeline werden alle Scheitelpunkte, die auf dem Bildschirm nicht sichtbar sind, ausgeschlossen, sodass der Rasterizer nicht die Zeit in Anspruch nimmt, um die Farben und die Schattierung für Objekte zu berechnen, die nie zu sehen sind. Dieser Prozess wird als Clippingbezeichnet. Nach dem Clipping werden die verbleibenden Scheitelpunkte entsprechend den Viewport-Parametern skaliert und in Bildschirmkoordinaten konvertiert. Die resultierenden Scheitelpunkte, die beim Rastern der Szene auf dem Bildschirm angezeigt werden, sind in Bildschirmbereichvorhanden.

 

Transformationen werden verwendet, um die Objektgeometrie von einem Koordinatenbereich in einen anderen zu konvertieren. Direct3D verwendet Matrizen zum Ausführen von 3D-Transformationen. Matrizen erstellen 3D-Transformationen. Sie können Matrizen kombinieren, um eine einzelne Matrix zu erzeugen, die mehrere Transformationen umfasst.

Sie können Koordinaten zwischen Modellraum, Weltraum und Ansichtsraum transformieren.

• World Transform – Wandelt vom Modellraum in den Weltraum um.
• Ansichtstransformation – Wandelt aus dem Weltbereich in den Ansichtsbereich um.
• Projektionstransformation – Konvertiert vom Ansichtsbereich in den Projektionsbereich.

Matrixtransformationen

In Anwendungen, die mit 3D-Grafiken arbeiten, können Sie geometrische Transformationen verwenden, um folgendes auszuführen:

• Geben Sie den Standort eines Objektes relativ zu einem anderen Objekt an.
• Drehen und Größenanpassung von Objekten.
• Ändern Sie Ansichtspositionen, Richtungen und Perspektiven.

Sie können einen beliebigen Punkt (x,y,z) in einen anderen Punkt (x', y', z') umwandeln, indem Sie eine 4x4-Matrix verwenden, wie in der folgenden Formel dargestellt.

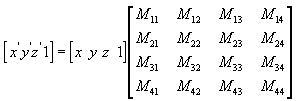
Führen Sie die folgenden Formeln für (x, y, z) und die Matrix aus, um den Punkt (x', y', z') zu erzeugen.

Die gängigsten Transformationen sind Übersetzung, Drehung und Skalierung. Sie können die Matrizen kombinieren, die diese Effekte in einer einzigen Matrix erzeugen, um mehrere Transformationen gleichzeitig zu berechnen. Sie können beispielsweise eine einzelne Matrix erstellen, um eine Reihe von Punkten zu übersetzen und zu drehen.

Matrizen werden in Zeilen- und Spaltenreihenfolge geschrieben. Eine Matrix, die Scheitelpunkte auf jeder Achse gleichmäßig skaliert, die als einheitliche Skalierung bezeichnet wird, wird mithilfe der mathematischen Schreibweise durch die folgende Matrix dargestellt.

In C++ deklariert Direct3D Matrizen als zweidimensionales Array mit einer Matrixstruktur. Das folgende Beispiel zeigt, wie sie eine D3DMATRIX Struktur initialisieren, die als einheitliche Skalierungsmatrix (Skalierungsfaktor "s") fungiert.

D3DMATRIX scale = {
    5.0f,            0.0f,            0.0f,            0.0f,
    0.0f,            5.0f,            0.0f,            0.0f,
    0.0f,            0.0f,            5.0f,            0.0f,
    0.0f,            0.0f,            0.0f,            1.0f
};

Übersetzen

Die folgende Formel übersetzt den Punkt (x, y, z) in einen neuen Punkt (x', y', z').

Sie können manuell eine Übersetzungsmatrix in C++ erstellen. Das folgende Beispiel zeigt den Quellcode für eine Funktion, die eine Matrix zum Übersetzen von Scheitelpunkten erstellt.

D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
    D3DXMATRIX ret;

    D3DXMatrixIdentity(&ret);
    ret(3, 0) = dx;
    ret(3, 1) = dy;
    ret(3, 2) = dz;
    return ret;
}    // End of Translate

Skala

Die folgende Formel skaliert den Punkt (x, y, z) um beliebige Werte in der x-, y- und z-Richtung auf einen neuen Punkt (x', y', z').

Drehen

Die hier beschriebenen Transformationen gelten für linkshändige Koordinatensysteme und unterscheiden sich daher möglicherweise von Transformationsmatrizen, die Sie an anderer Stelle gesehen haben.

Die folgende Formel dreht den Punkt (x, y, z) um die X-Achse, wodurch ein neuer Punkt (x', y', z') erzeugt wird.

Die folgende Gleichung dreht den Punkt um die Y-Achse.

Die folgende Formel dreht den Punkt um die Z-Achse.

In diesen Beispielmatrizen steht der griechische Buchstabe Theta für den Drehwinkel in Bogenmaßen. Winkel werden im Uhrzeigersinn gemessen, wenn man entlang der Drehachse in Richtung Ursprung blickt.

Der folgende Code zeigt eine Funktion zum Umgang mit der Drehung um die X-Achse.

    // Inputs are a pointer to a matrix (pOut) and an angle in radians.
    float sin, cos;
    sincosf(angle, &sin, &cos);  // Determine sin and cos of angle

    pOut->_11 = 1.0f; pOut->_12 =  0.0f;   pOut->_13 = 0.0f; pOut->_14 = 0.0f;
    pOut->_21 = 0.0f; pOut->_22 =  cos;    pOut->_23 = sin;  pOut->_24 = 0.0f;
    pOut->_31 = 0.0f; pOut->_32 = -sin;    pOut->_33 = cos;  pOut->_34 = 0.0f;
    pOut->_41 = 0.0f; pOut->_42 =  0.0f;   pOut->_43 = 0.0f; pOut->_44 = 1.0f;

    return pOut;
}

Verketten von Matrizen

Ein Vorteil der Verwendung von Matrizen besteht darin, dass Sie die Effekte von zwei oder mehr Matrizen kombinieren können, indem Sie sie multiplizieren. Dies bedeutet, dass Sie zwei Matrizen nicht anwenden müssen, um ein Modell zu drehen und es dann an einen beliebigen Ort zu verschieben. Stattdessen multiplizieren Sie die Rotations- und Übersetzungsmatrizen, um eine zusammengesetzte Matrix zu erzeugen, die alle ihre Effekte enthält. Dieser Prozess, der als Matrixverkettung bezeichnet wird, kann mit der folgenden Formel geschrieben werden.

In dieser Gleichung ist C die zusammengesetzte Matrix, die erstellt wird, und M₁ bis Mₙ sind die einzelnen Matrizen. In den meisten Fällen werden nur zwei oder drei Matrizen verkettet, aber es gibt keine Begrenzung.

Die Reihenfolge, in der die Matrixmultiplikation durchgeführt wird, ist entscheidend. Die vorangehende Formel gibt die Links-nach-rechts-Regel der Matrixverkettung wieder. Das heißt, die sichtbaren Effekte der Matrizen, die Sie zum Erstellen einer zusammengesetzten Matrix verwenden, treten in der Reihenfolge von links nach rechts auf. Im folgenden Beispiel wird eine typische Weltmatrix gezeigt. Stellen Sie sich vor, Sie erstellen die Weltmatrix für eine stereotypische fliegende Untertasse. Wahrscheinlich möchten Sie die fliegende Untertasse um ihre eigene Achse drehen - die Y-Achse des Modellraums - und sie an eine andere Stelle in Ihrer Szene verschieben. Um diesen Effekt zu erreichen, erstellen Sie zuerst eine Drehungsmatrix, und multiplizieren Sie sie dann mit einer Übersetzungsmatrix, wie in der folgenden Formel dargestellt.

In dieser Formel ist R_y eine Matrix zur Drehung um die y-Achse, und T_w ist eine Translation zu einer Position in Weltkoordinaten.

Die Reihenfolge, in der Sie die Matrizen multiplizieren, ist wichtig, da im Gegensatz zum Multiplizieren von zwei Skalarwerten die Matrixmultiplikation nicht kommutativ ist. Das Multiplizieren der Matrizen in der entgegengesetzten Reihenfolge hat die visuelle Wirkung, die fliegende Untertasse in ihre Weltraumposition zu übersetzen und dann um den Weltursprung herum zu drehen.

Unabhängig davon, welche Art von Matrix Sie erstellen, denken Sie an die Regel von links nach rechts, um sicherzustellen, dass Sie die erwarteten Effekte erzielen.

Verwandte Themen

Wandelt um