Anwenden von Transformationen in Direct2D

In Drawing with Direct2D haben wir gesehen, dass die ID2D1RenderTarget::FillEllipse-Methode eine Ellipse zeichnet, die an der X- und Y-Achse ausgerichtet ist. Aber angenommen, Sie möchten eine aus einem Winkel geneigte Ellipse zeichnen?

Mithilfe von Transformationen können Sie ein Shape auf die folgende Weise ändern.

• Drehen um einen Punkt.
• Skalierung.
• Übersetzung (Verschiebung in X- oder Y-Richtung).
• Schiefe (auch als Scherung bezeichnet).

Eine Transformation ist ein mathematischer Vorgang, der eine Reihe von Punkten einem neuen Satz von Punkten zuordnet. Das folgende Diagramm zeigt z. B. ein Dreieck, das um den Punkt P3 gedreht wurde. Nachdem die Drehung angewendet wurde, wird der Punkt P1 auf P1' abgebildet, der Punkt P2 wird auf P2' abgebildet, und der Punkt P3 wird auf sich selbst abgebildet.

Transformationen werden mithilfe von Matrizen implementiert. Sie müssen jedoch nicht die Mathematik der Matrizen verstehen, um sie zu verwenden. Wenn Sie mehr über die Mathematik erfahren möchten, lesen Sie Anhang: Matrixtransformationen.

Rufen Sie zum Anwenden einer Transformation in Direct2D die ID2D1RenderTarget::SetTransform-Methode auf. Diese Methode verwendet eine D2D1_MATRIX_3X2_F Struktur, die die Transformation definiert. Sie können diese Struktur initialisieren, indem Sie Methoden für die D2D1::Matrix3x2F-Klasse aufrufen. Diese Klasse enthält statische Methoden, die eine Matrix für jede Art von Transformation zurückgeben:

• Matrix3x2F::Drehung
• Matrix3x2F::Scale
• Matrix3x2F::Translation
• Matrix3x2F::Skew

Der folgende Code wendet beispielsweise eine Drehung von 20 Grad um den Punkt an (100, 100).

pRenderTarget->SetTransform(
    D2D1::Matrix3x2F::Rotation(20, D2D1::Point2F(100,100)));

Die Transformation wird auf alle späteren Zeichnungsvorgänge angewendet, bis Sie SetTransform erneut aufrufen. Um die aktuelle Transformation zu entfernen, rufen Sie SetTransform mit der Identitätsmatrix auf. Rufen Sie zum Erstellen der Identitätsmatrix die Matrix3x2F::Identity-Funktion auf.

pRenderTarget->SetTransform(D2D1::Matrix3x2F::Identity());

Zeichnen von Uhrhändigen

Lassen Sie uns Transformationen verwenden, indem wir unser Circle-Programm in eine analoge Uhr konvertieren. Dazu können wir Linien für die Hände hinzufügen.

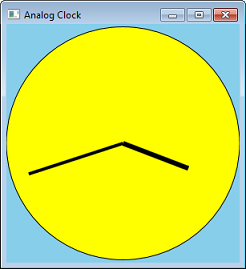
Anstatt die Koordinaten für die Linien zu berechnen, können wir den Winkel berechnen und dann eine Drehungstransformation anwenden. Der folgende Code zeigt eine Funktion, die einen Uhrzeiger zeichnet. Der fAngle-Parameter gibt den Winkel der Hand in Grad an.

void Scene::DrawClockHand(float fHandLength, float fAngle, float fStrokeWidth)
{
    m_pRenderTarget->SetTransform(
        D2D1::Matrix3x2F::Rotation(fAngle, m_ellipse.point)
            );

    // endPoint defines one end of the hand.
    D2D_POINT_2F endPoint = D2D1::Point2F(
        m_ellipse.point.x,
        m_ellipse.point.y - (m_ellipse.radiusY * fHandLength)
        );

    // Draw a line from the center of the ellipse to endPoint.
    m_pRenderTarget->DrawLine(
        m_ellipse.point, endPoint, m_pStroke, fStrokeWidth);
}

Dieser Code zeichnet eine vertikale Linie, beginnend vom Mittelpunkt des Zifferblatts und endend am Punkt endPoint. Die Linie wird um die Mitte der Ellipse gedreht, indem eine Drehungstransformation angewendet wird. Der Mittelpunkt für die Drehung ist der Mittelpunkt der Ellipse, die das Zifferblatt bildet.

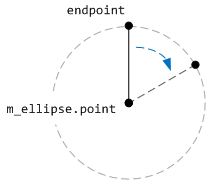
Der folgende Code zeigt, wie das gesamte Zifferblatt gezeichnet wird.

void Scene::RenderScene()
{
    m_pRenderTarget->Clear(D2D1::ColorF(D2D1::ColorF::SkyBlue));

    m_pRenderTarget->FillEllipse(m_ellipse, m_pFill);
    m_pRenderTarget->DrawEllipse(m_ellipse, m_pStroke);

    // Draw hands
    SYSTEMTIME time;
    GetLocalTime(&time);

    // 60 minutes = 30 degrees, 1 minute = 0.5 degree
    const float fHourAngle = (360.0f / 12) * (time.wHour) + (time.wMinute * 0.5f);
    const float fMinuteAngle =(360.0f / 60) * (time.wMinute);

    DrawClockHand(0.6f,  fHourAngle,   6);
    DrawClockHand(0.85f, fMinuteAngle, 4);

    // Restore the identity transformation.
    m_pRenderTarget->SetTransform( D2D1::Matrix3x2F::Identity() );
}

Sie können das vollständige Visual Studio-Projekt aus dem Direct2D-Clock-Beispiel herunterladen. (Gerade zum Spaß fügt die Downloadversion dem Uhrblatt einen radialen Farbverlauf hinzu.)

Kombinieren von Transformationen

Die vier grundlegenden Transformationen können kombiniert werden, indem zwei oder mehr Matrizen multipliziert werden. Der folgende Code kombiniert beispielsweise eine Drehung mit einer Translation.

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(20);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(40, 10);

pRenderTarget->SetTransform(rot * trans);

Die Matrix3x2F-Klasse stellt operator*() für die Matrixmultiplizierung bereit. Die Reihenfolge, in der Sie die Matrizen multiplizieren, ist wichtig. Das Festlegen einer Transformation (M × N) bedeutet "M zuerst anwenden, gefolgt von N". So folgt beispielsweise die Drehung, gefolgt von übersetzung:

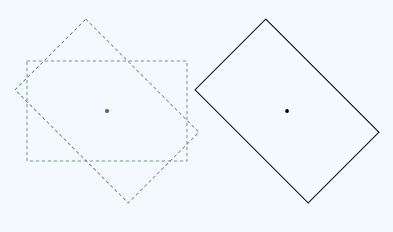
Hier ist der Code für diese Transformation:

const D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
const D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(rot * trans);

Vergleichen Sie diese Transformation nun mit einer Transformation in umgekehrter Reihenfolge, bei der erst die Übersetzung und dann die Drehung erfolgt.

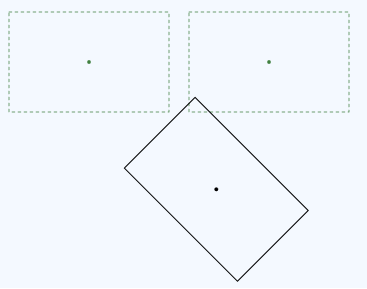
Die Drehung erfolgt um die Mitte des ursprünglichen Rechtecks. Hier ist der Code für diese Transformation.

D2D1::Matrix3x2F rot = D2D1::Matrix3x2F::Rotation(45, center);
D2D1::Matrix3x2F trans = D2D1::Matrix3x2F::Translation(x, 0);
pRenderTarget->SetTransform(trans * rot);

Wie Sie sehen können, sind die Matrizen identisch, aber die Reihenfolge der Vorgänge hat sich geändert. Dies geschieht, da die Matrixmultiplikation nicht kommutativ ist: M × N ≠ N × M.

Weiter

Anhang: Matrixtransformationen