WCS Gamut Map Model Profile Schema und Algorithmen

• Übersicht
• Profilarchitektur des Gamut-Kartenmodells
• Generation der Gamut-Grenze
• Das GMMP-Schema
• Die GMMP-Schemaelemente
• GamutMapModel-
  • Namespace-
  • Version
  • Dokumentation
  • DefaultBaselineGamutMapModel-Typ
  • PlugInGamutMapType
  • ExtensionType-
• die GMMP-Baselinealgorithmen
• Ausrichten der neutralen Achsen
  • Minimale Farbdifferenz (MinCD)
  • BasicPhoto-
  • Übersicht
  • Der Fall einer einzelnen Gamut-Shell
  • black enhancement
  • Der Fall von dualen Gamut-Shells
  • Gründe für Änderungen aus den Empfehlungen von CIE TC8-03
  • Hue-Zuordnung
• Beschreibung der Gamutgrenze und Gamut Shell-Algorithmen
  • Triangulation der Gamut-Grenze
  • Begrenzungslinienelemente
  • Gamut-Vorgang: CheckGamut
  • Full Hue Plane: Schneiden Sie
  • Gamut Operation: CheckGamut (fortsetzung)
  • Minimale Farbdifferenz-Gamutzuordnung
  • Farbtonglättung
  • Festlegen von Primaren und Secondaries in der Beschreibung der Gamut-Grenze
  • Festlegen der neutralen Achse in der Beschreibung der Gamut-Grenze
• Verwandte Themen

Überblick

Dieses Schema wird verwendet, um den Inhalt eines Gamut-Kartenmodellprofils (GMMP) anzugeben. Die zugeordneten Basisalgorithmen werden im folgenden Thema beschrieben.

Das grundlegende GMMP-Schema besteht aus allgemeinen Headerinformationen, einem optionalen Verweis auf ein bevorzugtes Gamut Map Model-Plug-In und Erweiterungstags.

Darüber hinaus stellt der GMMP explizite Informationen zum zielbezogenen Gamut-Kartenmodell bereit und stellt eine Richtlinie für das grundlegende Fallback-Gamut-Kartenmodell bereit, das verwendet werden soll, wenn das Zielmodell nicht verfügbar ist. Das Schema kann private Erweiterungsinformationen enthalten, enthält jedoch keine anderen zusätzlichen Informationen.

Architektur des Gamut-Kartenmodells

Das Sampling des Farbraums des Ausgabegeräts erfolgt durch Durchlaufen der Farbstoffe von 0,0 auf 1,0 mit einem Bruchschritt, akkumulieren alle Kombinationen der einzelnen Farbstoffe in jedem Schritt und anschließendes Konvertieren von Gerätefarbraum in Farbdarstellungsbereich mithilfe der DM::D eviceToColorimetricColors-Methode gefolgt von der CAM::ColorimetricToAppearanceColors-Methode. Im Folgenden sehen Sie ein Beispiel dafür, wie dies für RGB erfolgt.

For (red= 0.0; red <= 1.0; red += redStep) {

     For (green = 0.0; green <= 1.0; green += greenStep) {

          For (blue = 0.0; blue <= 1.0; blue += blueStep) {

               Colorants[0] = red; colorants[1] = green; colorants[2] = blue;

               pRGBDM->DeviceToColorimetricColors(1, colorants, &amp;XYZ);

               pCAM->ColorimetricToAppearanceColors(1, &amp;XYZ, &amp;JCh);

          }

     }

}

Generation der Gamut-Grenze

Es gibt drei Komponenten der Gamutgrenze: die Primar, die neutralen Proben und die Schalen. Die Primarwerte werden generiert, indem die Geräte primaries verwendet und die DeviceToColorimetric/ColorimetricToAppearance-Transformation angewendet wird. Die neutralen Proben werden durch Sampling des Farbraums des Geräts im neutralen Bereich erzeugt und dieselbe Transformation angewendet. Bei drei Farbgeräten (RGB oder CMY) werden die neutralen Proben so definiert, dass alle Farbstoffe gleich sind, z. B. R == G == B. Für CMYK werden die neutralen Proben mit C == M == Y == 0 definiert.

Die Faktoren, die die Daten beeinflussen, die zum Erstellen der Gamutgrenze verwendet werden, sind die Datenbeispiele (nur Basisgeräte) und die Anzeigebedingungen. Die Schrittgröße, die zum Ausführen des vollständigen Samplings des Farbraums (für Monitore und für plausible Shell) verwendet wird, ist eine interne Konstante und steht für externe Manipulationen nicht zur Verfügung. Wenn Sie die Anzeigebedingungen ändern, wird das Verhalten des Farbdarstellungsmodells (CAM) geändert und die Form der Gamutgrenze geändert, sodass Sie eine gamutgebundene Grenze generieren müssen, die an das Profil der Anzeigebedingungen gebunden ist. Wenn Beispieldaten verwendet werden, wie bei Basisdruckern und Aufnahmegeräten, haben die Beispiele eine menge Auswirkungen auf die Form der Referenzskala und wirken sich auf das Verhalten des Modells selbst aus.

Für Eingabegeräte wie Kameras und Scanner werden verschiedene Samplings verwendet, um die Referenzshell und die plausible Shell zu generieren. Die Referenzshell wird aus den Maßen generiert, die zum Initialisieren des Gerätemodells verwendet werden. Die plausible Shell wird ähnlich der vorherigen Abbildung für Ausgabegeräte generiert. Der Unterschied besteht darin, dass beim Eingeben eines typischen Ziels keine vollständig gesättigten Werte angezeigt werden (wobei R, G oder B = 255). Sie müssen die Verwendung des Gerätemodells extrapolieren, um diese Werte zu schätzen.

Das GMMP-Schema

<?xml version="1.0" encoding="UTF-8"?>
<xs:schema 
  xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
  xmlns:wcs="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes"
  targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"
  xmlns:xs="http://www.w3.org/2001/XMLSchema"
  elementFormDefault="qualified"
  attributeFormDefault="unqualified"
  blockDefault="#all"
  version="1.0">

  <xs:annotation>
    <xs:documentation>
      Gamut Map Model profile schema.
      Copyright (C) Microsoft. All rights reserved.
    </xs:documentation>
  </xs:annotation>

  <xs:import namespace="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes" />

  <xs:element name="GamutMapModel">
    <xs:complexType>
      <xs:sequence>
        <xs:element name="ProfileName" type="wcs:MultiLocalizedTextType"/>
        <xs:element name="Description" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="Author" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="DefaultBaselineGamutMapModel">
          <xs:simpleType>
            <xs:restriction base="xs:string">
              <xs:enumeration value="HPMinCD_Absolute"/>
              <xs:enumeration value="HPMinCD_Relative"/>
              <xs:enumeration value="SGCK"/>
              <xs:enumeration value="HueMap"/>
            </xs:restriction>
          </xs:simpleType>
        </xs:element>
        <xs:element name="PlugInGamutMapModel" minOccurs="0">
          <xs:complexType>
            <xs:sequence>
              <xs:any namespace="##other" processContents="skip"
                minOccurs="0" maxOccurs="unbounded" />
            </xs:sequence>
            <xs:attribute name="GUID" type="wcs:GUIDType" use="required"/>
          </xs:complexType>
        </xs:element>
      </xs:sequence>
      <xs:attribute name="ID" type="xs:string" use="optional" />
    </xs:complexType>
  </xs:element>
</xs:schema>

Die GMMP-Schemaelemente

GamutMapModel

Dieses Element ist eine Sequenz der folgenden Unterelemente:

1. ProfileName-Zeichenfolge,
2. DefaultBaselineGamutMapModel,
3. Optionale Beschreibungszeichenfolge,
4. Optionale Author-Zeichenfolge,
5. Optionales PlugInGamutMap und
6. Optionaler ExtensionType-Wert.

Überprüfungsbedingungen: Jedes Unterelement wird durch seinen eigenen Typ überprüft.

Namespace

xmlns:gmm="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"

targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/GamutMapModel"

Version

Version "1.0" mit der ersten Version von Windows Vista.

Überprüfungsbedingungen : 1.0 in Windows Vista. Versionen <2.0 sind ebenfalls gültig, um unterbrechungsfreie Änderungen am Format zu unterstützen.

Dokumentation

Schema des Gamut-Kartenmodellprofils.

Copyright (C) Microsoft. Alle Rechte vorbehalten.

Überprüfungsbedingungen: Jedes Unterelement wird durch seinen eigenen Typ überprüft.

DefaultBaselineGamutMapModel-Typ

UINT-Typ

Enumerationswerte:

"MinCD\_Absolute" "MinCD\_Relative" "SIG\_KNEE" "HueMap"

Überprüfungsbedingungen: Die Werte müssen einer der oben aufgeführten Enumerationen entsprechen.

PlugInGamutMapType

Dieses Element ist eine Sequenz einer GUID GUIDType und aller Unterelemente.

Überprüfungsbedingungen: Die GUID wird verwendet, um der GUID des GMM PlugIn DLL-Codes zu entsprechen. Es gibt maximal 100.000 benutzerdefinierte Unterelemente.

Erweiterungstyp

Dieses Element ist eine optionale Abfolge von Unterelementen.

Überprüfungsbedingungen: Maximal 100.000 Unterelemente können vorhanden sein.

Die GMMP-Basisalgorithmen

Ausrichten der Neutralachsen

Die meisten Gamut-Zuordnungsalgorithmen haben das Ziel, die neutrale Achse des Quellgeräts der neutralen Achse des Zielgeräts zuzuordnen: d. h. weiß geht zu Weiß, Schwarz zu Schwarz und Grau zu Grau. Dies wird teilweise behoben, indem die Lichtheit der Quellfarben entsprechend dem Lichtbereich des Zielgeräts skaliert wird. Aber das geht nicht vollständig auf das Problem an.

Es handelt sich um eine physische Eigenschaft der meisten Bildbildgeräte, die die Farbigkeit des Geräts weiß nicht genau mit der Farbigkeit des Geräts schwarz übereinstimmt. Beispielsweise hängt Monitorweiß von der Summe der Farbigkeiten und relativen Leuchtdichten der drei Primaren ab, während der Monitor schwarz von der Spiegelung der Anzeigeoberfläche abhängt. Druckerweiß hängt von der Farbigkeit des Papiers ab, während Drucker schwarz von der verwendeten Tinte oder Toner abhängt. Ein Darstellungsmodell, das das Gerät weiß genau der neutralen Achse des Darstellungsbereichs (Chroma genau gleich Null) zuordnet, wird das Gerät nicht schwarz zur neutralen Achse zuordnen. Da das Auge empfindlicher gegenüber Farbunterschieden ist, da die Lichtheit zunimmt, werden Midgraue als noch mehr Farbton als Geräteschwarz dargestellt. (Abbildung 1 veranschaulicht die Krümmung der neutralen Achsen in zwei Dimensionen. Tatsächlich bilden die neutralen Achsen eine komplexere Kurve in drei Dimensionen.)

Während die CAM voraussagt, dass diese Geräteneutralfarben farblich erscheinen, scheinen die tatsächlichen Beobachter dies zu kompensieren. Die meisten Menschen betrachten diese geräteneutralen Werte nicht als chromatisch. Für die meisten Gamut-Zuordnungsmodelle sollten Sie daher weiterhin quellneutrale Geräteneutrale zuordnen.

Um Quellneutralitäten geräteneutral zuzuordnen, passen Sie die Grenzen der Quell- und Zielskala und jedes Pixel an, wenn Sie den Gamutzuordnungsalgorithmus anwenden. Passen Sie zunächst jeden Wert in der Quellfarbe so an, dass die neutrale Achse des Quellgeräts auf der Hellheit der Quellfarbe direkt auf die neutrale Achse des Darstellungsbereichs fällt. (Siehe die linke Seite von Abbildung 1.) Passen Sie dann die Gamut-Begrenzungsbeschreibung des Zielgeräts so an, dass jede Farbe auf der neutralen Achse des Zielgeräts auf der Farbskala der Begrenzungsfarbe des Zielgeräts direkt auf die neutrale Achse des Darstellungsbereichs fällt. (Siehe die rechte Seite von Abbildung 1.)

Abbildung 1: Ausrichtung der dargestellten neutralen Achsen. Links: Anpassen von Quellpunkten relativ zur Neutralachse des Quellgeräts. Rechts: Anpassen der Beschreibung der Zielskalagrenze relativ zur Beschreibung der Zielskalagrenze.

Beachten Sie, dass Sie jeden Quellpixelwert relativ zur neutralen Achse an diesem Lichtwert anpassen. Dadurch wird sichergestellt, dass Quellgeräteneutrale auf die neutrale Achse des Darstellungsmodells fallen. Sie verschieben auch alle anderen Farben bei dieser Leichtigkeit um dieselbe Menge, sodass es keine Unterbrechungen in der Darstellung der Quellskala gibt. Sie müssen sich auf unterschiedlichen Lichtniveaus um unterschiedliche Mengen verschieben, da die Neutrale des Quellgeräts nicht auf den unterschiedlichen Lichtstärken gleich farblich dargestellt werden. Klar, das ist keine triviale Transformation.

Die Behandlung der Zielgerätewerte ist etwas schwieriger. Zunächst passen Sie die gesamte Zielskalagrenze auf ähnliche Weise an, aber relativ zur neutralen Zielachse des Zielgeräts. Dies ist in Abbildung 1 auf der rechten Seite dargestellt. Diese Anpassung stellt sicher, dass Quellgrauwerte den Zielgrauwerten zugeordnet werden. Dies ist der Raum, in dem die Gamut-Zuordnungsalgorithmen funktionieren.

Dieser Speicherplatz beschreibt jedoch nicht genau das wahre Verhalten des Zielgeräts. Sie müssen die Zuordnung umkehren, bevor die farbskala zugeordneten Farben an das Darstellungsmodell und das Zielgerätemodell übergeben werden. Alle zugeordneten Werte werden durch das Gegenteil des zuvor auf die neutrale Zielgeräteachse angewendeten Offsets versetzt. Dadurch wird die zielneutrale Achse dem ursprünglich durch die CAM dargestellten Wert zugeordnet. Dies gilt für die Gamutgrenze und alle Zwischenwerte.

Abbildung 2: Rückgängigmachen der Ausrichtung der neutralen Zielgeräteachse

Minimaler Farbunterschied (MinCD)

Minimaler Farbunterschied (MinCD) Relative und Absolute Versionen – entspricht der farbmetrischen Absicht von ICC.

Anmerkung

Das MinCD GMM eignet sich für die Zuordnung von Grafiken und Liniengrafiken mit "Logo"-Farben (Spotfarben), Logofarbverläufen mit einigen out-of-gamut-Farben und für die letzte Phase der Korrekturhilfetransformationen. Obwohl das MinCD GMM für fotografische Bilder verwendet werden kann, die sich vollständig innerhalb der Zielskala befinden, empfiehlt es sich nicht für das allgemeine Rendern von fotografischen Bildern. Die Zuordnung von Nicht-Gamut-Farben zu Farben auf der Ziel-Gamutoberfläche kann zu unerwünschten Artefakten führen, z. B. Ton oder Unregelmäßigkeiten bei flüssigen Farbverläufen, die die Gamutgrenze überschreiten. BasicPhoto wird für fotografische Bilder empfohlen. Wenn ein fotografisches oder kontones Bild eine andere Gamut-Zuordnung als BasicPhoto erfordert, sollte die Alternative sein, ein Plug-In-GMM zu erstellen, das diese Zuordnung implementiert, anstatt MinCD zu verwenden.

 

In-Gamut-Farben bleiben unverändert. Bei Nicht-Gamut-Farben werden Licht und Color angepasst, indem der Punkt im Zielbereich gefunden wird, der den minimalen Farbabstand von Out-of-Gamut-Eingabepunkten aufweist. Der Farbabstand wird im JCh-Raum berechnet. Sie gewichten jedoch den Abstand in Leichtigkeit (J) und den Abstand in Chroma (C) oder Farbton (h) unterschiedlich. Eine farbabhängige Gewichtsfunktion wird für den Abstand in Leichtigkeit verwendet, sodass das Gewicht für kleine Chroma und größer für große Chroma kleiner ist, bis eine Schwellen-Chroma erreicht wird, danach bleibt das Gewicht bei 1, d. h. das gleiche Gewicht wie abstand in Chroma oder Farbton. Dies folgt der empfohlenen Verwendung für CMC und CIEDE2000. Es gibt zwei Varianten: Relative Farbmetrik und absolute Farbmetrik.

Relative Farbmetrik: Zuerst richten Sie die Quell- und Zielneutralachsen wie zuvor beschrieben aus. Schneiden Sie dann die angepasste Quellfarbe an die angepasste Zielskalagrenze ab. (Siehe Abbildung 4. Chroma-Zuordnung entlang konstanter Leichtigkeit.) Aktualisieren Sie die Zielgerätewerte wie zuvor beschrieben. Bei einer monochromen Ziel-Gamutgrenze bedeutet der Farbfarbschnitt, dass der Farbfarbwert (C) auf Null (0,0) festgelegt ist.

absolute Farbmetrik: Dies ähnelt relativer Farbmetrik, jedoch ohne ausrichtung der Quell- und Zielneutralachse. Der Quellwert wird direkt auf die zielneutrale Achse zugeschnitten. Beachten Sie, dass das Verhalten identisch mit der relativen farbmetrischen Variante ist, wenn sowohl die Quell- als auch die Ziel-Gamut-Begrenzung monochrom sind; d. h., die Ausrichtung der neutralen Achsen erfolgt, und dann wird die Chroma auf Null abgeschnitten. Dadurch wird sichergestellt, dass eine angemessene Ausgabe erreicht wird, auch wenn sich die Medien und Farbstoffe erheblich unterscheiden.

Abbildung 3: MinCD-Clipping an die angepasste Gamut

BasicPhoto

Überblick

BasicPhoto – entspricht der bevorzugten ICC-, Bild- oder Wahrnehmungsabsicht.

Dieser Algorithmus ist eine Variante der farbabhängigen Sigmoidallichtzuordnung und cusp-Knieskalierung (SGCK), die von CIE TC8-03 in CIE156:2004 beschrieben wird. Dieser Variantenalgorithmus unterstützt Gamut-Grenzdeskriptoren (GBDs) mit dualen Gamut-Shells; d. h. GBDs mit einer Referenzshell und einer plausiblen Shell. Der SGCK-Algorithmus, der ursprünglich nur eine Gamut-Shell in der GBD annimmt, basiert auf dem SIG_KNEE Algorithmus (Braun 1999), der die sigmoidale Lichtzuordnung und Kniefunktionsskalierung von Braun und Fairchild (1999) umfasst, kombiniert mit der Chromaabhängigkeit von GCUSP (Morovic, 1998). Es hält wahrgenommene Farbtonkonstante, z. B. Farbtonwinkel in farbkorrekturen Jab, und verwendet eine generische (bildunabhängige) sigmoidale Helligkeitsskalierung, die auf eine farbabhängige Weise angewendet wird und eine 90 Prozent Kniefunktion Chroma. Die Variante skaliert entlang der Linien der konstanten Leichtigkeit.

Die Groß-/Kleinschreibung einer einzelnen Gamut-Shell

Es ist hilfreich, den Algorithmus zu überprüfen, wenn sowohl Quell- als auch Ziel-GBDs nur eine Gamut-Shell aufweisen. In diesem Fall besteht der Algorithmus aus den folgenden Berechnungen.

Führen Sie zunächst die anfängliche Lichtheitszuordnung mit der folgenden Formel aus:

(1)

dabei ist Jₒ die ursprüngliche Leichtigkeit und J_R ist die Leichtigkeit der Reproduktion.

(2)

Wenn die Quell-Gamutgrenze monochrom ist, wird der Farbwert für die Monochromgrenze aufgrund der ausrichtung der neutralen Achse null sein. Dies führt zu einem degeneraten Fall, in dem C gleich Null ist. In diesem Fall ist p_C- auf 1 festgelegt.

p_C ist ein farbabhängiger Gewichtungsfaktor (Morovic, 1998), der von der Color der Originalfarbe abhängt, C und J_S sind das Ergebnis der ursprünglichen Leichtigkeit, die mit einer sigmoidalen Funktion zugeordnet wird.

 

Um J_S (Braun und Fairchild, 1999) zu berechnen, wird zunächst eine eindimensionale Nachschlagetabelle (LUT) zwischen Original- und Reproduktionslichtwerten auf der Grundlage einer diskreten kumulierten Normalfunktion (S) eingerichtet.

(3)

wobei x ₀ und S die Mittel- und Standardabweichung der Normalverteilung bzw. i = 0,1,2 sind... mistm die Anzahl der in der LUT verwendeten Punkte. S_i ist der Wert der kumulierten Normalfunktion für i /m Prozent. Die Parameter hängen von der Leichtigkeit des schwarzen Punkts der Reproduktionsskala ab und können aus Tabelle 1 interpoliert werden. Einzelheiten zur Berechnung dieser Parameter finden Sie unter Braun und Fairchild (1999, S. 391).

J _minOut-

5.0

10,0

15,0

20.0

x ₀

53.7

56.8

58.2

60.6

S

43.0

40.0

35.0

34,5

Tabelle 1: Berechnung des BasicPhoto-Komprimierungsparameters

Um S als Lichtheitszuordnung LUT (S _LUT) zu verwenden, muss es zuerst in den Lichtbereich von [0,100] normalisiert werden. Die normalisierten Daten werden dann in den dynamischen Bereich des Zielgeräts skaliert, wie in Formel 4 dargestellt, wobei J_{min\ Out} und J_{max\ Out} sind die Werte der Leichtigkeit des schwarzen Punkts und des Weißen Punkts des Wiedergabemediums, beziehungsweise.

(4)

An dieser Stelle können die J S Werte aus dem S _LUT durch Interpolieren zwischen den m Punkt der entsprechenden J O'- und J S Werte abgerufen werden, die sie enthält, und die folgende Formel als Eingabe verwenden.

(5)

J _minIn ist der Lichtwert des schwarzen Punkts des ursprünglichen Mediums, J _maxIn ist der Lichtwert des ursprünglichen Mediums, und J _O ist die ursprüngliche Leichtigkeit. Für späteren Bezug können Sie durch S die sigmoidale Funktion bezeichnen, die in der soeben beschriebenen Weise definiert ist, wie in der folgenden Abbildung 4 dargestellt.

Abbildung 4: Chroma-Zuordnung entlang konstanter Leichtigkeit

Zweitens, wenn die Ziel-Gamutgrenze farbtisch ist, komprimieren Sie Chroma entlang der Linien der konstanten Leichtigkeit (l) und führen Sie die Komprimierung wie folgt aus.

(6)

wobei d den Abstand von E- auf ldarstellt;g stellt die mittlere Gamutgrenze dar; r stellt die Reproduktion dar; und o der ursprünglichen Abbildung 5.

Abbildung 5: Farb- und Lichtkomprimierung in BasicPhoto

Wenn die Grenze für die Zielskala monochrom ist, wird der Farbwert auf Null abgeschnitten.

Verwenden Sie drittens einen MinCD-Clip (weiter oben beschrieben), um restfehler zu beseitigen.

Schwarze Verbesserung

Der vorherige Algorithmus kann geändert werden, um das Schwarz zu verbessern, wenn es sich bei dem Ziel um ein Druckergerät handelt. Das Problem muss mit der Wahl von J_minOutzu tun haben, was normalerweise nicht der dunkelsten Farbe entspricht, die ein Drucker erzeugen kann.

Genauer gesagt ist die Farbe mit der höchsten Dichte, die durch die Platzierung von 100 Prozent Druckfarben (oder maximale mögliche Abdeckung, wenn GCR/Freihandbegrenzung wirksam ist) in der Regel nicht "neutral" im Farbdarstellungsbereich. Siehe Abbildung 6. Anders ausgedrückt: Wenn für das Zielgerät eine neutrale Mindestlichtstärke verwendet wird, wird der konstruierte Lichtmaßstabskalierung einer minimalen Lichtdichte zugeordnet, die nicht die höchste Dichte ist, die vom Drucker erreicht werden kann. Berücksichtigen Sie den weiteren Anwendungsfall des Monitors zum Drucker. Der Monitor schwarz, R=G=B=0, wird dann als nicht die höchste Dichte gedruckt. Die Auswirkung auf die Bildqualität besteht darin, dass es an Tiefe und Kontrast fehlt.

Abbildung 6: Der schwarze Punkt des Geräts ist möglicherweise dunkler als die neutrale Mindesthelligkeit.

Angenommen, das Ziel "Gerät black point" ist Jkakbk/JkCkh k. Wenn C k nicht null ist, ist der schwarze Punkt des Geräts nicht neutral relativ zu CAM02. Wenn Sie J k für das Ziel "neutrale Minimale Lichtheit" in der Konstruktion des Lichtskaler verwenden; das heißt, Einstellung

J_minOut = Jk

und wenden Sie sie auf die Quell-Gamutshell an, sie erhalten die in Abbildung 7 dargestellte Konfiguration. In der Abbildung entspricht die Farbtonebene h k.

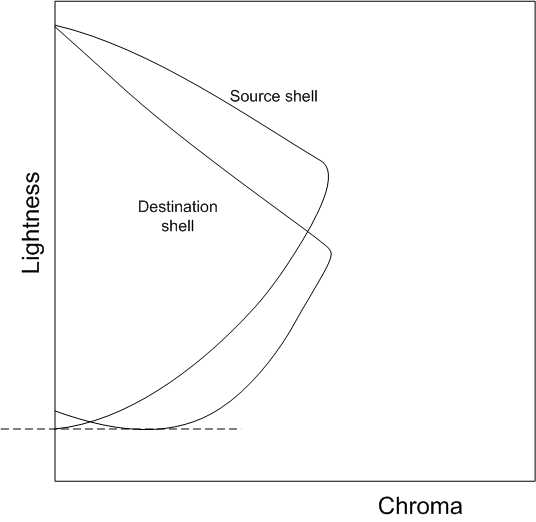
Abbildung 7: Geometrie mit dem geänderten Lichtskaler mit schwarzem Punkt des Zielgeräts

Damit der nachfolgende Farbkomprimierungsalgorithmus fortgesetzt werden kann, möchten Sie die maximalen und minimalen Lichtwerte an den Quell- und Zielschalen ausrichten. Dies kann erreicht werden, indem die Zielshell zwischen J _neutralMin und J k angepasst wird, indem die Punkte nach links verschoben werden. Darüber hinaus muss diese Transformation auf den gesamten Jab-Raum angewendet werden, nicht nur die Farbtonebene, die h k entspricht.

Die Transformation ist

Abbildung 8 zeigt den Effekt der Transformation.

Abbildung 8: Geometrie mit geänderter Lichtskala mit schwarzem Punkt des Zielgeräts

Nach dem Anwenden des üblichen Farbkomprimierungsalgorithmus muss der Punkt "zurückgesetzt" werden, d. h. die Umgekehrte Transformation muss angewendet werden, um die endgültige zugeordnete Farbe zu erhalten.

Der Fall von dualen Gamut-Shells

Ziel ist es, SIG_KNEE für einzelne Gamut-Shell auf den Fall zu generalisieren, in dem entweder das Quellgerät GBD oder das Zielgerät GBD über eine Zwei-Shell-Struktur verfügt. Die innere Shell wird als Referenzshell bezeichnet, während die äußere Shell als Plausible Shell bezeichnet wird. Sie möchten die folgenden Fälle berücksichtigen.

(a) Sowohl die QUELL-GBD- als auch die Ziel-GBD verfügen über eine Zwei-Shell-Struktur.

b) Die GBD-Quelle weist eine Zwei-Shell-Struktur auf; die Ziel-GBD verfügt nur über eine Shell.

c) Die GbD-Quelle hat nur eine Shell; das Ziel GBD verfügt über eine Zwei-Shell-Struktur.

(d) Sowohl die Quell-GBD als auch die Ziel-GBD verfügen nur über eine Shell.

Case (d) ist der Fall einer einzelnen Gamut-Shell, die zuvor erörtert wurde. Für Fälle (a), (b) und (c) können Sie die Beleuchtungsanpassung generalisieren, um die zusätzlichen Informationen aus der Dual-Shell-Struktur zu verwenden. In Fällen (b) und (c) wenn entweder die Quelle oder das Ziel nur eine Shell aufweist, führen Sie eine "induzierte Referenzshell" ein, die in einem nachfolgenden Abschnitt "Induzierte Referenzshell" behandelt wird. Der allgemeine Algorithmus für zwei Shells wird für den Fall (a) beschrieben. Nachdem die induzierte Referenzshell-Konstruktion erläutert wurde, kann der Algorithmus auch auf den Fall (b) und (c) angewendet werden. Was die Farbkomprimierung angeht, so wird das Komprimierungsverhältnis durch die größten verfügbaren Schalen bestimmt. Wenn also sowohl die Plausible Shell als auch die Referenzshell verfügbar sind, wird die Plausible Shell verwendet; andernfalls wird die Referenzshell verwendet.

Generalized Lightness Rescaling

Das Vorhandensein von zwei Shells für Quell- und Ziel-GBD bedeutet, dass Sie einen Satz von vier Punkten von der Quell-GBD zu einem entsprechenden Satz im Ziel-GBD zuordnen müssen.

Die Tiefstellen haben die folgenden Bedeutungen.

o oder r: "Original" (Quelle) oder "Reproduktion" (Ziel)

min oder max: minimale neutrale Lichtheit oder maximale neutrale Lichtheit

pla oder ref: Plausible Shell oder Referenzshell

Die Sortierung in jedem Vierfach ist auch die erwartete relative Größe dieser Punkte.

Die Lichtheits-Reskalierungszuordnung verwendet die gleichen beiden ersten Gleichungen wie die einzelne Shell, aber J S wird wie folgt in einer stückweisen Weise definiert.

(7)

Mit anderen Worten, es ist sigmoidal innerhalb der Referenzschale und linear außen. Siehe Abbildung 9.

Abbildung 9: Lichtheits-Rescaling-Funktion für zwei Shell-GBDs

INDUZIERTE REFERENZSHELL-

Wenn eine GBD über eine Shell verfügt und die andere GBD über zwei Shells verfügt, müssen Sie eine "Referenzshell" für die GBD mit nur einer Shell erstellen. Die vorhandene Shell, die als Referenzshell bezeichnet wird, wird in die "Plausible Shell" geändert. Tatsächlich müssen Sie im vollen Jab-Raum keine Shell erstellen. Da die Beleuchtungskalierung nur J max. und J minverwendet, müssen Sie diese Werte nur für die induzierte Referenzshell bilden. Je nachdem, welche GBD zwei Shells enthält, gibt es zwei Fälle.

Fall 1: Source GBD verfügt über zwei Shells; ziel GBD verfügt über eine Shell.

Bestimmen der zielinduzierten Referenzshell auf der neutralen Achse; d. h. das J _{r,\ min,\ ref} und J _{r,\ max,\ ref} der Shell. Dazu wird der folgende Algorithmus verwendet.

Die Faktoren ? _niedrige und ? _hohe die Trennung zwischen der Plausible Shell und der Referenzshell steuern. Ein Wert von 1 bedeutet, dass die J _min Werte oder J mₐₓ Werte übereinstimmen. Ihre Werte werden aus der Quellreferenzshell und der Plausible Shell "induziert".

Die "Fudge-Faktoren" F _niedrigen und F _hohen sind tunable Parameter, die zwischen 0 und 1 liegen müssen. Wenn der Wert 0 ist, werden die J _min oder J mₐₓ direkt aus den Quellschalen induziert. Wählen Sie in diesem Fall F _niedrigen = 0,95 und F _hohen = 0,1 aus.

Fall 2: Source GBD hat eine Shell; Ziel GBD verfügt über zwei Shells.

Bestimmen der quellinduzierten Referenzshell auf der neutralen Achse; d. h. das J _{o,\ min,\ ref} und J _{o,\ max,\ ref} der Shell. Dazu wird der folgende Algorithmus verwendet.

Auch hier die Faktoren? _niedrige und ? _hohe die Trennung zwischen plausible Shell und Reference Shell steuern. Ein Wert von 1 bedeutet, dass die Werte J _Min. oder J mₐₓ übereinstimmen. Ihre Werte werden aus der Quellreferenzshell und der Plausible Shell "induziert":

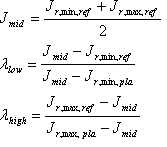
Gründe für Änderungen aus den Empfehlungen von CIE TC8-03

BasicPhoto unterscheidet sich von den Empfehlungen von CIE TC8-03 auf folgende Weise.

1. Chroma wird nicht in Richtung der Kusp komprimiert, sondern entlang der Linien der konstanten Leichtigkeit.
2. Der Lichtbereich verwendet die Hellheit der dunkelsten Farbe in der Gamut anstelle des Punkts, an dem die Gamutgrenze die neutrale Achse kreuzt.
3. BasicPhoto unterstützt sowohl eine Referenz-Gamut-Shell als auch eine plausible Gamut-Shell, wenn eine beliebige Gamutgrenze in der Transformation zwei Shells aufweist.
4. BasicPhoto verwendet CIECAM02; statt CIECAM97s zum Konvertieren in D65 bei 400 cd/m2 und dann mit RIT IPT Farbraum zu verwenden.

Die erste Änderung wurde vorgenommen, um Toninversionsprobleme zu verhindern, die bei verwendung der Komprimierung in Richtung eines Cusp auftreten können. Wie in Abbildung 10 dargestellt, kann die Cusp-Komprimierung zu Toninversionen führen. Dies kann passieren, wenn Farben mit hoher Farbfarbe heller sind als Farben von niedrigeren Chroma. Da SGCK jedes Pixel unabhängig voneinander in Leichtigkeit und Chroma komprimiert, ist es nicht garantiert, die Lichtverhältnisse zwischen den Pixelwerten nach der Komprimierung beizubehalten. Der bekannte Nachteil dieser Entscheidung, auf Linien konstanter Helligkeit zu komprimieren, besteht darin, dass Sie verluste an Chroma leiden können, insbesondere in Gebieten, in denen die Grenze für die Zielskala sehr flach ist, wie bei hellen Gelben.

Abbildung 10 : Von SGCK verursachte Toninversion

Abbildung 11 : Originalbild, SGCK-Ergebnis und BasicPhoto-Ergebnis

Abbildung 11 veranschaulicht diese Toninversion. Auf der linken Seite befindet sich ein originales Bild, das von einer Digitalkamera aufgenommen wird; in der Mitte, das Bild, wie von SGCK reproduziert; und auf der rechten Seite, das Bild, wie es von BasicPhoto reproduziert wird. Das Bild auf der linken Seite befindet sich im Farbraum der Digitalkamera, die Mitte und die rechten Bilder befinden sich im Farbraum einer LCD-Videoanzeige. Im Originalbild ist der obere Teil der Teekanne dunkler als der untere, da der untere Teil die Tischmaske widerspiegelt, auf der es sitzt. Im SGCK-Bild ist der obere Teil aufgrund der Toninversion tatsächlich heller als der untere Teil. Außerdem ist es schwierig, die Elemente im unteren Teil der Teekanne widerzuspiegeln. Auf der rechten Seite hat BasicPhoto den Ton inversion behoben, und die reflektierten Artikel sind deutlicher erkennbar.

Die zweite Änderung wurde vorgenommen, um die Reproduktion nahezu schwarzer Farben auf Druckern zu verbessern, bei denen das schwarzste Schwarz nicht direkt auf die CIECAM02 neutrale Achse fällt. Die folgende Abbildung 12 zeigt ein Bild, das in sRGB konvertiert wurde. reproduziert für einen RGB-Tintenstrahldrucker mit SGCK; und für denselben Drucker mit BasicPhoto reproduziert. Das Bild in der Mitte verwendet nicht das vollständige Gerät schwarz, daher fehlt es an dem Kontrast, der im Original zu sehen ist. Der Kontrast wird mit BasicPhoto wiederhergestellt.

Abbildung 12 : Erweitert schwarz

Die dritte Änderung wurde vorgenommen, um die Farbwiedergabe für Digitalkameras zu verbessern. Insbesondere in Fällen, in denen die Digitalkamera mit einem Referenzziel profiliert wurde, enthält eine aus gemessenen Farben gebaute Gamut-Begrenzungsbeschreibung möglicherweise nicht alle Farben, die in einer realen Szene aufgenommen werden können. Anstatt alle Farben in die Farbskala des gemessenen Farbziels zu schneiden, ermöglichen Sie die Extrapolation, um eine plausible Gamutgrenze zu erzeugen. Der BasicPhoto-Algorithmus wurde entwickelt, um eine solche extrapolierte Gamutgrenze zu unterstützen.

Die vierte Änderung wurde vorgenommen, da CIECAM02 gut für die Gamutzuordnung geeignet ist. Der von TC8-03 empfohlene Prozess der Konvertierung von Gerätefarben in D65 bei 400 cd/m2 und dann die Verwendung des RIT IPT-Farbraums ist sowohl berechnungsintensiv als auch zeitaufwändig.

Farbtonzuordnung

HueMap ist das Äquivalent der ICC-Sättigungsabsicht.

Wenn entweder die Quell-Gamutgrenze oder die Ziel-Gamut-Grenze keine Primarbereiche enthält, wird dieses Modell auf das in einem vorherigen Abschnitt beschriebene MinCD-Modell (relativ) zurückgesetzt. Beispielsweise können Geräte, für die die Primar nicht bestimmt werden können (ICC-Profile mit mehr als vier Kanälen) oder monochrome ICC-Profile.

Dieser Algorithmus passt zuerst den Farbton des Eingabefarbwerts an. Anschließend passt es gleichzeitig die Leichtigkeit und die Chroma an und verwendet dabei eine Scherungszuordnung. Schließlich wird der Farbwert ausklammert, um sicherzustellen, dass er sich innerhalb der Gamut befindet.

Der erste Schritt besteht darin, den "Hue Wheels" zu bestimmen. Suchen Sie die JCh-Werte für primäre und sekundäre Farben sowohl für das Quell- als auch für das Zielgerät. Sie berücksichtigen nur die Farbtonkomponenten. Dies führt zu einem primären oder sekundären Farbtonrad mit sechs Farbpunkten für jedes Gerät. (Siehe Abbildung 13.)

Abbildung 13 : Farbtonräder

Bessere Ergebnisse können erzielt werden, wenn die primäre Quelle blau nicht in die primäre Zielblau gedreht wird. Stattdessen wird der quellblaue primäre Farbtonwinkel als primärer Farbtonwinkel des Ziels verwendet.

Führen Sie als Nächstes die Farbtondrehungen für jede Eingabefarbe aus dem Quellbild aus,

a)Bestimmen Sie mithilfe des Farbtonwinkels der Eingabefarbe die Position der Farbe auf dem Quellfarbrad relativ zu den beiden angrenzenden Primär- oder Sekundärfarben. Die Position kann als Prozentsatz des Abstands zwischen den Primaren betrachtet werden. Beispielsweise beträgt der Eingabefarbton 40 Prozent des Weges vom Farbtonwert Magenta bis zum Farbtonwert Von Rot.

b)Suchen Sie auf dem Zieltonrad den zugehörigen Farbtonwinkel, z. B. 40 Prozent von Magenta bis Rot. Dieser Wert ist der Zieltonwinkel.

Im Allgemeinen werden die Quellprimierungen und Secondaries nicht in den gleichen Farbtonwinkeln wie die Zielprimierungen und Secondäre stehen; d. h. der Zieltonwinkel unterscheidet sich in der Regel vom Quelltonwinkel.

Angenommen, die Farbtonräder erzeugen die folgenden Werte:

Quelle M = 295 Grad, Quelle R = 355 Grad.

Ziel M = 290 Grad, Ziel R = 346 Grad.

Wenn der Farbtonwinkel der Eingabefarbe 319 Grad beträgt, beträgt er 40 Prozent des Winkels (24 Grad) von Quelle M bis Quelle R. Der Winkel von M bis R beträgt 60 Grad, und der Winkel von M bis Eingabeton beträgt 24 Grad. Berechnen Sie den Winkel auf dem Ziel, der 40 Prozent von Ziel M bis Ziel R (22 Grad) beträgt, sodass der Farbtonwinkel der Zielfarbe 312 Grad beträgt.

Berechnen Sie als Nächstes die Farbtonverweispunkte für den Quellton und den Zielton. Um den Farbtonbezugspunkt für einen bestimmten H-Wert (Farbton) zu berechnen, möchten Sie den J-Wert (Helligkeit) und den C -Wert (Chroma) ermitteln.

• Suchen Sie den J-Wert des Farbtonbezugspunkts, indem Sie zwischen den J-Werten für die angrenzenden primären oder sekundären Punkte interpolieren, indem Sie die relative Position des Farbtons verwenden; Beispiel: 40 Prozent in diesem Beispiel.
• Suchen Sie den maximalen C-Wert bei diesem J-Wert und h-Wert. Sie haben jetzt den JCh des Farbtonbezugspunkts für diesen Farbton.

Abbildung 14: Ein Farbtonblatt (Visualisierung eines Ausschnitts der Begrenzungsskala in einem bestimmten Farbton)

Der nächste Schritt besteht darin, die Scherzuordnung für jedes Pixel zu berechnen. Visualisieren Sie zunächst ein Farbtonblatt aus der Quellfarbskala für den Farbtonwinkel der Quelle und ein Farbtonblatt aus der Zielskala für den Zieltonwinkel, der während der Farbtondrehung berechnet wird. Die Farbtonblätter werden erstellt, indem ein "Segment" aus der JCh-Gamut-Begrenzungsoberfläche in einem bestimmten Farbtonwinkel verwendet wird (siehe Abbildung 14).

HINWEIS: Aus Gründen der Leistungsoptimierung werden Farbtonblätter nicht tatsächlich erstellt; sie werden nur zu Visualisierungszwecken beschrieben und hier gezeigt. Die Vorgänge werden direkt auf der Grenzfläche der Gamut am angegebenen Farbton ausgeführt. Anschließend berechnen Sie die Farbtonverweispunkte, um die Scherzuordnung zu bestimmen.

• Führen Sie eine Hellheitsänderung durch, um die schwarzweißen Punkte des Quellblatts dem Zielblatt zuzuordnen (siehe Abbildung 15). Die schwarzen und weißen Punkte des Quelltonblatts werden linear den schwarzen und weißen Punkten des Zieltonblatts zugeordnet, indem alle J-Koordinaten der Quellgrenze skaliert werden. Der Farbton-zugeordnete Eingabefarbwert wird auf die gleiche Weise skaliert.

Abbildung 15 : Lichtheitszuordnung

• Bestimmen Sie die Farbtonreferenzpunkte für jedes Farbtonblatt. Wenden Sie eine Scherzuordnung auf das Quellblatt an, sodass die Quell- und Zielbezugspunkte übereinstimmen (siehe Abbildung 16). Der Bezugspunkt für eine Gamut in einem bestimmten Farbton ist der interpolierte Farbtonbezugspunkt zwischen den angrenzenden Primaren. Der Bezugspunkt des Quelltonblatts wird linear dem Referenzpunkt des Zieltonblatts zugeordnet, wobei ein "Scher"-Vorgang verwendet wird, der die J-Achse sperrt und die schwarzen Punkte und die weißen Punkte im Mittelpunkt hält. Die schwarzen Punkte, weißen Punkte und Referenzpunkte des Quell- und Zieltons sollten übereinstimmen.
• Wenden Sie die Schubzuordnung auf den lichtbereinigten Eingabefarbwert an. Die J- und C-Koordinaten des Quellfarbwerts werden proportional skaliert, relativ zum Abstand von der J-Achse.
• Als Nächstes wird eine subtile farbabhängige Lichtkomprimierung in Richtung des J-Werts des Farbtonbezugspunkts auf dem Schub-zugeordneten Farbpunkt durchgeführt. Die Komprimierung in Richtung Farbtonbezug J erfolgt in gammaähnlicher Weise, wobei Weiß, Schwarz, Grau und Punkte auf dem Farbtonbezug J nicht betroffen sind. Alle anderen Punkte neigen zu dem Farbtonverweis J in glatter Art und Bündelung in der Nähe des Farbtonbezugs J, wobei die Farbtonkonstante noch konstant bleibt. Die Farbabhängigkeit stellt sicher, dass neutrale Farben nicht betroffen sind und der Effekt auf Farben mit höherer Farbfarbe erhöht wird.

Es folgt eine mathematische Beschreibung der Helligkeitskomprimierung in Richtung des Farbtonbezugs J oder das Anpassen des J-Werts des Zielpunkts. Er wird als Zielpunkt bezeichnet, da er in der Zielskala zugeordnet wurde.

Berechnen Sie zunächst "factorC" (Farbabhängigkeitsfaktor) für den Zielpunkt, der bestimmt, wie viel Wirkung die Lichtkomprimierung haben wird. Punkte in der Nähe oder auf der J-Achse weisen wenig oder gar keine Komprimierung auf; Von der J-Achse (High-Chroma) entfernte Punkte werden mehr Komprimierung angewendet. Multiplizieren Sie mit 0,5, um sicherzustellen, dass FaktorC kleiner als 1 ist, da es möglich ist, dass sourceC etwas größer als referenceC, aber nicht doppelt so groß sein könnte.

factorC = (destinationC / referenceC) ? 0,5

wo:

destinationC ist der C-Wert des Zielpunkts.

referenceC ist der C-Wert des Hue-Bezugspunkts.

Bestimmen Sie als Nächstes, ob der Zielpunkt J über oder unterhalb des Farbtonbezugs J liegt. Gehen Sie oben vor, gehen Sie wie folgt vor:

1. Berechnen Sie "factorJ" für den Zielpunkt relativ zum VerweisJ. Dieser FaktorJ-Wert liegt zwischen 0 und 1 (0 bei BezugJ; 1 bei maxJ).

2. factorJ = (destinationJ - referenceJ) / (maxJ - referenceJ)

   wo:

   destinationJ ist der J-Wert des Zielpunkts.

   referenceJ ist der J-Wert des Farbtonbezugspunkts.

   maxJ ist der maximale J-Wert des Gamuts.

3. Wenden Sie eine gammaähnliche Leistungsfunktion auf FactorJ an, wodurch FaktorJ um einen bestimmten Betrag reduziert wird. In diesem Beispiel wird die Potenz 2 (das Quadrat) verwendet. Subtrahieren Sie den reduzierten FaktorJ vom ursprünglichen FaktorJ, und multiplizieren Sie das Ergebnis mit dem gesamten J-Bereich oberhalb des primären BezugSJ, um das "deltaJ" zu finden, das die Änderung in J nach der Lichtkomprimierung darstellt, jedoch nicht einschließlich der Farbabhängigkeit.

4. deltaJ = (FactorJ - (FactorJ ? factorJ)) ? (maxJ - referenceJ)

5. Wenden Sie FactorC auf das DeltaJ an (je höher die Chroma, desto größer der Effekt), und berechnen Sie den neuen J-Wert für den Zielpunkt.

6. destinationJ = destinationJ - (deltaJ ? factorC)

Wenn J-Wert für den Zielpunkt unter "referenceJ" liegt, wird eine ähnliche Berechnung mit den vorherigen Schritten ausgeführt, wobei minJ anstelle von maxJ verwendet wird, um den Bereich in J zu ermitteln, um den FaktorJ zu berechnen, und unter Berücksichtigung der Polarität der Vorgänge "unter" der ReferenzJ.

factorJ = (referenceJ - destinationJ) / (referenceJ - minJ)

deltaJ = (FactorJ - (FactorJ ? factorJ)) ? (referenceJ - minJ)

destinationJ = destinationJ + (deltaJ ? factorC)

wo:

minJ ist der minimale J-Wert der Gamut.

Die Chroma für Eingabefarbpunkte wird linear (sofern möglich) entlang der konstanten Helligkeit proportional zum maximalen Farbwert der Quell- und Ziel-Gamuts in diesem Farbton und dieser Helligkeit erweitert. In Kombination mit der vorherigen farbabhängigen Lichtkomprimierung trägt dies dazu bei, die Sättigung zu erhalten, da die Scherzuordnung mit den Referenzpunkten manchmal dazu führt, dass der Quellpunkt in Chroma überkomprimieren wird (siehe Abbildung 16).

Abbildung 16 : Scherzuordnung, Lichtdichtekomprimierung in Richtung Farbtonbezug J und Farbtonerweiterung

Es folgt eine mathematische Beschreibung des Farberweiterungsprozesses oder das Anpassen des C-Werts des Zielpunkts. Es wird als Zielpunkt bezeichnet, da er in der Zielskala komprimiert und in die Zielskala komprimiert wurde.

1. Bestimmen Sie vor der Scherzuordnung "sourceExtentC" (der Farbton bei Helligkeit und Farbton des Quellpunkts).

2. Bestimmen Sie nach der Schubzuordnung und Lichtkomprimierung, die den Quellpunkt in den Zielpunkt transformiert, das destExtentC (die Farbtonausdehnung an der Helligkeit und dem Farbton des Zielpunkts).

3. Wenn die sourceExtentC größer als der destExtentC ist, ist keine Farbanpassung an den Zielpunkt erforderlich, und Sie können den nächsten Schritt überspringen.

4. Passen Sie destinationC (die Chroma des Zielpunkts) an, damit sie an dieser Helligkeit und diesem Farbton in das Ziel-Farbton passen.

5. destinationC = destinationC ? (destExtentC / sourceExtentC)

   wo:

   destinationC ist der C-Wert des Zielpunkts.

   sourceExtentC ist der maximale C-Wert der Quellskala an der Helligkeit und dem Farbton des Quellpunkts.

   destExtentC ist der maximale C-Wert der Zielskala an der Helligkeit und dem Farbton des Zielpunkts.

Führen Sie schließlich den Mimimum-Abstandsausschnitt aus. Wenn sich die farbtongedrehte, leicht angepasste Und Schub-zugeordnete Eingabefarbe noch etwas außerhalb der Zielskala befindet, schneiden Sie sie (verschieben Sie sie) an den nächstgelegenen Punkt auf der Zielskalagrenze (siehe Abbildung 17).

Abbildung 17: Abschneiden des Mindestabstands

Beschreibung der Gamut-Grenze und Gamut Shell-Algorithmen

Die Geräte-Gamut-Begrenzungsfunktion verwendet das Gerätemodellmodul und analytische Parameter, um eine Farbgeräte-Gamutgrenze abzuleiten, die als indizierte Vertexliste des Rumpfs der Geräteskala beschrieben wird. Der Rumpf wird unterschiedlich berechnet, je nachdem, ob Sie mit additiven Geräten arbeiten, z. B. Monitore und Projektoren, oder subtrahierende Geräte. Die indizierte Vertexliste wird in CIEJab gespeichert. Die Struktur der indizierten Vertexliste ist für die Hardwarebeschleunigung durch DirectX optimiert.

Dieser Ansatz hat viele bekannte Lösungen. Wenn Sie im Web nach "konvex hull DirectX" suchen, erhalten Sie mehr als 100 Treffer. Beispielsweise gibt es einen Verweis von 1983 zu diesem spezifischen Thema (Computergrafiktheorie und Anwendung, "Shiphulls, b-spline surfaces, and cadcam", S. 34-49) mit Referenzen aus dem Jahre 1970 bis 1982 zum Thema.

Die Sammlung von Punkten kann wie folgt aus extern verfügbaren Informationen bestimmt werden:

• Punkte für die Referenzshell für Monitore werden mithilfe eines Samplings des Farbwürfels im Farbraum des Geräts generiert.
• Punkte für die Referenzshell für Drucker und Aufnahmegeräte werden aus den Beispieldaten abgerufen, die zum Initialisieren des Modells verwendet werden.
• Punkte für die Referenzshell für scRGB und sRGB werden mithilfe eines Samplings des Farbwürfels für sRGB generiert.
• Punkte für die plausible Shell für Aufnahmegeräte werden mithilfe eines Samplings des Farbwürfels im Gerätefarbraum generiert.
• Punkte für die Referenzschale für Projektoren werden mithilfe eines Samplings eines Polyhedrons im Farbwürfel im Farbraum des Geräts generiert.
• Punkte für die mögliche Shell für breite Dynamische Farbräume werden mithilfe eines Samplings des Farbwürfels im Raum selbst generiert.

Sie können eine Vertexliste erstellen, die die Farbgeräteskala effizient beschreibt, sofern ein Geräteprofil und Systemsupportdienste vorhanden sind.

Bei Ausgabegeräten beschreibt die Gamutgrenze den Farbbereich, der vom Gerät angezeigt werden kann. Eine Gamut-Grenze wird aus denselben Daten generiert, die zum Modellieren des Verhaltens des Geräts verwendet werden. Konzeptionell geben Sie ein Sampling des Farbbereichs aus, den das Gerät erzeugen kann, messen sie die Farben, konvertieren die Messungen in den Darstellungsbereich und verwenden dann die Ergebnisse, um die Gamutgrenze zu erstellen.

Eingabegeräte sind komplizierter. Jedes Pixel in einem Eingabebild muss einen Wert aufweisen. Jedes Pixel muss in der Lage sein, jede Farbe in der realen Welt in irgendeiner Weise darzustellen. In diesem Sinne sind für ein Eingabegerät keine Farben "außerhalb des Gamuts", da sie immer dargestellt werden können.

Alle digitalen Bildformate weisen einen festen dynamischen Bereich auf. Aufgrund dieser Einschränkung gibt es immer einige unterschiedliche Reize, die demselben digitalen Wert entsprechen. Sie können also keine 1:1-Zuordnung zwischen realen Farben und Digitalen Kamerawerten herstellen. Stattdessen wird die Gamutgrenze gebildet, indem eine Reihe von realen Farben geschätzt wird, die die digitalen Antworten der Kamera erzeugen können. Sie verwenden diesen geschätzten Bereich als Gamut für das Eingabegerät.

Primaries sind enthalten, um die Allgemeine Kartenzuordnung für Geschäftsgrafiken bereitzustellen.

Im objektorientierten Stil abstrahieren Sie die zugrunde liegende Darstellung der Gamutgrenze. Auf diese Weise können Sie die Flexibilität haben, die Darstellung in Zukunft zu ändern. Um den im neuen CTE verwendeten Gamut-Grenzdeskriptor (GAMUT Boundary Descriptor, GBD) zu verstehen, müssen Sie zunächst verstehen, wie Gamut-Zuordnungsalgorithmen (Gamut Mapping Algorithm, GMAs) funktionieren. Traditionell wurden GVO entwickelt, um den Bedürfnissen der Grafikkunstgemeinschaft gerecht zu werden; d. h. zum Reproduzieren von Bildern, die bereits ordnungsgemäß für das Gerät gerendert wurden, auf dem das Eingabebild erstellt wurde. Ziel der GRAFIK-GVO ist es, die bestmögliche Reproduktion des Eingabebilds auf dem Ausgabegerät zu ermöglichen. Der neue CTE GBD wurde entwickelt, um vier wichtige Probleme zu lösen.

Da das Eingabebild für das Eingabegerät gerendert wird, passen alle Farben in den Bereich zwischen dem weißen Punkt des Mediums und dem schwarzen Punkt. Angenommen, das Bild ist ein Foto einer Szene, in der es ein diffuses Weiß gibt, z. B. eine Person in einem weißen Teehemd, und ein Glanzlicht, z. B. Licht, das von einem Fenster oder Chromstoßer reflektiert wird. Die Szene wird auf dem Eingabemedium gerendert, sodass die Glanzmarker dem weißen Punkt des Mediums zugeordnet wird, und das diffuse Weiß wird einer neutralen Farbe zugeordnet, die dunkler als der weiße Punkt des Mediums ist. Die Wahl der Zuordnung von Farben aus der Szene zum Eingabemedium ist sowohl eine szenenabhängige Entscheidung als auch eine ästhetische Entscheidung. Wenn die Glanzherz aus der ursprünglichen Szene fehlte, würde das diffuse Weiß wahrscheinlich dem weißen Punkt des Mediums zugeordnet werden. In einer Szene mit viel Hervorhebungsdetail würde mehr Bereich zwischen dem Glanzweiß und dem diffusen Weiß übrig bleiben. In einer Szene, in der die Hervorhebung nicht signifikant ist, bleiben möglicherweise nur sehr wenige Bereiche übrig.

Für zuvor gerenderte Bilder ist die Gamutzuordnung relativ einfach. Im Grunde wird der weiße Punkt des Originalmediums dem weißen Punkt der Reproduktion zugeordnet, der schwarze Quellpunkt wird dem schwarzen Zielpunkt zugeordnet, und die meisten der Zuordnung sind abgeschlossen. Die verschiedenen GVO bieten Variationen für die Zuordnung anderer Punkte auf der Tonskala des Quellmediums und verschiedene Möglichkeiten zur Behandlung von Out-of-Gamut-Chroma-Werten. Aber die Zuordnung von Weiß zu Weiß und Schwarz zu Schwarz ist in diesen Variationen konsistent. Diese Implementierung erfordert, dass Weiß über einem J* von 50 und schwarz unter einem J* von 50 liegt.

Nicht alle Farbcodierungen beschränken Farbbereiche für Eingabebilder. Der IEC-Standardfarbcodierungs-scRGB (IEC 61966-2-2) bietet 16 Bits für jeden der drei Farbkanäle Rot, Grün und Blau (RGB). In dieser Codierung wird bezugsschwarz nicht als RGB Triple (0, 0, 0), sondern als (4096, 4096, 4096, 4096) codiert. Bezugsweiß wird als (12288, 12288, 12288) codiert. Die scRGB-Codierung kann verwendet werden, um Glanzlichter und Schattendetails darzustellen. Es enthält RGB-Dreifache, die nicht physisch möglich sind, da sie negative Lichtmengen erfordern, und Codierungen, die sich außerhalb der CIE-Spektral locus befinden. Klar, kein Gerät kann möglicherweise alle Farben im ScRGB-Gamut erzeugen. Tatsächlich kann kein Gerät alle Farben erzeugen, die ein Mensch sehen kann. Geräte können also die ScRGB-Gamut nicht ausfüllen, und es wäre nützlich, den Teil der Gamut darzustellen, den sie ausfüllen. Jedes Gerät verfügt über einen Bereich von Werten im scRGB-Speicherplatz, den es erzeugen kann. Dies sind die "erwarteten" Farben für das Gerät; Es wäre überraschend, dass das Gerät Farben außerhalb dieser Gamut erzeugt. Es gibt eine definierte Transformation vom scRGB-Raum in den Darstellungsbereich, sodass jedes Gerät auch einen Bereich von Darstellungswerten aufweist, die erwartet werden, dass es reproduziert wird.

Sowohl scRGB als auch Eingaben von Aufnahmegeräten, die mit einem festen Ziel gekennzeichnet sind, ist es möglich, einen Wert außerhalb des Bereichs der erwarteten Werte abzurufen. Wenn jemand eine Kamera auf ein Testziel kalibriert; und erfasst dann eine Szene mit Glanzlichtern, es kann Pixel geben, die heller als der weiße Punkt des Ziels sind. Dasselbe kann passieren, wenn ein natürlich vorkommendes Rot mehr farblich ist als das Zielrot. Wenn jemand ein ScRGB-Bild von einem Gerät verwendet und dann die Farben im Bild manuell bearbeitet, ist es möglich, Pixel zu erstellen, die außerhalb des erwarteten Bereichs der Geräteskala liegen, auch wenn sie sich innerhalb der vollständigen scRGB-Gamut befinden.

Ein zweites Problem scheint zunächst nicht damit verbunden zu sein. Es tritt auf, wenn Sie ein Farbziel verwenden, um ein Eingabegerät zu charakterisieren, z. B. eine Kamera oder ein Scanner. Reflektierende Ziele werden in der Regel auf Papier produziert und enthalten eine Reihe farbiger Patches. Manufaturer stellen Datendateien mit Farbmessungen bereit, die unter einem festen Anzeigezustand für jeden Farbpatch durchgeführt werden. Farbprofilerstellungstools erstellen eine Zuordnung zwischen diesen Messwerten und den Werten, die von den Farbsensoren auf den Geräten zurückgegeben werden. Das Problem besteht darin, dass diese Farbziele häufig nicht den gesamten Bereich der Gerätewerte abdecken. Beispielsweise kann der Scanner oder die Kamera einen Wert von (253, 253, 253) für den weißen Bezugspunkt zurückgeben, und ein roter Bezugspatch kann einen RGB-Wert (254, 12, 4) aufweisen. Diese stellen den Bereich der erwarteten Werte für das Eingabegerät basierend auf den Zielwerten dar. Wenn Sie das Eingabegerät basierend auf den Antworten auf das Ziel charakterisieren, erwarten Sie nur Farben innerhalb dieses schmalen Bereichs. Dieser Bereich ist nicht nur kleiner als der Farbbereich, den Menschen sehen können, es ist kleiner als der Bereich der Farben, die das Gerät erzeugen kann.

In beiden Fällen ist es schwierig, die Gamut des Eingabegeräts oder Bilds trotz des Vorhandenseins einer Referenzskala oder Messungen zu schätzen. Im ersten Problem ist die plausible Gamut des Eingabegeräts kleiner als die vollständige Gamut von scRGB. Im zweiten Problem ist die Referenzskala des Ziels kleiner als die vollständige mögliche Gamut des Eingabegeräts.

Das dritte Problem betrifft die Tonzuordnung. Es wurden viele Modelle von Gamutgrenzen vorgeschlagen, die in den Grafikgrafiken eingesetzte vorrenderte Bilder angemessen darstellen können, z. B. die Braun- und Fairchild Mountain Range GBD (Braun[97]) und Morovics Segment Maxima Grenzdeskriptor (Morovic[98]). Diese Modelle liefern jedoch nur Informationen über die Extreme der Geräteskala; Sie fehlen Informationen zu anderen Punkten in der tonalen Zuordnung. Ohne solche Informationen können GVO nur grobe Schätzungen der optimalen Tonzuordnung vornehmen. Schlimmer noch, diese Modelle bieten keine Hilfe für den erweiterten Dynamischen Bereich in scRGB und in Digitalkamerabildern.

Wie ist dieses Problem in der foto- und videografischen Industrie gelöst? Die Kamera erfasst ein Bild. Experten könnten diskutieren, wie viel Rendering auf dem Aufnahmegerät auftritt; aber sie stimmen zu, dass es kein erheblicher Betrag ist. Beide Technologien ordnen in einer aufgenommenen Szene kein diffuses Weiß dem weißen Punkt des Mediums zu. Ebenso ordnen sie den schwarzen Punkt von der Szene zum schwarzen Punkt des Mediums nicht zu. Das Verhalten des fotografischen Films wird im Dichteraum mithilfe einer charakteristischen Kurve beschrieben, die oft als Hurter und Driffield bezeichnet wird, oder H&D-Kurve. Die Kurve zeigt die Dichte der originalen Szene und die resultierende Dichte auf dem Film. Abbildung 18 zeigt eine typische H-&D-Kurve. Die x-Achse stellt eine zunehmende Protokollbelichtung dar. Die Y-Achse stellt die Dichte auf der Folie dar. Fünf Bezugspunkte sind auf der Kurve markiert: Schwarz ohne Detail, das die Mindestdichte auf dem Negativen darstellt; schwarz mit Detail; Referenz mittelgraue Karte; weiß mit Detail; und weiß ohne Details. Beachten Sie, dass zwischen Schwarz ohne Detail (das Gerät schwarz darstellt) und Schwarz mit Detail (Schatten schwarz) vorhanden ist. Ebenso gibt es Leerraum zwischen Weiß mit Detail (diffuses Weiß) und Weiß ohne Details (was Gerät weiß darstellt).

Abbildung 18 : H&D-Kurve für Folienfilm

Die Videoindustrie bietet "Kopfraum" und "Fußraum" in Bildern. In der ITU 709-Spezifikation wird die Leuchtdichte (Y) in 8 Bits mit einem Bereich von 0 bis 255 codiert. Verweis schwarz ist jedoch mit 15 codiert, und Bezugsweiß wird als 235 codiert. Dadurch bleibt der Codierungsbereich zwischen 236 und 255, um Glanzlichter darzustellen.

Die Videoindustrie präsentiert ein im Wesentlichen geschlossenes Loop-System. Während es viele verschiedene Geräteanbieter gibt, basieren Videosysteme auf Referenzgeräten. Es gibt eine Standardcodierung für Videobilder. Es ist nicht erforderlich, eine Gamutgrenze mit Videobildern zu kommunizieren, da alle Bilder für die Vervielfältigung auf demselben Referenzgerät codiert sind. Film ist auch geschlossene Schleife, da zwischen verschiedenen Komponenten keine Zwischendaten vermittelt werden müssen. Sie möchten eine Lösung, die Bilder von Geräten mit unterschiedlichen Gamuts ermöglicht und sowohl gerenderte als auch nicht gerenderte Szenen für die Ausgabe mit unterschiedlichen Gamuts reproduziert.

Ein viertes Problem, das das neue CTE beheben muss, besteht darin, dass die visuell grauen Farben, die von einem Gerät erzeugt werden, z. B. wenn rot=grün=blau auf einem Monitor, häufig nicht auf die neutrale Achse der CAM fallen (wenn die Chroma = 0,0). Dies führt zu großen Schwierigkeiten für GVO. Damit GMAs gut funktionieren, müssen Sie die Beschreibung der Gamut des Geräts und der Eingabepunkte anpassen, damit die neutrale Achse des Geräts auf die neutrale Achse des Geräts fällt. Sie müssen Punkte von der neutralen Achse um einen ähnlichen Betrag anpassen. Andernfalls können Sie keine gleichmäßigen Abstufungen durch das Bild vornehmen. Auf dem Weg aus dem GMA können Sie diese Zuordnung relativ zur neutralen Achse des Ausgabegeräts rückgängig machen. Dies wird als "chiropractische" Begradigung der Achse bezeichnet. Wie ein Chiropractor begradigen Sie nicht nur das Skelett (neutrale Achse), sondern passen den Rest des Körpers so an, dass er sich mit dem Skelett bewegt. Wie ein Chiropractor passen Sie das Skelett nicht um dieselbe Menge durch den gesamten Raum an. Stattdessen passen Sie unterschiedliche Abschnitte unterschiedlich an.

Abbildung 19: Krümmung der neutralen Achse des Geräts relativ zur CIECAM-Neutralachse

Das neue CTE erfordert ein Modell einer Gamut-Grenze, die verwendet werden kann, um sowohl gerenderte als auch nicht gerenderte Quellbilder darzustellen, Informationen über das Erscheinungsbild von Geräteneutralen bereitzustellen und Informationen für Tonabbildungsbilder mit einem breiten Leuchtdichtebereich bereitzustellen.

Abbildung 20 : Drei Gamut-Shells

Die Gamutgrenze besteht aus drei Shells, die drei Bereiche definieren.

Im neuen CTE wird die äußere Hülle des Gamuts mit einem konvexen Rumpf gebildet, der aus Beispielpunkten im Gerätespektrum hergestellt wird. Ein Rumpf wird durch eine Reihe von Beispielpunkten gebildet und sie durch eine Oberfläche umgeben. Ein konvexer Rumpf hat die zusätzliche Eigenschaft, überall konvex zu sein. Daher ist dies nicht der kleinste mögliche Rumpf, der an die Daten angepasst werden kann. Aber Experimenten haben gezeigt, dass das Anpassen der Beispielpunkte zu eng verursacht unappealierende Artefakte in Bildern, z. B. ein Mangel an glatter Schattierung. Der konvexe Rumpf scheint diese Probleme zu lösen.

Im Algorithmus werden Farbdarstellungswerte für eine Reihe von Punkten abgerufen, die vom Gerät abgefragt werden. Bei Monitoren und Druckern werden die Farbdarstellungswerte durch Ausgabebeispiele abgerufen und anschließend gemessen. Sie können auch ein Gerätemodell erstellen und dann synthetische Daten über das Gerätemodell ausführen, um Messwerte vorherzusagen. Die Gemessenen Werte werden dann aus dem farbmetrischen Raum (XYZ) in den Darstellungsraum (Jab) konvertiert, und der Rumpf wird um die Punkte umschlossen.

Der Wichtigste für diesen Algorithmus ist, dass der angenommene weiße Punkt, der bei der Konvertierung von colorimetrisch in den Darstellungsbereich verwendet wird, nicht der weiße Punkt des Mediums sein muss. Stattdessen können Sie einen Punkt weiter innerhalb der Gamut und auf (oder in der Nähe) der neutralen Achse auswählen. Dieser Punkt hat dann den J-Wert 100. Proben mit einem gemessenen Y-Wert, der höher als der angenommene Weiße Punkt ist, enden mit einem J-Wert, der größer als 100 ist.

Wenn Sie den diffusen weißen Punkt der Szene als angenommenen Weißen Punkt für die Farbraumkonvertierung platzieren, werden glanzförmige Hervorhebungen in der Szene leicht erkannt, da ein J-Wert größer als 100 ist.

Da das CIECAM02 Farbmodell auf dem menschlichen visuellen System basiert, wird die Leuchtdichte des schwarzen Punkts (J = 0) automatisch durch das Modell bestimmt. Wenn das Eingabebild einen breiten dynamischen Bereich aufweist, kann es vorkommen, dass Werte vorhanden sind, die J-Werten kleiner als 0 entsprechen.

In der folgenden Abbildung 21 sind die Geräteneutrale dargestellt, die in der Mitte der Plausiblen und Referenz gamuts ausgeführt werden.

Abbildung 21: Geräteneutrale Achse zur Gamutgrenze hinzugefügt

Alle Gamutzuordnungen umfassen entweder das Ausschneiden eines Eingabebereichs auf eine Ausgabeskala oder das Komprimieren der Eingabeskala, um in die Ausgabeskala einzupassen. Komplexere Algorithmen werden durch Komprimieren und Abschneiden in unterschiedlichen Richtungen oder durch Dividieren der Gamut in verschiedene Bereiche gebildet und dann clipping oder Komprimierung in den verschiedenen Bereichen durchgeführt.

Das neue CTE erweitert dieses Konzept, um die Regionen einer möglichen Gamut, einer plausiblen Gamut und einer Referenzskala zu unterstützen, und ermöglicht es GVO, sie auf unterschiedliche Weise zuzuordnen. Darüber hinaus verfügen die GVO über Informationen über die geräteneutrale Achse. In der folgenden Diskussion wird erläutert, wie Situationen behandelt werden, in denen die plausiblen Gamuts und Referenz gamuts aufeinander reduziert sind.

Abbildung 22 : GMA mit zwei nicht reduzierten Gamutdeskriptoren

Dieses Beispiel wird möglicherweise angezeigt, wenn Sie von einem Eingabegerät, z. B. einer Kamera oder einem Scanner, die mit einem reflektierenden Ziel gekennzeichnet sind, dem ScRGB-Raum zuordnen. Hier sind die plausiblen Farben, die heller als Bezugsweiß sind Glanzlichter. In der Praxis generiert die Charakterisierung einer Kamera mit einem Ziel möglicherweise nicht den vollständigen Wertebereich, der in der Kamera möglich ist; Glanzlichter und sehr farbliche Farben, die in der Natur zu finden sind, würden jedoch in der Natur vorkommen. (Transmissive Ziele haben in der Regel einen Patch, der die minimale Dichte auf dem Medium möglich ist. Bei einem solchen Ziel würden glanzförmige Hervorhebungen innerhalb des Zielbereichs liegen.) Der Bezug schwarz für ein reflektierendes Ziel wäre der Anfang des schattenschwarzen Bereichs. Das heißt, es gibt wahrscheinlich Farben in den Schatten, die dunkler als das Schwarz auf dem Ziel sind. Wenn das Bild viele interessante Inhalte in dieser Region enthält, kann es sinnvoll sein, diese tonale Variation beizubehalten.

Abbildung 23: GMA mit reduzierter Zielskala

In Abbildung 23 ist ein möglicher Gamutzuordnungsalgorithmus dargestellt, wenn die Zielskala nur den Bereich von Gerät Weiß bis Schwarz bereitstellt, und es gibt keine möglichen Farben außerhalb dieser Gamut. Dies geschieht wahrscheinlich für typische Ausgabegeräte, z. B. Drucker. Die möglichen Farben werden dem Rand der Zielskala zugeordnet. Es fehlt jedoch eine Tonkurve für das Ausgabegerät. Das GMA muss einen neutralen Punkt mit niedrigerer Leuchtdichte auswählen, um als Zuordnungsziel für das Referenzweiß zu verwenden. Ein anspruchsvoller Algorithmus kann dies tun, indem die Lichtheiten im Quellbild histogrammiert werden und sehen, wie viele in den erwarteten, aber helleren Bereich fallen als der Bezugsweiß. Je mehr Leichtigkeit erforderlich ist, desto mehr Platz ist im Zielgerät zwischen den zugeordneten Punkten für die Glanzlichter und bezugsweiß erforderlich. Ein einfacherer Algorithmus kann einen beliebigen Abstand zur Lichtskala von Gerät weiß auswählen, z. B. 5 Prozent. Ein ähnlicher Ansatz gilt für die Zuordnung der maximalen Schwarzen und Schattenschwarzen.

Nachdem Sie die Zieltonkurve generiert haben, können Sie eine Methode zuordnen, die in der vorherigen Abbildung 23 verwendet wird. Alle Punkte in der Zieltonkurve fallen in die Geräteskala, und alle Punkte in der Zuordnung müssen in die Geräteskala fallen.

Wenn Sie die linken Abbildungen und die rechten Abbildungen und die Richtungen der Pfeile in Abbildung 23 umkehren, können Sie den Fall beschreiben, in dem das Quellbild nur einen Bezugsskala aufweist, und die drei Gamuts des Ausgabegeräts sind nicht miteinander reduziert. Ein Beispiel hierfür kann eine Zuordnung von einem Monitor zu scRGB sein. Auch hier muss das GMA die Kontrollpunkte für die fünf Punkte der Tonkurve für das Quellbild synthetisieren. Einige Zuordnungen platzieren möglicherweise alle Punkte der Tonkurve innerhalb der ScRGB-Geräteskala, während andere Zuordnungen möglicherweise mehr scRGB-Gamut verwenden, indem diffuses Weiß dem Referenzweiß zugeordnet und Glanzweiß einem helleren Wert zugeordnet werden kann.

Schließlich haben Sie den Fall, dass beide Geräte nur über die Referenzskala verfügen. Dies ist die Funktionsweise der meisten Gamutzuordnungsalgorithmen. So können Sie dies beheben, indem Sie einfach auf aktuelle Algorithmen zurückfallen. Wenn Sie auch eine vernünftige Möglichkeit haben, die fünf Referenzpunkte für die Quell- und Zielgeräte zu bestimmen, können Sie die Referenzpunkte zuordnen.

Geräte gamuts enthalten mehr als die fünf Referenzpunkte auf der neutralen Achse. Diese stellen nur die Grenzen zwischen potenziellen Regionen im Bild dar. Zwischen jedem der Referenzpunkte können Sie eine der vorhandenen Gamut-Zuordnungstechniken verwenden. Sie können also den Bereich unerwarteter Farben abschneiden und alle Farben zwischen dem erwarteten Weißen und Schwarz komprimieren, oder Sie können alle Farben außerhalb des Referenzbereichs abschneiden und innerhalb dieses Bereichs komprimieren. Es gibt viele Möglichkeiten, die in verschiedenen GVO implementiert werden können. Darüber hinaus können die GVO auf unterschiedliche Weise komprimieren und abschneiden. Alle diese Kombinationen sind in dieser Erfindung abgedeckt.

Bisher wurde in dieser Diskussion die Gamut behandelt, als ob es sich nur um eine Funktion des Geräts handelte, auf dem das Bild erstellt, erfasst oder angezeigt wurde. Es gibt jedoch keinen Grund, warum alle Bilder für ein Gerät dieselbe Gamut aufweisen müssen. Die GVO hängen von den Daten im GBD ab. Wenn der Deskriptor zwischen Bildern geändert wird, gibt es keine Möglichkeit für die GVO zu wissen. Wenn Bilder keine glanzförmigen Hervorhebungen aufweisen, sind GVO besser geeignet, wenn der Gamutdeskriptor nicht anzeigt, dass Farben heller als diffuses Weiß sind.

In der neuen CTE-Architektur ist es möglich, mehr als ein GMA zu verwenden. Die Verwendung mehrerer GVO ist inhärent schlecht definiert. Wenn ein Aufnahmegerät z. B. einem GMA sein "Aussehen und Verhalten" zuordnet, wird dies in der Regel mit einer "gezielten" Zielskala ausgeführt. Das gleiche gilt für Ausgabegeräte und "gezielte" Quell gamuts. Die sRGB-Gamut ist eine häufig implizierte Gamut. Daher wird dringend empfohlen, ein einzelnes GMA zu verwenden, wenn die Vorhersagbarkeit eine Priorität ist. Ein einzelner GMA-Workflow sollte die Standardeinstellung für alle Workflows sein, insbesondere für Consumer- und Prosumer-Workflows. Während die Gamutzuordnung für die bevorzugte Reproduktion einmal erfolgen sollte, gibt es Instanzen, in denen mehrere Zuordnungsprozesse enthalten sind. Zuerst führen Sie für die Korrekturhilfe eine bevorzugte Zuordnung zur Gamut des endgültigen Zielgeräts und dann ein farbmetrisches Rendering zur Gamut des Korrekturhilfegeräts durch. Zweitens werden einige Arten von Zuordnungen verwendet, um die Merkmale des Bilds zu ändern, sind jedoch nicht enthalten, um einer Geräteskala zuzuordnen, z. B. die Anpassung der Tonkurve oder die Farbigkeit. Wenn mehrere GMAs verwendet werden, verwendet die Transformationsschnittstelle ein Array gebundener Gamutzuordnungen, d. h. Gamut-Karten, die mit einem Paar von Gamut-Begrenzungsbeschreibungen initialisiert wurden. Wenn mehr als eine Gamutzuordnung vorhanden ist, muss die Eingabeskalagrenze für eine erfolgreiche Gamutzuordnung mit der Ausgangs-Gamutgrenze des Vorgängers identisch sein.

Die Geräte-Gamut-Begrenzungsfunktion verwendet das Gerätemodellmodul und analytische Parameter und leitet eine Farbkörper-Gamutgrenze ab, die als sortierte Vertexliste des Konvex-Rumpfs der Geräteskala beschrieben wird. Die sortierte Vertexliste wird in CIEJab gespeichert. Die Struktur der sortierten Vertexliste ist für die Hardwarebeschleunigung durch DirectX optimiert. Dieser Ansatz hat viele bekannte Lösungen (suchen Sie im Web nach "convex hull DirectX", und Sie erhalten gut 100 Treffer). Es gibt auch einen Verweis von 1983 zu diesem Thema (Computergrafiktheorie und Anwendung, "Shiphulls, b-spline oberflächen and cadcam" S. 34-49), mit Referenzen aus dem Jahre 1970 bis 1982 zum Thema.

Zwei verschiedene Techniken können verwendet werden, um die Dreiecke in der Gamut-Shell zu berechnen. Für andere Geräte als additive RGB-Geräte berechnen Sie einen konvexen Rumpf. Sie können die Untersuchung von Nichtkonvex-Rumpfunterstützung für andere Geräte in Betracht ziehen, wenn Sie direkten Zugriff auf solche Geräte haben, um die Stabilität, Leistung und Genauigkeit der Algorithmen zu überprüfen. Dies ist ein bekannter Prozess, der keine weitere Beschreibung erfordert. Die für additive RGB-Geräte verwendete Technik wird wie folgt beschrieben.

Verschiedene GBDs haben Vorteile und Nachteile. Die konvexe Rumpfdarstellung garantiert schöne geometrische Eigenschaften, z. B. konvexe Farbtonsegmente, die einen einzigartigen Schnittpunkt mit einem Raymaning von einem Punkt auf der neutralen Achse bieten. Der Nachteil der konvexen Rumpfdarstellung ist auch Konvexität. Es ist bekannt, dass viele Geräte, insbesondere Anzeigegeräte, Gamuts haben, die weit davon entfernt sind, konvex zu sein. Wenn die tatsächliche Gamut erheblich von der Konvexitätsannahme abweicht, wäre die Konvex-Rumpfdarstellung ungenau, möglicherweise in dem Maße, in dem sie die Realität nicht darstellt.

Nachdem Sie eine GBD angenommen haben, die eine relativ genaue Darstellung des tatsächlichen Gamuts gibt, treten andere Probleme auf, einige aufgrund des Konzepts des Farbtonsegments. Es gibt mindestens zwei pathologische Situationen. In der folgenden Abbildung 24 ergibt ein CRT-Gamut Farbtonsegmente mit "Inseln". In Abbildung 25 führt eine Druckerskala zu einem Farbtonsegment, bei dem ein Teil der neutralen Achse fehlt. Die pathologischen Farbtonsegmente werden in diesen Fällen nicht durch besonders pathologische Gamutgrenzen verursacht. Sie werden durch das Konzept des Farbtonsegments verursacht, da (a) es entlang des konstanten Farbtons genommen wird, und (b) es dauert nur eine Hälfte der Ebene, die dem Farbtonwinkel entspricht.

Abbildung 24: Ein typischer CRT-Monitor weist eine Gamut auf, die in den blauen Farbtonen eigenartige "Curving in" zeigt. Wenn Farbtonsegmente innerhalb dieses Farbtonbereichs aufgenommen werden, können isolierte Inseln in den Farbtonsegmenten angezeigt werden.

Abbildung 25: Ein Drucker weist möglicherweise eine Lücke auf der neutralen Achse auf. Wenn ein Farbtonsegment genommen wird (das nur eine Hälfte der Ebene ist), gibt es einen "Dent" auf dem Teil der Grenze, die die neutrale Achse ist. Dies kann schwierig sein, algorithmisch aufzulösen.

Um diese Pathologien zu lösen, wird ein neues Framework vorgeschlagen, das das Konzept des Farbtonsegments aufgibt, das als Ausgangspunkt verwendet wird. Stattdessen verwendet das Framework den Satz von "Begrenzungslinienelementen" oder Linien, die sich auf der Gamutgrenze befinden. Sie bieten nicht unbedingt eine kohärente geometrische Visualisierung wie Farbtonsegmente, aber sie unterstützen alle gängigen Gamut-Vorgänge. Neben der Lösung der zuvor erwähnten Probleme schlägt dieser Ansatz auch vor, dass die Konstruktion von Farbtonsegmenten, auch wenn es möglich ist, rechenschwenderisch ist.

Triangulation der Gamut-Grenze

Der Ausgangspunkt ist eine GBD, die aus einer Triangulation der Gamutgrenze besteht. Bekannte Methoden zum Erstellen von GBDs stellen in der Regel diese Triangulation bereit. Für Betonung wird hier eine Methode zum Erstellen von GBDs für additive Geräte beschrieben. Zu diesen Geräten gehören Monitore (CRT-basiert und LCD-basiert) und Projektoren. Mit der einfachen Geometrie des Würfels können Sie ein normales Gitter auf dem Würfel einführen. Die Begrenzungsflächen des Würfels können in einer Reihe von Arten trianguliert werden, z. B. die in Abbildung 26 dargestellte. Die Architektur stellt entweder ein Gerätemodell für das Gerät bereit, sodass farbmetrische Werte der Gitterpunkte algorithmisch abgerufen werden können, oder Messungen wurden direkt für diese Punkte vorgenommen. Die Architektur bietet auch CIECAM02, sodass Sie davon ausgehen können, dass die Startdaten bereits CIECAM02 Jab-Raum zugeordnet wurden. Anschließend weist jeder Gitterpunkt auf den Begrenzungsflächen des RGB-Cubes einen entsprechenden Punkt im Jab-Raum auf. Die Verbindungen von Punkten, die den Satz von Dreiecken im RGB-Raum bilden, löst auch eine Reihe von Dreiecken im Jab-Raum aus. Diese Dreiecke bilden eine vernünftige Triangulation der Gamutgrenze, wenn (a) das Gitter auf dem RGB-Würfel fein genug ist, und (b) die Transformation von Geräteraum in den einheitlichen Farbraum ist toplogisch gut verhalten; d. h., sie ordnet grenzende Grenze zu, und sie dreht den Gamut nicht innen, sodass innere Punkte zu Grenzpunkten werden.

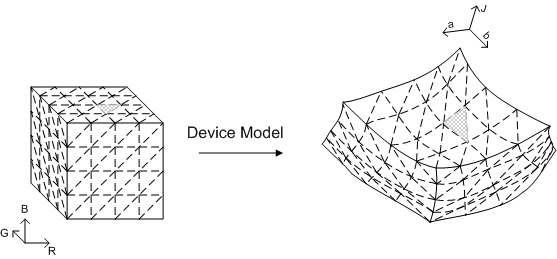
Abbildung 26: Eine einfache Methode zum Triangulieren der Gamutgrenze eines Geräts mit RGB als Geräteraum

Begrenzungslinienelemente

Zentraler Bestandteil dieses Rahmens ist das Konzept von Grenzlinienelementen; eine Reihe von Liniensegmenten, die (a) auf der Gamutgrenze liegen und (b) auf einer Ebene liegen. In diesem Fall ist die Ebene eine Farbtonebene. Jedes Liniensegment ist das Ergebnis, dass die Ebene mit einem Grenzdreieck überschneiden wird. Obwohl viele Forscher die Konstruktion einer Ebene mit Grenzdreiecken verwendet haben, analysieren sie im Allgemeinen die Beziehung zwischen diesen Liniensegmenten und versuchen, ein kohärentes geometrisches Objekt aus den Liniensegmenten zu konstruieren. Verschiedene Algorithmen wurden entwickelt, um diese Liniensegmente nacheinander zu verfolgen, bis ein ganzes Farbtonsegment abgerufen wird, und es wurden viele Versuche unternommen, den Suchvorgang zu beschleunigen.

Dieser Ansatz unterscheidet sich. Sie schneiden die Ebene mit den Dreiecken, um die Liniensegmente zu erhalten. Sie betrachten diese Liniensegmente dann als die grundlegenden konzeptionellen Objekte. Es ist notwendig, die Beziehung zwischen den Liniensegmenten zu analysieren; Sie müssen nicht wissen, wie sie miteinander verbunden sind. Dieser Standpunkt löst das Problem des Farbtonsegments mit Inseln. Die bekannten Ansätze, die versuchen, Farbtonsegment zu konstruieren, gehen davon aus, dass, wenn man mit einem Liniensegment beginnt und es zum nächsten Liniensegment folgt usw.; es führt schließlich zurück zum Ausgangspunkt, an dem ein ganzes Farbtonsegment konstruiert werden würde. Leider würde dieser Ansatz die Insel (und im schlimmsten Szenario, den Kontinent) verpassen. Indem sie nicht darauf bestehen, ein kohärentes geometrisches Bild zu erhalten; Das heißt, Farbtonsegment, Sie können das Inselproblem mühelos behandeln. Ein weiterer wichtiger Unterschied bei diesem Ansatz besteht darin, dass zum Beschleunigen der Konstruktion von Liniensegmenten ein "Dreiecksfilter" verwendet wird. Der Dreiecksfilter löst bestimmte Dreiecke aus, die definitiv keine Liniensegmente erzeugen, die im aktuellen Gamut-Vorgang nützlich wären. Da das Überschneiden eines Dreiecks mit der Ebene teuer ist, verbessert dies die Geschwindigkeit. Ein Nebeneffekt ist, dass Sie farbtonsegment nicht erstellen können, da einige Liniensegmente aufgrund der Dreiecksfilterung fehlen würden.

Gamut-Vorgang: CheckGamut

Im folgenden Beispiel wird erläutert, wie das Framework funktioniert und wie CheckGamut durchgeführt wird, d. h. der Vorgang der Überprüfung, ob eine Farbe im Gamut ist.

Das allgemeine Framework ist in der folgenden Abbildung 27 dargestellt. Es gibt verschiedene Komponenten. Die in Kursiv bezeichneten Komponenten sind Komponenten, die je nach betreffenden Gamut-Vorgang unterschiedlich sein können. Die anderen Komponenten sind in allen Gamut-Vorgängen invariant. Zunächst ist die Eingabe- eine Reihe von Farbattributen. Bei CheckGamut handelt es sich um die Abfragefarbe. In Abbildung 27 und der folgenden Diskussion wird davon ausgegangen, dass der Farbtonwinkel entweder zu den Eingabefarbattributen gehört oder aus ihnen abgerufen werden kann. Dies ist eindeutig der Fall, wenn es sich bei der Eingabe um den gesamten Farbpunkt handelt, entweder in Jab oder JCh, aus dem Sie dann den Farbtonwinkel berechnen können. Beachten Sie, dass der Farbtonwinkel nur benötigt wird, weil Farbtonebenen verwendet werden. Je nach betreffenden Gamut-Betrieb ist es möglicherweise nicht erforderlich, die Farbtonebene zu verwenden. Beispielsweise sollten Sie bei der Konstruktion des Routine-CheckGamut-Steuerelements Ebenen von Konstante J verwenden. Dies ist eine Allgemeinheit, die nicht weiter verwendet oder erörtert wird; aber es kann hilfreich sein, sich an diese Flexibilität der Methodik zu erinnern, um andere Gamut-Operationen zu unterstützen, wenn Farbtonebene möglicherweise nicht die beste Wahl ist.

Abbildung 27: Das Framework zur Unterstützung von Gamutvorgängen

Der Farbtonwinkel, der direkt aus den Eingaben abgerufen oder aus den Eingaben berechnet wird, wird verwendet, um die Farbtonebene zu initialisieren, die Full Hue Plane in der Abbildung bezeichnet wird. "Full" wird betont, weil dies die volle Ebene ist, nicht nur die halbe Ebene, die den Farbton enthält. Die volle Ebene enthält sowohl den Eingabetonwinkel als auch den Winkel um 180 Grad gegenüber. Die schlüsselfunktion der Farbtonebene ist die Intersect-Funktion, die im folgenden Unterabschnitt erläutert wird, Full Hue Plane: Intersect. Gehen Sie davon aus, dass die GBD bereits erstellt wurde und die Gruppe der Gamut Boundary Triangles verfügbar ist. Schneiden Sie die Dreiecke, die den Dreiecksfilter überstanden haben, mit der Farbtonebene überschneiden. Der Dreiecksfilter Komponente ist kursiv beschriftet, was bedeutet, dass die Komponente bei verschiedenen Gamut-Vorgängen unterschiedlich ist. Der Dreiecksfilter für CheckGamut wird im Abschnitt"Gamut Operation: CheckGamut (fortsetzung) erläutert. Das Ergebnis der Übersecting eines Dreiecks mit der Farbtonebene ist entweder leer oder ein Boundary Line Element , d. h. ein Paar unterschiedlicher Punkte. Wenn das Ergebnis nicht leer ist, wird es an den Line Element Processor übergeben, was je nach Gamut-Vorgang wiederum unterschiedliche Aktionen ausführt. Der Line Element Processor aktualisiert die interne Datenstruktur, internen verarbeiteten Daten, deren Inhalt oder Layout ebenfalls vom Gamutvorgang abhängt. Im Allgemeinen enthält die interne verarbeitete Daten die "Antwort" auf das Problem, das ständig mit jedem neuen Begrenzungslinienelement aktualisiert wird. Wenn alle Begrenzungslinienelemente verarbeitet wurden, wurde die Antwort gefunden. Sie bleibt über die Output Adaptordarauf zugreifen. Da die internen verarbeiteten Daten spezifisch ist, ist der Ausgabeadapter auch gamut-operationspezifisch.

Volle Farbtonebene: Überschneiden

Die Intersect-Funktion berechnet den Schnittpunkt der Farbtonebene und eines Dreiecks. So einfach es klingt, ist diese Funktion aus zwei Gründen wichtig.

Erstens kann die Überschneidung der einzelnen Dreiecksränder mit der Ebene drei Schnittpunkte ergeben, eine geometrisch unmögliche Situation. Der Grund, warum dies bei der Berechnung passieren kann, besteht darin, dass bei Berechnungen im Gleitkommaformat, z. B. IEEE-Format, Unsicherheiten oder "numerisches Rauschen" in jedem Schritt vorhanden sind, der die Schlussfolgerung beeinflusst, ob ein Rand die Ebene überschneidet. Wenn die Ebene die Kanten in einer Nahfehlsituation überschneidet, befinden sich die Schnittpunkte nahe beieinander, und die Bestimmung, ob ein Schnittpunkt innerhalb des Rands liegt, ist zufällig. Obwohl Rauschen in den numerischen Werten der Punkte klein ist, ist die qualitative Schlussfolgerung, dass es mehr als zwei Schnittpunkte gibt, geometrisch unmöglich und schwer im Algorithmus zu behandeln.

Zweitens befindet sich diese Funktion in der kritischen Schleife für jeden Rand jedes gefilterten Dreiecks, daher ist es wichtig, dass Sie seine Effizienz so weit wie möglich optimieren.

Führen Sie die Berechnungen in ganzzahligen Zahlen aus, um das erste Problem mit numerischem Rauschen zu beheben. Um das zweite Problem der Optimierung der Effizienz zu beheben, zwischenspeichern Sie das am häufigsten verwendete Attribut jedes Scheitelpunkts oder das "Dot-Produkt", das jedem Scheitelpunkt zugeordnet ist. Das Übergeben in ganze Zahlen ist eine typische Methode, um geometrische Konsistenz zu gewährleisten. Die Grundidee lautet: Wenn Sie quantisieren müssen, tun Sie dies am Anfang. Dann können nachfolgende Berechnungen in ganzzahligen Zahlen durchgeführt werden, und wenn die ganzen Zahlen breit genug sind, damit keine Überlaufgefahr besteht, können die Berechnungen mit unendlicher Genauigkeit durchgeführt werden. Die folgende Quantisierungsfunktion ist für diesen Zweck nützlich.

ScaleAndTruncate(x) = Ganzzahliger Teil von x*10000

Der Skalierungsfaktor 10000 bedeutet, dass die Gleitkommazahl der Eingabe vier Dezimalstellen aufweist, was für diese Anwendung genau genug ist. Je nach Wertebereich des Farbdarstellungsbereichs möchten Sie einen ganzzahligen Typ mit Bits auswählen, die breit genug sind, um die Zwischenberechnungen zu halten. In den meisten Farbdarstellungsräumen liegt der Bereich jeder Koordinate innerhalb des Bereichs -1.000 bis 1.000. Die quantisierte Koordinate hat einen maximalen absoluten Wert von 1.000*10.000 = 10.000.000. Wie Sie sehen, ist die Zwischenmenge ein Punktprodukt, bei dem es sich um eine Summe von zwei Koordinatenprodukten handelt, sodass ein maximal möglicher Absoluter Wert von 2*(10.000.000) ?10 ₁₄ aufweist. Die Anzahl der erforderlichen Bits ist log ₄ ) = 47,51. Eine bequeme Wahl für den ganzzahligen Typ ist daher 64-Bit-Ganzzahlen.

Um sicherzustellen, dass die Überschneidung einer Ebene mit einem Dreieck immer einen leeren Satz oder eine Reihe von zwei Punkten angibt, müssen Sie das Dreieck als Ganzes betrachten, nicht als einzelne Ränder des Dreiecks separat. Um die geometrische Situation zu verstehen, berücksichtigen Sie die "signierten Entfernungen" der Scheitelpunkte des Dreiecks von der Farbtonebene. Berechnen Sie diese signierten Entfernungen nicht direkt; Berechnen Sie stattdessen die Punkteprodukte der Positionsvektoren der Scheitelpunkte mit dem quantisierten Normalvektor auf die Ebene. Genauer gesagt, während der Initialisierung der Farbtonebene wird der quantisierte Normalvektor wie folgt berechnet.

NormalVector = (ScaleAndTruncate(-sin(hue)), ScaleAndTruncate(cos(hue)))

Beachten Sie, dass dieser Vektor ein zweidimensionaler Vektor ist. Sie können einen zweidimensionalen Vektor verwenden, da die Farbtonebene vertikal ist, sodass die dritte Komponente des normalen Vektors immer null ist. Darüber hinaus wird eine Nachschlagetabelle mit Punktprodukten initialisiert, um einen Eintrag für jeden Scheitelpunkt aus den Dreiecken der Gamut-Grenze und das entsprechende Punktprodukt auf einen ungültigen Wert festzulegen.

Bei einem Vorgang, bei dem die Farbtonebene mit einem Dreieck durchsucht wird, wird das Punktprodukt jedes Scheitelpunkts des Dreiecks nachschlagen. Wenn der Wert in der Nachschlagetabelle der ungültige Wert ist, wird das Punktprodukt mithilfe des folgenden Ausdrucks berechnet.

NormalVector.a*ScaleAndTruncate(vertex.a) + NormalVector.b*ScaleAndTruncate(vertex.b)

Auch hier wird die J-Komponente des Scheitelpunkts nie verwendet, da der normale Vektor horizontal ist. Dieses Punktprodukt wird dann in der Nachschlagetabelle gespeichert, sodass es nicht erneut berechnet werden muss, wenn das Punktprodukt des Scheitelpunkts später abgefragt wird.

Zwischenspeichern ermöglicht eine schnelle Bestimmung, ob ein Rand die Ebene überschneidet, nachdem die Punkteprodukte in der Nachschlagetabelle tabuliert wurden, die schrittweise erstellt wird, während die Scheitelpunkte verarbeitet werden.

Abbildung 28: Überschneiden der Farbtonebene mit einem Dreieck

Damit das Dreieck in Abbildung 28 die Farbtonebene in einem nicht degenerierten Liniensegment überschneidet, müssen sich die Punkteprodukte der Scheitelpunkte in einer der folgenden Muster befinden, wenn sie in aufsteigender Reihenfolge sortiert sind.

0,0,+; -,0,0; -,0,+; -,-,+; -,+,+

Ein Endpunkt des Liniensegments entsteht, wenn die Fläche durch einen Rand mit Scheitelpunkten mit unterschiedlichen Schildern im Punktprodukt überschneiden wird. Wenn das Zeichen null ist, liegt der Scheitelpunkt direkt auf der Ebene, und der Schnittpunkt des Rands mit der Ebene ist der Scheitelpunkt selbst. Beachten Sie auch, dass die Fälle 0,0,0; -,-,0; 0,+,+ werden nicht gemeldet. Der erste Fall (0,0,0) bedeutet, dass das gesamte Dreieck auf der Ebene liegt. Dies wird nicht gemeldet, da jeder Rand des Dreiecks zu einem benachbarten Dreieck gehören sollte, das nicht auch vollständig auf der Ebene liegt. Der Rand wird gemeldet, wenn dieses Dreieck berücksichtigt wird. Die anderen beiden Fälle (-,-,0 und 0,+,+) entsprechen der geometrischen Konfiguration, die das Dreieck in einem Scheitelpunkt berührt. Diese Fälle werden nicht gemeldet, da sie nicht zu einem nicht entgenerten Liniensegment führen.

Der vorangehende Algorithmus bestimmt, wann eine Schnittmenge zwischen einem Rand des Dreiecks und der Farbtonebene berechnet wird. Nachdem ein Rand bestimmt wurde, wird die Schnittmenge mit parametrischen Formeln berechnet. Wenn eines der Punkteprodukte null ist, ist die Schnittmenge der Scheitelpunkt selbst, sodass keine Berechnung erforderlich ist. Wenn beide Punkteprodukte der Scheitelpunkte des Rands ungleich Null sind, ist Vertex1 der Scheitelpunkt mit negativen Punktprodukt dotProduct1; und Vertex2 ist der Scheitelpunkt mit positiven Punktprodukt dotProduct2. Diese Reihenfolge ist wichtig, um sicherzustellen, dass der berechnete Schnittpunkt nicht davon abhängt, wie die Reihenfolge der Scheitelpunkte in der Darstellung des Rands angezeigt wird. Das geometrische Konzept des Rands ist symmetrisch in Bezug auf seine Scheitelpunkte. Der rechentechnische Aspekt der Verwendung parametrischer Gleichungen des Rands führt zur Asymmetrie (Auswahl des Anfangsvertex), was aufgrund numerischer Rauschen und Konditionierungen der zu lösenden linearen Gleichungen einen etwas anderen Schnittpunkt geben kann. Mit diesem Hinweis wird der Schnittpunkt, Schnittpunkt, durch folgendes angegeben.

t = dotProduct1/(dotProduct1 - dotProduct2)

Schnittpunkt. J = Scheitelpunkt1. J + t * (Vertex2. J - Scheitelpunkt1. J)

intersection.a = vertex1.a + t * (vertex2.a - vertex1.a)

intersection.b = vertex1.b + t * (vertex2.b - vertex1.b)

Gamut Operation: CheckGamut (fortsetzung)

Der grundlegende geometrische Algorithmus, der für die Gamutüberprüfung verwendet wird, besteht darin, die Anzahl der Strahlenübergänge zu zählen. Berücksichtigen Sie für einen bestimmten Abfragepunkt einen Strahl, der mit dem Abfragepunkt beginnt und nach oben zeigt (J-Richtung). Zählen Sie, wie oft dieser Strahl die Gamutgrenze überschreitet. Wenn diese Zahl gerade ist, ist der Abfragepunkt außerhalb des Gamuts. Wenn diese Zahl ungerade ist, befindet sich der Punkt innerhalb. Grundsätzlich kann dieser Algorithmus in 3D implementiert werden, es wird in der Regel durch Schwierigkeiten durch degenerierte Situationen, wie z. B. das Strahlendreieck (teilweise) auf einem Grenzdreieck oder die niederdimensionale Degeneracie, wie z. B. der Strahl, der (teilweise) an einem Rand eines Grenzdreiecks liegt (teilweise) plagen, geplagt. Selbst in 2D müssen Sie mit diesen entgenerten Situationen umgehen; aber das Problem ist einfacher und wurde auf zufriedenstellende Weise behoben. Siehe [O'Rourke].

Bestimmen Sie für einen bestimmten Eingabepunkt Jab den Farbtonwinkel h wie folgt.

h = atan(b/a),

Initialisieren Sie die Farbtonebene, und bestimmen Sie dann die Begrenzungslinienelemente, die dieser Farbtonebene entsprechen. Da die Begrenzungslinienelemente nur relevant sind, wenn sie den Aufwärtsstrahl überschneiden, richten Sie einen Dreiecksfilter ein, um Dreiecke zu entfernen, die Linienelemente enthalten, die den Aufwärtsstrahl definitiv nicht schneiden. Betrachten Sie in diesem Fall das umgebende Feld des Dreiecks. Der Aufwärtsstrahl überschneidet das Dreieck nicht, wenn sich der Abfragepunkt außerhalb des "Schattens" befindet, der durch das umgebende Feld gegossen wird, wenn sich eine Lichtquelle direkt darüber befand. Aufblasen Sie dies leicht mit einer vordefinierten Toleranz, um numerisches Rauschen zu ermöglichen, sodass Sie nicht versehentlich Dreiecke wegwerfen, die nützliche Linienelemente enthalten können. Das Ergebnis ist der halb unendliche rechteckige Zylinder in Abbildung 29. Prüfen, ob sich der Abfragepunkt innerhalb oder außerhalb dieses Zylinders befindet, kann mithilfe einfacher Ungleichheiten effizient implementiert werden.

Abbildung 29 : Dreiecksfilter für CheckGamut

CheckGamut verfügt über drei spezifische Komponenten für den Gamut-Betrieb: Interne verarbeitete Daten,Line Element Processorund Output Adaptor. Die internen verarbeiteten Daten ist eine Liste von Zeilenelementen, die von Line Element Processorverarbeitet wurden. In diesem Fall fügt der Line Element Processor der Liste einfach ein Linienelement hinzu. Die interne Datenstruktur für Interne verarbeitete Daten kann entweder eine verknüpfte Liste oder ein Array sein, das größer werden kann.

Der Ausgabeadapter ist ein Modul, das auf die Liste der Linienelemente zugreift, bestimmt, ob ein Linienelement den Aufwärtsstrahl kreuzt (Anzahl 1) oder nicht (Anzahl 0). Das Addieren aller dieser Zählungen gibt eine Gesamtanzahl an. Der Ausgabeadapter gibt letztendlich eine Antwort von "Ja" (gamut) oder "nein" (out-of-gamut) aus, je nachdem, ob die Gesamtanzahl ungerade oder sogar ist. Der Schritt, in dem Sie bestimmen, ob ein Linienelement den Aufwärtsstrahl kreuzt, verdient eine gewisse Aufmerksamkeit, da hier das Problem der Degeneracie auftritt und auch das Problem der Überzählung entsteht. Nach [O'Rourke] muss sich der rechte Endpunkt (der Endpunkt mit größerem Farbstoff) genau auf der rechten Seite des Strahls befinden, damit ein Linienelement den Strahl überschreitet. Dies garantiert, dass, wenn ein Endpunkt jemals genau auf dem Strahl liegt, nur einmal gezählt wird. Die gleiche Regel löst auch die degenerate Situation, in der das Linienelement genau auf dem Strahl liegt. Sie erhöhen nicht die Anzahl für dieses Linienelement.

Abbildung 30 zeigt die resultierenden Linienelemente einer Beispielskala mit dem Abfragepunkt an verschiedenen Positionen.

Abbildung 30 : Funktionsweise von CheckGamut

Minimale Farbdifferenz-Gamutzuordnung

Die Mindestfarbdifferenz-Gamutzuordnung, MinDEMap, weist eine einfache Spezifikation auf: Wenn eine Farbe im Gamut ist, tun Sie nichts. Wenn eine Farbe außerhalb des Gamuts liegt, projizieren Sie sie auf den "nächstgelegenen" Punkt auf der Gamutgrenze. Das Schlüsselwort "nearest" ist erst gut definiert, wenn Sie angeben, welche Farbdifferenzgleichung verwendet werden soll. Um die Berechnung zu vereinfachen und schneller zu machen, wird der euklidean Abstand des gewählten Farbdarstellungsbereichs oder einer Variante davon als Farbdifferenzmetrik verwendet. Der Vorteil der Euklidischen Metrik besteht darin, dass sie mit dem Punktprodukt des Raums kompatibel ist, was es ermöglicht, lineare Algebra zu verwenden. Im Detail, wenn ein "Punktprodukt" im Raum definiert ist, kann ein Abstand als Quadratwurzel des Punktprodukts des Differenzvektors mit sich selbst definiert werden. Ein Punktprodukt kann in der Regel durch eine positive 3x3 Matrix A definiert werden.

u?v = u _T Av

wobei die rechte Seite die übliche Matrixmultiplikation ist. Wenn A die Identitätsmatrix ist, wird das Standardmäßige Punktprodukt wiederhergestellt. Wenn Jab der Farbraum ist, sollten Sie die Komponenten nicht mischen, sodass eine andere diagonale Matrix als die Identitätsmatrix verwendet werden kann. Darüber hinaus können Sie die Skalierung auf einem und b unverändert halten, damit das Maß des Farbtons erhalten bleibt. Daher ist eine nützliche Variante des Euklidischen Punktprodukts die folgenden.

w _J (J-Komponente von Ihnen)(J-Komponente von v) + (eine Komponente von Ihnen)(eine Komponente von v) + (b Komponente von Ihnen)(b Komponente von v)

wobei w _J eine positive Zahl ist. Eine weitere Variante besteht darin, w _J mit dem Eingabeabfragepunkt variieren zu lassen:

w _{J\ =} w _J (queryPoint)

Das Endergebnis ist ein Maß für den Abstand, der in Bezug auf die beiden Punkte asymmetrisch ist, und mit unterschiedlichen relativen Gewichten bei Leichtigkeit und Farbton, da der Eingabeabfragepunkt variiert. Dies entspricht einigen Beobachtungen über die menschliche Farbwahrnehmung, dass Farbunterschiede in allen Dimensionen nicht gleichmäßig gewichtet werden. Es wurde festgestellt, dass Menschen weniger empfindlich für Unterschiede in der Leichtigkeit sind, als es sich um Unterschiede in Farbton und Farbton handelt.

Die folgende Gewichtungsfunktion ist nützlich.

w _J = k ₁ (C - C mₐₓ ) n

wobei k ₓ = 1, k ₁ = 0,75/(C mₐₓ ) n, C mₐₓ = 100, n = 2 und C ist der kleinere Farbfarb des Abfragepunkts und C mₐₓ.

so dass ein Gewicht von 0,25 auf den J-Begriff gesetzt wird, wenn Chroma null ist, und ein Gewicht von 1, wenn Chroma 100 ist. Der Trend, weniger Gewicht auf J zu legen, wenn Chroma klein ist, und mehr Gewicht auf J, wenn Chroma groß ist, folgt der empfohlenen Verwendung für CMC und CIEDE2000.

Abbildung 31: Die Gewichtungsfunktion der J-Komponente der Metrik

Verwenden Sie Jab-Leerzeichen für das folgende Beispiel. Es ist rechenintensiv, alle Grenzdreiecke zu durchsuchen, um den nächstgelegenen Punkt in der Euklidischen Metrik zu bestimmen. Es folgt ein einfacher Ansatz, um diesen Prozess so effizient wie möglich zu gestalten, ohne zusätzliche Annahmen einzuführen, die den Prozess beschleunigen können, sondern auch nur in einer ungefähren Antwort enden. Zunächst ist es notwendig, die geometrische Prozedur des Projizierens eines Punkts auf das angegebene Dreieck zu verstehen. Hier wird eine Beschreibung angegeben.

Eine orthogonale Projektion auf die unendliche Ebene, die das Dreieck enthält, wird zuerst durchgeführt. Der kürzeste Abstand des Abfragepunkts von der Ebene kann in zwei Schritten bestimmt werden.

(a) Berechnen des Einheitsnormalvektors auf das Dreieck.

(b) Berechnen des Punktprodukts des Einheitsnormalvektors und eines aus dem Abfragepunkt gebildeten Vektors und eines Punkts auf dem Dreieck; das heißt, einer seiner Scheitelpunkte. Da der normale Vektor eine Einheitslänge aufweist, ist der absolute Wert dieses Punktprodukts der Abstand des Abfragepunkts von der Ebene.

Der projizierte Punkt ist möglicherweise nicht die Antwort, da er außerhalb des Dreiecks liegen könnte. Sie müssen also zuerst eine Prüfung durchführen. Die Berechnung entspricht der Berechnung der baryzentrischen Koordinaten des projizierten Punkts relativ zum Dreieck. Wenn sich der projizierte Punkt innerhalb des Dreiecks befindet, ist dies die Antwort. Wenn nicht, wird der nächstgelegene Punkt an einem der Ränder des Dreiecks erworben. Führen Sie eine Suche an den drei Rändern aus. Das Bestimmen der Projektion des Abfragepunkts auf einem Rand ist ein Prozess, der der Projektion auf das Dreieck ähnelt, aber einer Dimension weniger. Eine orthogonale Projektion wird zuerst berechnet. Wenn der projizierte Punkt am Rand liegt, ist dies die Antwort. Wenn nicht, wird der nächstgelegene Punkt auf einem der beiden Endpunkte erworben. Führen Sie eine Suche auf den beiden Endpunkten durch; Das heißt, berechnen Sie den Abstand des Abfragepunkts von jedem, und vergleichen Sie, welcher kleiner ist.

Sorgfältige Untersuchung zeigt, dass es eine Menge wiederholter Suche gibt, wenn Sie durch alle Dreiecke gehen, da ein Rand immer von zwei Dreiecken geteilt wird, und ein Scheitelpunkt, der von mindestens drei Kanten geteilt wird. Darüber hinaus sind Sie nicht viel daran interessiert, den nächstgelegenen Punkt zu einem bestimmten Dreieck zu finden; Stattdessen sind Sie daran interessiert, den nächstgelegenen Punkt zur gesamten Gamutgrenze zu finden. Ein bestimmtes Dreieck wäre jedoch das, in dem dies erreicht wird. Es gibt zwei Strategien, mit denen Sie die Suche beschleunigen können.

Strategie. Jeder Scheitelpunkt wird höchstens einmal verarbeitet. Jeder Rand wird höchstens einmal verarbeitet.

Strategie II. An jedem Punkt in der Suche haben Sie einen besten Kandidaten mit der entsprechenden besten Entfernung. Wenn Sie anhand einer Schnellüberprüfung feststellen können, dass ein Dreieck nicht in der Lage ist, einen besseren Abstand zu schaffen, müssen Sie die Berechnung nicht weiter fortsetzen. Sie benötigen für dieses Dreieck nicht den nächstgelegenen Punkt und abstand.

Abbildung 32 : Minimale DE-Zuordnungsschematik

Abbildung 32 zeigt den allgemeinen Logikfluss für die Gamutzuordnung MinDEMap. Für einen Abfragepunkt wird die CheckGamut-Funktion zuerst aufgerufen. Wenn sich der Punkt im Gamut befindet, ist die Karte ein no-op. Wenn der Punkt außerhalb des Gamuts liegt, rufen Sie ProjectPointToBoundary auf. Fahren Sie nun mit Abbildung 33 fort. An diesem Punkt wird davon ausgegangen, dass die folgenden Werte berechnet wurden.

(a) Einheitsnormalvektor zu jedem Gamut-Grenzdreieck im Hinblick auf das Standard-Punktprodukt.

(b) Vertexliste und Randliste zusätzlich zur Dreiecksliste.

Abbildung 33: Die ProjectPointToBoundary-Routine

All dies sind ein konstanter Aufwand und würden die Kosten verringern, wenn ausreichende Abfragen zu dieser Gamutgrenze vorgenommen werden. In der Regel ist dies der Fall, wenn Sie eine Transformationslut von einem Gerät in ein anderes erstellen, wobei nur zwei feste Gamuts vorhanden sind, und die Transformationsverdünnung durch Punkte im einheitlich stichprobenförmigen Raster verläuft. Sie berechnen die normalen Vektoren im Hinblick auf das Standard-Punktprodukt, auch wenn der Begriff der Senkrechtheit auf dem gewichteten Punktprodukt basiert, das von dem Abfragepunkt abhängt, wie zuvor erläutert. Der Grund ist, dass ein normaler Vektor im Hinblick auf das gewichtete Punktprodukt leicht aus dem normalen Vektor in Bezug auf das Standard-Punktprodukt abgerufen werden kann. Wenn n ₀ ein normaler Vektor im Hinblick auf das Standardpunktprodukt ist, dann

n = (J-Komponente von n ₀ /w _J, a-Komponente von n ₀, b-Komponente von n ₀ )

ist normal für das Dreieck im Hinblick auf das gewichtete Punktprodukt. Aufgrund dieser Beziehung ist es immer noch vorteilhaft, n ₀ vorab zu berechnen, obwohl sie basierend auf dem Abfragepunkt angepasst werden muss.

Die ProjectPointToBoundary-Routine beginnt mit dem Zurücksetzen des "verarbeiteten Verlaufs" der Scheitelpunkte und Kanten. Dies sind Tabellen mit BOOLEAN-Flags, die nachverfolgen, ob zuvor ein Scheitelpunkt oder ein Rand besucht wurde. Außerdem wird die Variable ShortestDistance auf "INFINITY" zurückgesetzt. Dabei handelt es sich um den maximal codierten Wert im verwendeten Gleitkommazahlensystem. Dann wird sie durch eine Schleife ausgeführt und sucht anhand des ProcessTriangle-Aufrufs nach dem nächstgelegenen Punkt aus jedem Dreieck. ProcessTriangle ist die Routine zum Aktualisieren der ShortestDistance-Variablen und ist eindeutig in der kritischen Schleife. Eine Optimierung besteht darin, zu stoppen, wenn das Ergebnis gut genug ist. Nach jedem Aufruf von ProcessTriangle wird die Variable ShortestDistance untersucht. Wenn er einem vordefinierten Schwellenwert entspricht, können Sie den Wert beenden. Der vordefinierte Schwellenwert hängt vom verwendeten Farbraum und der erforderlichen Genauigkeit des Farbbildsystems ab. Bei einer typischen Anwendung möchten Sie nicht unnötig arbeiten, wenn der Farbunterschied kleiner ist als das, was von der menschlichen Sicht erkannt werden kann. Bei CIECAM02 beträgt dieser Farbunterschied 1. Verwenden Sie in der Implementierung jedoch einen Schwellenwert von 0,005, um die Genauigkeit der Berechnungen beizubehalten, da dies möglicherweise nur ein Zwischenschritt in einer Kette von Transformationen ist.

ProcessTriangle implementiert die vorangehende Strategie II. Durch Abrufen eines normalen Vektors vom vorrechenten Einheitsnormalvektor zum Dreieck im Hinblick auf das Standard-Punktprodukt berechnet es den Abstand des Abfragepunkts zur unendlichen Ebene, die das Dreieck enthält, indem das Punktprodukt des Einheitsnormalvektors und der QueryVector, der Vektor aus einem der Scheitelpunkte des Dreiecks, gebildet wird, vertex1, to the query point, queryPoint.

queryVector = queryPoint - vertex1

Abstand = | normalVector * queryVector |/||normalVector||

Dies ist eine relativ kostengünstige Berechnung, und der Abstand ist erforderlich, um weitere Berechnungen durchzuführen. Wenn diese Entfernung nicht kleiner ist als die aktuelle beste Entfernung, ShortestDistance, erzeugt dieses Dreieck keine bessere Entfernung, da es keine bessere Entfernung als die ebene, die sie enthält. In diesem Fall geben Sie die Steuerung zur Dreiecksschleife zurück. Wenn der Abstand kleiner als "ShortestDistance" ist, haben Sie möglicherweise einen näheren Punkt, wenn dieser Punkt innerhalb des Dreiecks liegt. Sie müssen einige "harte" Berechnungen durchführen (obwohl nichts über lineare Algebra hinausgeht), um dies zu bestimmen. Wenn die anderen beiden Scheitelpunkte des Dreiecks Scheitelpunkt2 und Vertex3 sind, bilden Sie die Basisvektoren firstBasisVector und secondBasisVector.

firstBasisVector = vertex2 - vertex1

secondBasisVector = vertex3 - vertex1

Verwenden Sie das folgende lineare Formelsystem, um Unbekannte zu lösen.

firstBasisVector * queryVector = (firstBasisVector * firstBasisVector)u + (firstBasisVector * secondBasisVector)v

secondBasisVector * queryVector = (secondBasisVector * firstBasisVector)u + (secondBasisVector * secondBasisVector)v

und die Bedingungen für den projizierten Punkt, der innerhalb des Dreiecks liegen soll, sind:

0 ≤ u ≤ 1, 0 ≤ v ≤ 1 und Sie + v ≤ 1

Wenn nach dieser Berechnung festgestellt wird, dass der projizierte Punkt innerhalb des Dreiecks liegt, haben Sie einen neuen nächstgelegenen Punkt gefunden. Der Abstand, den Sie am Anfang berechnet haben, ist die neue kürzeste Entfernung. Aktualisieren Sie in diesem Fall die Variablen ShortestDistance und ClosestPoint. Wenn der projizierte Punkt außerhalb des Dreiecks liegt, finden Sie möglicherweise einen näheren Punkt an einem seiner Ränder. Sie können also die ProcessEdge-Routine auf jedem der drei Kanten aufrufen.

Abbildung 34 : ProcessEdge- und ProcessVertex-Routinen

Die ProcessEdge-Routine implementiert Strategie I, die in Abbildung 34 veranschaulicht wird. ProcessEdge beginnt mit der Überprüfung, ob der Rand zuvor verarbeitet wurde. Wenn ja, wird keine weitere Maßnahme ergriffen. Wenn nicht, wird die orthogonale Projektion des Abfragepunkts auf die unendliche Linie berechnet, die den Rand enthält. Die lineare Algebra, die an der Berechnung beteiligt ist, ähnelt den vorherigen Dreiecksgleichungen. Die Berechnung ist jedoch einfacher, sie wird hier nicht beschrieben. Wenn sich der projizierte Punkt innerhalb des Rands befindet, finden Sie den Abstand des projizierten Punkts vom Abfragepunkt. Wenn diese Entfernung kleiner als "ShortestDistance" ist, haben Sie einen neuen nächstgelegenen Punkt gefunden. Aktualisieren Sie sowohl ShortestDistance als auch ClosestPoint. Wenn sich der projizierte Punkt außerhalb des Rands befindet, rufen Sie "ProcessVertex" auf den beiden Endpunkten auf. Aktualisieren Sie vor dem Zurückgeben des Steuerelements den Edgeverlauf so, dass dieser Rand als "VERARBEITET" gekennzeichnet ist.

Schließlich geben Sie eine Beschreibung von ProcessVertex. Die ProjectVertex-Routine implementiert außerdem Strategie I und verwaltet eine Vertexverlaufstabelle. Wie in Abbildung 34 dargestellt, prüft sie zunächst, ob der Scheitelpunkt zuvor verarbeitet wurde. Wenn ja, wird keine weitere Maßnahme ergriffen. Andernfalls wird der Abstand des Scheitelpunkts vom Abfragepunkt berechnet. Wenn der Abstand kleiner als ShortestDistance ist, aktualisieren Sie sowohl ShortestDistance als auch ClosestPoint. Am Ende aktualisiert sie den Vertexverlauf so, dass dieser Scheitelpunkt als "VERARBEITET" markiert ist.

Wenn die äußere Kontrollschleife entweder alle Dreiecke ausgeschöpft oder beendet wurde, bevor der Schwellenwert für den Farbunterschied erreicht wurde, wird auf die Variable ClosestPoint zugegriffen. Dies ist das Ergebnis von MinDEMap. Der Aufrufer kann auch ShortestDistance abrufen, wenn Sie daran interessiert sind, wie weit die zugeordnete Farbe von der Abfragefarbe stammt.

Farbtonglättung

Abbildung 35 : Farbtonglättung

Ein Problem tritt bei Vorgängen auf, die farbtongeschränkt sind; d. h., der Vorgang berücksichtigt nur Variablen innerhalb einer Farbtonebene. Abbildung 35 zeigt ein Beispiel für eine Gamut mit "nicht zusammenhängenden" Farbtonsegmenten in den Blauen Farbtönen. Innerhalb dieses Farbtonbereichs ist die Gamutgrenze für bestimmte Farbtonwinkel tangential für die Farbtonebene. Dies bewirkt eine Änderung der topologischen Struktur der Farbtonsegmente. Im gezeigten Beispiel ergibt sich eine "Insel", wie die Farbtonebene über diesen Farbtonbereich reißt und untertaucht. Diese Änderung in der Topologie führt dazu, dass farbtonspezifische Vorgänge nicht zusammenhängend sind. Beispielsweise ändert sich der Cusp bei festem Farbton abrupt, wenn sich der Farbtonwinkel in diesem Bereich ändert.

Es gibt einen Farbwissenschaftsgrund, warum es wünschenswert ist, farbton in bestimmten Vorgängen zu erhalten. Um das vorherige Problem zu beheben, müssen die ursprünglichen Gamut-Grenzdreiecke "farbtonglättet" sein. Im Allgemeinen ist eine Farbtonglättung einer Reihe von Gamut-Begrenzungsdreiecken eine Reihe von Dreiecken, sodass (a) sie die Grenze einer neuen "Gamut" bildet, die möglicherweise nicht der tatsächlichen Geräteskala entspricht und die die durch die ursprüngliche Gruppe von Dreiecken definierte Gamut enthält; und (b) die Dreiecke im neuen Satz werden davon abgegrenzt, parallel zu den Farbtonebenen zu sein.

Eine praktische Möglichkeit, einen farbtonglätteten Satz von Dreiecken zu erhalten, besteht darin, den konvexen Rumpf der ursprünglichen Scheitelpunkte zu nehmen. Wie in Abbildung 35 dargestellt, variieren die Farbtonsegmente des konvexen Rumpfes reibungslos im problematischen Farbtonbereich, ohne plötzliche Änderung der Topologie.

Festlegen von Primaren und Secondaries in der Beschreibung der Gamut-Grenze

Bestimmte Gamut-Zuordnungsmethoden, z. B. HueMap, hängen vom Standort der Geräteprimierungen und Secondärdateien ab. Bei additiven Geräten sind die Primar rot, grün und blau (R, G und B); und die Secondaries sind Zyan, Magenta und Gelb (C, M und Y). Bei subtrahtiven Geräten sind die Primarstellen C, M und Y; und die Secondaries sind R, G und B. Die GBD verfolgt alle sechs dieser Werte sowie weiß und schwarz (W und K) in einem Array von Jab-Farbwerten. Diese Werte werden bei der Erstellung in die Beschreibung der Gamutgrenze festgelegt. Bei Ausgabegeräten können die Primarwerte durch Ausführen von Kombinationen von Gerätesteuerungswerten über das Gerätemodell bestimmt werden. Bei Aufnahmegeräten eignet sich dieser Ansatz nicht gut zum Erstellen des Referenz-GBD, da es fast unmöglich ist, ein Bild zu erfassen, das einen vollständig gesättigten reinen Gerätewert wie (0,0, 0,0, 1,0) liefert. WCS-Geräteprofile enthalten die Indizes der Primarwerte im Aufnahmeziel. Da diese Werte nicht in einem ICC-Profil enthalten sind, verwenden Sie Werte, die von einem typischen Scannerziel gemessen wurden, nachdem sie in Jab konvertiert wurden, relativ zu den ICC-Anzeigebedingungen.

Festlegen der neutralen Achse in der Beschreibung der Gamut-Grenze

Die HueMap- und die Relative MinCD-Gamutzuordnungsmethoden verwenden die Geräteneutralachse für die Begradigung. Für die Basisausgabegeräte kann die neutrale Achse durch Ausführen von geräteneutralen Werten (R=B oder C=M=Y) über die DeviceToColorimetric-Methode und dann über die ColorimetricToAppearance-Methode des CIECAM02-Objekts bestimmt werden. Aufnahmegeräte geben jedoch nicht immer einen neutralen Wert zurück, wenn ein neutrales Beispiel angezeigt wird. Dies gilt insbesondere, wenn die Umgebungsbeleuchtung nicht perfekt neutral ist. WCS-Geräteprofile enthalten die Indizes der neutralen Proben im Ziel. Verwenden Sie diese Beispiele, um die neutrale Achse festzulegen. Da diese Informationen für ICC-Profile nicht verfügbar sind, müssen Sie dieselbe Methode verwenden, die für Ausgabegeräte verwendet wird; Führen Sie geräteneutrale Beispiele über die DeviceToColorimetric-Methode aus, und koppeln Sie dann die Eingabewerte und die farbmetrischen Ergebnisse.

Verwandte Themen

Grundlegende Farbverwaltungskonzepte

Windows-Farbsystemschemas und Algorithmen