Understanding and adapting to data drift
Drift broadly refers to changes in data and the concepts and mechanisms that they represent over time. It is common to see drift divided into two categories:
- Data drift: Data drift occurs when there is a change in input distribution that may (real drift) or may not (virtual drift) affect the class boundaries.
- Model drift: Model drift (real drift) occurs when an actual change in the class boundary occurs.
It's important to understand that model drift does not occur if there is no data drift. Both need to be detected, and both require adaptation. For this reason, "drift" can be thought of as a single phenomenon that impacts both data and models.
Drift occurs when something legitimate changes about the data generating process. A relatable example of drift is a user's preference evolution on a video streaming app. For example, a user might be interested in teen dramas during their teenage years, but gradually become more interested in documentaries. These types of changes should trigger an adaptation in recommender models. Adaptation in this example allows the streaming service's recommender system to remain relevant by suggesting progressively fewer teen dramas, and progressively more documentaries. So, the major benefit of drift detection is informing model adaptation. So, obviously, all deployed models require some form of model management and maintenance. Drift detection makes model management possible in an empirically supported and informed manner.
Drift needs to be detected early in the data pipeline and before any data reaches the learning system. If a data validation problem is identified, it should immediately stop the flow of poor-quality data and take steps to rectify the issue. Validated data should continue to flow though.
Drift vs. data validation
Now that we have a concept of what drift is (see above), let's focus on what drift is not. Drift detection and data validation are commonly mistaken as being one and the same. However, they have different implications and mitigation methods. Data validation issues are caused by illegitimate changes in the data generating process. Examples include:
- A data pipeline issue causing a feature to no longer be populated or to be populated differently – perhaps where NAN values were expected, there are now values of –1.
- Feature value ranges may be outside of reasonable expectations – blood pressure readings report a value outside of humanly possible ranges.
- Changes in schema or feature drift.
Whereas drift detection is as discussed above.
Real-world impact
The greatest benefit of drift detection is that it informs model adaptation. Most enterprise scenarios have some sort of temporal component, and thus require adaptation and maintenance. Drift detection informs the system about when a drift has occurred and about drift characteristics like magnitude and duration. This information is then used to adapt the learning system appropriately. Instead of following a fixed retrain schedule (that may not align with the actual drift) and adapt to the current concept effectively, adaptive solutions:
- Ensure that models remain accurate and representative through time
- Reduce manual analysis during model update
- Increase the longevity of solutions
- Provide insights as to why a change has occurred that may have otherwise been overlooked
Characterizing drift
Different drifts can vary wildly in terms of their characteristics. Below we discuss several relevant categories of drift characteristics.
Virtual vs real
As mentioned in the above discussion of data drift vs. model drift, drifts can be characterized as real or virtual. Virtual drifts occur when there is a change in class priors or class distributions that do not affect the class boundaries. Real drifts occur when an actual change in a class boundary occurs.
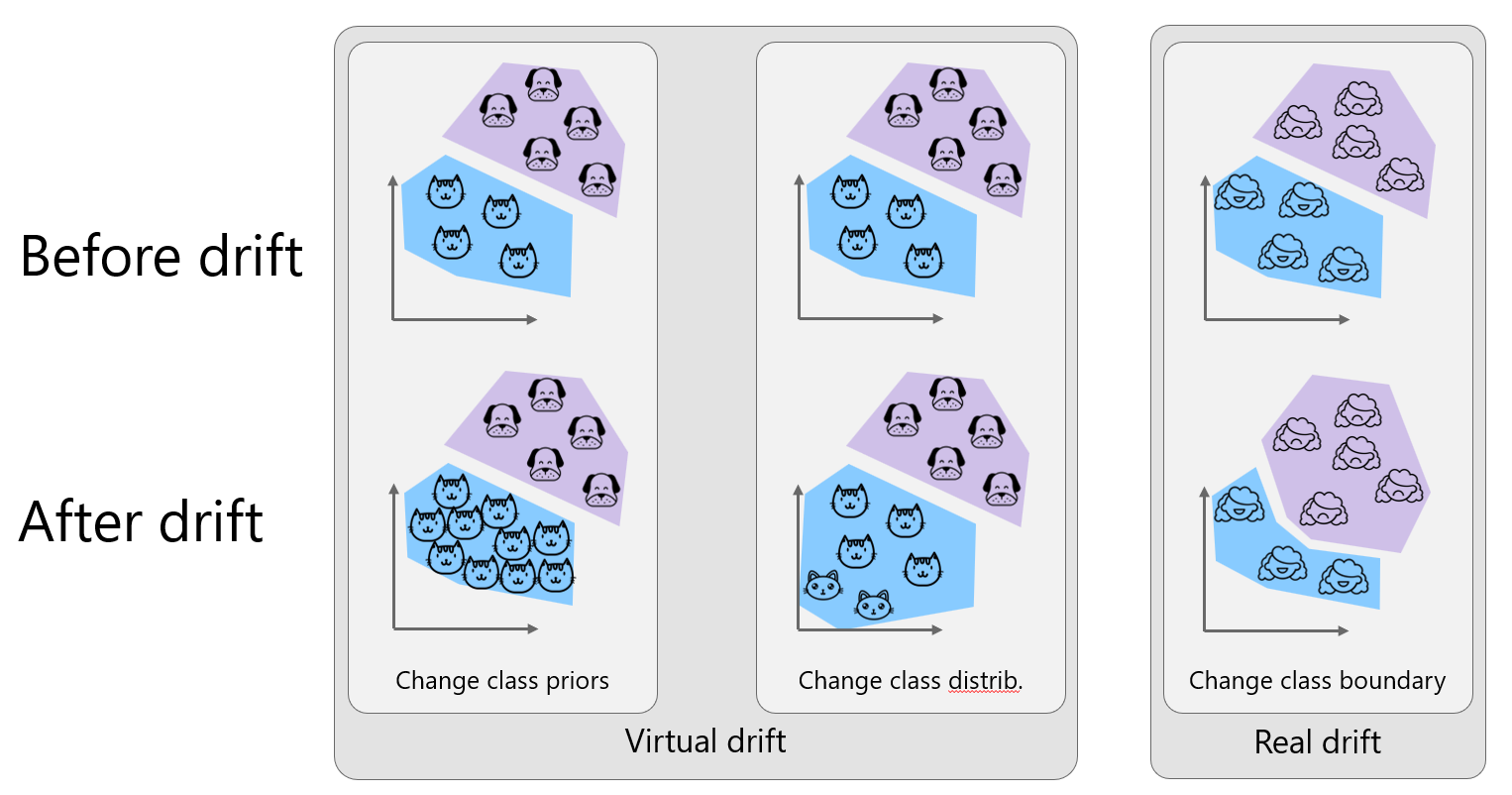
In the first column in the image above, there are more cats in our data after the drift. We’ve changed the class balance and thus priors but aren’t sampling from a new space.
In the second column, some kittens are recorded in the data after drift. There has been no change in the cat/dog boundary, but some feature value distributions (like age and size) have changed in the cat class.
Since the boundary between cats and dogs doesn't really change, even a mellow Pomeranian is still a dog, we will use happiness with a service as our example. After drift, some new features were rolled out that broke some users’ workflows. The result was a formerly happy area is now frustrated. It changes the classification boundary.
The first and second columns represent virtual drift where the class boundary does not change, but the performance of our model may still change. The third column represents real drift.
Drift magnitude
A major drift characteristic is magnitude. Drifts can range from low to high magnitude. Take this simplified example: a low magnitude drift might occur if the age ranges of people most frequently purchasing overalls moves from 20-25 to 30-35. Conversely, a high magnitude drift might occur if the age range changes from 20-25 to 80-85.
Drift duration
Drifts may also range in terms of duration, between abrupt and gradual. For example, cell phone usage patterns drifted gradually over time from mostly audio calls, to mostly mobile internet usage. An abrupt change may occur in buying habits of retail customers, if, for example, there was a popular boycott.
Drift manifestation patterns
Drift can occur incrementally or dispersed and can also be reoccurring. An intuitive way to conceptualize incremental drift is: suppose the concept white is changing to the concept blue. During an incremental drift, white would slowly become darker and darker versions of blue, until the blue concept was fully integrated and the white concept was fully segregated out. A practical example is aging. Humans age incrementally from young to old. In contrast, we do not age in a dispersed manner when we are a baby for 10 years, then an elderly person for two months, a baby again for 7 years, an elderly person for 6 months and so on. Recurring concepts can occur in, for example, retail sales data where holiday season concepts would be expected to reoccur annually.
As one might imagine, different types of drifts can be more easily detected by certain types of methods. The best drift detection strategies are problem-specific. These strategies are often functional on varying different types of drift, since it is not known which drift characteristics are expected. Also many types of drifts can occur in one system. In the following section, we compare and contrast several of the most common drift detection strategies.
How can we detect drift?
Before discussing the details of drift detection methods, it is important to understand the mechanics of managing new data from a stream. We define a stream as any temporally arriving data, including temporally ordered batches. Most drift detection methods employ sliding windows for this purpose. The main idea of sliding windows is to maintain a buffer of part of the stream, typically the most recent part. Often, model adaptation is paired with the sliding window, remembering only the concepts contained within it. The window itself can store actual data points, or more commonly, incremental summary statistics on the data points. Most often, a current window of most recent data is compared to a historical window of data, and if there is a significant difference between the two, a drift is flagged. This is most often based on null hypothesis tests and concentration inequalities. While sliding windows can have many complexities, we will focus on this simple paradigm.
It is clear that window sizes will have a significant effect on the functionality of window-based methods. Window sizes can be either fixed or dynamic. Fixed windows are simple, but they can be problematic. Small sizes are favorable in times of drift for swift adaptation, while large sizes are favorable in times of stability to maximize information. Dynamic windowing permits windows to grow and shrink on the fly based on the current environment, allowing them to be efficient in both periods of drift and stability.
Many drift detection methods employ sliding windows. The following are high-level categories of methods which are not necessarily mutually exclusive:
- Learning-based methods
- Distribution-monitoring methods
- Statistical process control
- Sequential analysis
- Heuristic analysis
Learning-based methods essentially monitor model performance over time, and when model performance degrades, drift is flagged. Some may use multiple models, for example, one trained on a longer window and another trained on a shorter window, and monitor performance differences between them. While these methods have been reasonably successful and give insight into drift, they do have several key drawbacks. The most glaring drawback in the supervised scenario is that, in order to monitor model performance, ground truth labels are required. Obtaining these labels for the whole stream is downright unreasonable (why have a model at all?), and obtaining labels on even parts of the stream can be difficult and costly. Secondly, fluctuations in model performance cannot be attributed to drift alone, so drift might be flagged due to the model not being generalizable enough to one concept. It removes the benefit of understanding the drift characteristics.
Contrarily, distribution monitoring methods do not require labeling, and are more reliable in detecting true drift and providing insight into that drift. These methods are better at describing contributing factors. This family of methods monitors the distribution of the input data, and sometimes the output as well. For example, red shirts typically sell in medium size, then for some reason at some point sales decrease in favor of small red shirts. At that point, distribution monitoring methods determine that drift has occurred and offer explainability about the contributing factors. While distribution monitoring approaches have many advantages, they do not consider the learning system. Thus it is possible to detect drifts that don’t have much of an impact on the system, generating more alerts than necessary. Methods monitoring distributions on output data monitor either the concentration of some uncertainty margin of probabilistic models, or the distribution of output predictions.
Sequential analysis functions under the assumption that drift occurs when the probability of observing subsequences under the historical distribution compared to the recent distribution is beyond some threshold. This threshold may or may not be adaptive. For example, if users frequently perform A, B then C in an app in a historical window, but in a current window, they frequently perform A, B then Z, a drift would be flagged. A major benefit of sequential analysis is that it retains intra-window temporal integrity. However, it is not always directly applicable to all data streaming scenarios.
Statistical process control, or control charts, are commonly applied with the aforementioned methods. Rather than the binary drift or no drift states, control charts additionally employ a transitionary state. Typical system states include:
- In control – stable distribution/stable performance
- Warning – increasing distribution difference/increasing error
- Out of control – significant distribution difference/significant error
The warning period in this process is valuable. It provides a backup model to easily substitute for the current model if there is any drift. Additionally, statistical process control offers an inherent measure of the rate of change of the system: time between warning and out of control states. A drawback of determining thresholds for each state, even dynamically, can be challenging and does have a significant effect on the success of the system.
Heuristic analysis is the least complex of the methods discussed, and is typically not used in isolation. They are rules-based drift flags that are domain-specific. An example is to flag change if the temperature of an IOT device reaches a particular value. This method should not be confused with data validation procedures. In this example, the rising temperature should indicate a true drift, like a changing season, not a defective device. Heuristics analysis is a simple way to capture domain knowledge of drifts, but if rules become too complex, it is reasonable to use other approaches.
How can we adapt to drift?
Models account for drift by adapting. The most fundamental elements of model adaptation are remembering and forgetting. The most basic way of solving the drift problem is: at a regular specified time interval, discard the model and replace it with a new one, trained on data collected within a specified time frame. It is referred to as blind global replacement. Blind adaptations do not use adaptation triggers and update on recent data, which may or may not be relevant. This is in contrast with informed adaptation strategies. Global replacement, as opposed to local replacement, refers to the entire model being discarded and reconstructed from scratch. Do note that for supervised learning tasks, the new data used to train the replacement model is required to be labeled. This approach is currently the most typical for drift in industry today.
Blind global replacement strategies come with a host of issues. The first challenge is determining a relevant retrain cadence. In some applications, this decision may be more informed than others. For example, it might make sense to replace a tax model once per year. But it is challenging to determine how frequently to replace a model that makes hourly predictions. It highlights another challenge: global replacement is expensive. It takes time and resources to build an entirely new model from scratch. When we are ready to build a new model from scratch, how do we know which data to train it on? The assumption that recent data is most relevant is correct, but how should we decide which recent data to train on and how far back should be remembered?
For example, suppose you have a daily retrain cadence and you've replaced a model. Suppose a drift occurs one hour after retrain. It means that your model will likely be making erroneous predictions for a full 23 hours before you retrain again. Another challenge arises when deciding which data window to use for retraining to ensure that the new model accurately represents the current data. Perhaps, as a rule, you always retrain on the last 3 days' worth of data. Will your new model know enough about the current concept to be performant, or will it still be too diluted with the old concept from the previous 2 days? These issues are all important and difficult to resolve in the context of a blind global replacement, which may contribute to sub-optimal performance.
Drift detection permits informed adaptation, as opposed to blind adaptation, where the model can adapt at the right time and on data that reflects the current concept. While this informed adaptation can guide decisions around which data to retrain on, there is an even better solution: train on all of the data and forget what’s irrelevant on the fly.
Online incremental learning algorithms update the model upon arrival of each data point (or sometimes mini-batches – let's focus on the data-point-by-data-point architecture for now). These algorithms may adapt implicitly just by learning on increasingly more recent data. Or they may use blind forgetting with a specified periodicity. They could also adapt in an informed manner using drift detection triggers. Some learners’ mechanics only permit them to forget globally, like Naïve Bayes. Others permit local replacement, like decision trees or ensembles. Local replacement involves discarding irrelevant subsections of models to replace them with relevant subsections. If there are re-occurring concepts, inactive models may be stored and re-activated upon re-emergence of the concept that they reflect.