Solver/Portfolio Optimization: How to use Solver to get the highest sharpe ratio and how to answer the questions under the three scenarios?

Question

This is the data I have: 

Does anyone know how I can use Solver on Excel to find the highest Sharpe ratio?

In addition, I'm supposed to provide separate answers under each of the following scenarios.

A)  All the portfolio weights must be non-negative. 

B) Non-negative weights + No investment in the mom return.

C) Non-negative weights + No investment in Gold. 

 I believe I need to start by creating three columns for the portfolio returns. But I'm not entirely sure how to do this. If anyone has any idea on how I can do that and answer the questions under the three scenarios, or the direction I should take to get this done. It would be so helpful and appreciated.

Answer 1

Hi Farah,

Thanks for choosing Microsoft.

According to your description, it seems that you would like to use Solver to get the highest Sharpe ratio, we are willing to investigate your issue.

Based on your data, I create a new sheet and I can use the sort feature to get the highest Protofolio Returns. See Quick start: Sort data in an Excel worksheet

As I’m not sure what’s the meaning of Sharpe ratio or how you get the Sharpe ratio, could you please tell us more details and if convenient, please upload a sample file to OneDrive and share the link with us.

Share OneDrive files and folders

Regarding to your three questions, may I know what do you mean portfolio weights?

Appreciate your time and effort to share the above information with us. :)

Best regards,

Gloria

Answer 2

Hi.  You asked a similar question a week or so ago, but didn't give much information to work with.

Is this a class project?  Just curious what information they gave for the problem.

I am not an expert here, and I haven't done these in a while.

First question would be:

Market return in Feb-70 was 1161% for the month?   As a number, it would be displayed as you have:  11.61.

So, I would question your data to start.

My guess is that Market, and Portfolio are not important to the question.

Here's the "general" outline, but I am not sure about monthly returns vs yearly returns.

So, in general...

I am using a small sample.  Rows: 1-5 only. You have means of your returns:  ( I use range names )

You then need a Covariance Matrix.  I'll call this "M"

Start with weights of 20%.  These are the cells solver will change.

Your expected return is the weights * avr return.

(MMULT if orientation differently, Sumproduct if same orientation. )

I "assumed" RiskFree is the TBills.

I am not clear at the moment if you need to adjust to annual returns or not... I don't remember.

Here are 2 ways for the Sharpe ration.  Pick the one they mention in class.

Solver:  Maximize Sharpe, 

Adjustable cells:  Weights

Constraints:  0 <= Weights <= 1

Total Weights = 1

So, this may not be perfect, but it may give you direction depending on what they say in class.

Answer 3

Dana wrote:

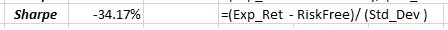
There seems to be some disagreement about the Sharpe denominator, at least among non-authoritative online sources. Even individual websites are inconsistent within themselves.

Dana uses the stdev of just the portfolio returns (R).  And according to the wikipage for "Sharpe ratio", that was indeed the original definition of the Sharpe ratio in 1966.

But in 1994, Sharpe updated the definition, using instead the stdev of R - Rf, where Rf is the return(s) for a risk-free investment or benchmark.

As the wikipage points out, stdev(R) = stdev(R - Rf) when a single Rf is used, as Dana does.

But when Rf[i] is provided for each R[i], as in Farah's data, stdev(R) <> stdev(R[i] - Rf[i]).  And the latter should be used.

(In another discussion of the same problem, Farah indicates that the T-bill returns should be used for Rf.)

For Dana's example (a subset of Farah's data), the difference is:

Sharpe = (mean(R) - Rf) / stdev(R) = -0.341700194655291

Sharpe = (mean(R) - Rf) / stdev(R[i] - Rf[i]) = -0.346832441888126

Not a big difference for Dana's example. I don't know about Farah's complete example.

I might also note that it makes no difference in the Sharpe numerator.  That is, mean(R[i] - Rf[i]) = mean(R[i] - Rf) = mean(R) - Rf, regardless of whether Rf is mean(Rf[i]) as Dana uses, or Rf is an arbitrary value.

Dana wrote:

First question would be: Market return in Feb-70 was 1161% for the month?   As a number, it would be displayed as you have:  11.61. So, I would question your data to start.

The data appears to be rates of returns, expressed as percentage times 100 (sigh).  So there is no issue.

The Sharpe ratio is the same whether we use the returns as Farah posted them, or we divide them by 100 (copy 100 and paste-divide), formatted as Percentage.

I discourage the presentation of percentages times 100.  Although it makes no difference for the Sharpe ratio, there are other calculations that require that we use 1+r, where "r" is the percentage change.  And while that makes "good sense" (to most of us), it does not seem intuitive to write 100+r, where "r" is the percentage change times 100.

Dana wrote:

I am not sure about monthly returns vs yearly returns.

There also seems to be some disagreement about that among non-authoritative online sources.

But one example on the wikipage for "Sharpe ratio" shows weekly data without annualizing.

So it seems that annualizing subannual returns is not required; and I would discourage it.

Dana wrote:

I have never understood the need to calculate the portfolio stdev with a formula like that, if we have access to the raw data, as Farah does and Dana relied upon.

We can avoid the complication of calculating a covariance matrix by calculating the portfolio stdev directly from the data, in one of several ways.

This is demonstrated in the image below.  You may download the file sharpe ratio answers-ms.xslx .  Ignore any preview errors; and a login is __not__ required.  Just proceed to download the file.

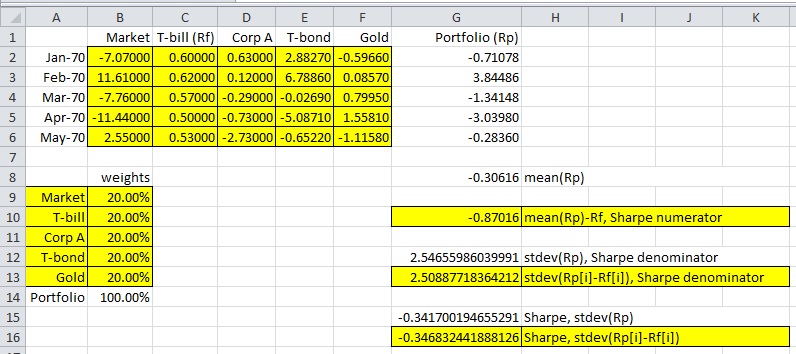
Formulas:

G2: =MMULT(B2:F2, $B$9:$B$13)

Copy G2 into G3:G6

G8: =AVERAGE(G2:G6)

G10: =AVERAGE(G2:G6) - AVERAGE(C2:C6)

G12: =STDEV(G2:G6)

G13: =STDEV(INDEX(G2:G6-C2:C6, 0, 1))

G15: =G10/G12

G16: =G10/G13

---

As a proof of concept, compare the stdev(Rp) in G12 above with stdev(Rp) in N9 below, based on the covariance matrix.

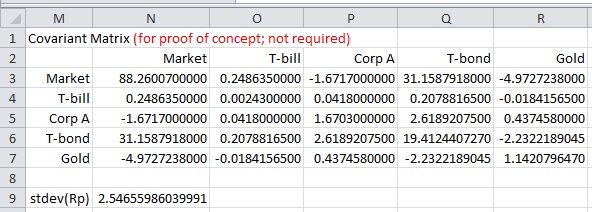
Formulas:

N3: =COVARIANCE.S(INDEX($B$2:$F$6, 0, ROWS($N$3:N3)), B$2:B$6)

Copy N3 into N3:R7

N9: =SQRT(SUMPRODUCT(MMULT(N3:R7, B9:B13), B9:B13))