Genetic Algorithms
Survival of the Fittest: Natural Selection with Windows Forms
Brian Connolly
This article discusses:
|
This article uses the following technologies: Windows, C#, and CodeDOM |
Code download available at:GeneticAlgorithms.exe(190 KB)
Contents
The Sample Problem
The Application UI
High-Level Class Design
Genetic Programming
Ant Class
TerminationReport Class
Function Class
ExpressionTree Class
Generator Class—Constructor
Generator Class—Replicate and Breed Children
Generator Class—Generating New Classes
Generator Class—Compiling New Code and Executing It
Building and Running the Application
Working with a Complex Problem
Further Work and Extensions
Genetic programming (GP) is one of the most useful, general-purpose problem solving techniques available to developers. It has been used to solve a wide range of problems, such as symbolic regression, data mining, optimization, and emergent behavior in biological communities.
GP is one instance of the class of techniques called evolutionary algorithms, which are based on insights from the study of natural selection and evolution. Living things are extraordinarily complex, far more so than even the most advanced systems designed by humans. Evolutionary algorithms solve problems not by explicit design and analysis, but by a process akin to natural selection.
An evolutionary algorithm solves a problem by first generating a large number of random problem solvers (programs). Each problem solver is executed and rated according to a fitness metric defined by the developer. In the same way that evolution in nature results from natural selection, an evolutionary algorithm selects the best problem solvers in each generation and breeds them.
Genetic programming and genetic algorithms are two different evolutionary algorithms. Genetic algorithms involve encoded strings that represent particular problem solutions. These encoded strings are run through a simulator and the best strings are mixed to form a new generation. Genetic programming, the subject of this article, follows a different approach. Instead of encoding a representation of a solution, GP breeds executable computer programs.
In this article I'll take a simple GP problem from the seminal textbook on the subject: John Koza's Genetic Programming: On the Programming of Computers by Means of Natural Selection (MIT Press, 1992). The problem is to develop an artificial ant that will efficiently walk a grid that has a weaving trail of food on it. The objective is to breed the ant that will gather the maximum amount of food in the minimum number of steps.
I'll develop a UI that displays the problem grid and allows the user to control GP execution. The UI can be used to study the successive generations of ants. Any ant from any generation can be selected for study. Its generated C# code can be viewed, and the trail that it walked can be displayed on the grid.
The internal process works off of a base class that represents the problem. In this case, I developed a base ant class that implements the fundamental operations and state of an ant. The GP algorithm is used in order to breed new subclasses of this problem class. The algorithm uses the code document object model (CodeDOM) to generate a subclass and an Execute method implementation that represents a possible strategy for an ant.
This implementation is generic in the sense that it is driven entirely by a master "problem" class (the base Ant class). A developer can specify a new GP problem class that is modeled after the Ant class. For example, this might be a class representing the allowable functions for a symbolic regression problem. Since the internal GP processing doesn't have any special-purpose ant logic, the same architecture could be used to solve that problem as well.
I developed this implementation to demonstrate that the Microsoft® .NET Framework provides all of the tools that you need to do genetic programming. While this implementation meets all of the essential requirements to qualify as genetic programming, in its present state there is plenty of room for the solution to be augmented and improved. For example, complex selection, mutation, and pruning techniques could be used to explore the solution space far more thoroughly than does this simple example. But since they are essentially just mathematical refinements of the basic algorithm, this article demonstrates that .NET-based GP implementations can reach that level of sophistication.
In this article, I will describe the sample GP problem we'll be working with and will walk through the class relationships and the key implementation code. I'll also give you an overview of genetic programming and show you how ants can be evolved to walk a more complex trail, as well as how you can make changes to the problem class to make new operations available.
The Sample Problem
The abstract problem I'll deal with is to develop an intelligent strategy to be used by a simple artificial ant. The ant moves on a 32¥32 grid, and if it moves off one side it returns on the other side. The grid has a winding trail of food on it. The trail begins at the [0,0] origin, which is also the starting position of the ant. Each grid location in the trail can be empty, contain food, or contain an indicator that it is a gap between food locations. The trail must be continuous from the origin. All food must be adjacent to at least one point that has food or a marked gap.
The simple ant has two elements that fully describe its state. The first is its current location on the grid. The second is the direction it is facing, which is either left, right, up, or down. The ant has three possible things it can do. It can turn left, turn right, or move to the square that it is facing. It has only one sensor for its environment: a function called FacingFood which will tell it if there is food in the square that it is facing.
When an ant moves to a square that contains food, it removes the food from the grid and increments the total food it has gathered. When it moves or turns, it increments the number of steps it has taken to gather its food.
The problem is to create an ant that will make an intelligent series of moves and turns based on its FacingFood function. An example would be:
if (FacingFood()) { Move(); } else { TurnRight(); Move(); }
This would work fine for trails whose turns are always to the right. The practical problem is to use GP to create a program that will walk an arbitrary trail of food and gaps most efficiently.
The Application UI
Figure 1 shows the UI of the .NET-based implementation of the artificial ant. The grid panel is divided into a 32¥32 matrix of squares that contain the trail of food to be retrieved by the ant algorithm. A default trail is loaded at startup. You can use the "Empty Grid" button to remove the trail. The Food and Gap radio buttons allow the user to paint a new trail by clicking in the grid. The "SaveGrid" button outputs the current grid trail to an XML file, which can later be loaded back in with the "Restore Grid" button.
Figure 1 Artificial Ant Application Window
.gif)
The boxes on the left control GP execution and include the following:
Generations The algorithm will stop after this number of generations is produced. However, if a perfect ant (an ant that gathers the maximum amount of food in the minimum number of steps) is discovered, the algorithm will immediately halt execution.
Population This is the number of ants each generation will have. The population will be a mixture of the most efficient ants from the previous generation, together with their children.
Max Tree Depth The algorithm begins by generating random ants. This setting controls how deep their expression trees can be.
Food Goal and Step Goal We'd like to breed an ant that will gather this much food in these few steps. By default, these will reflect the food and gap counts in the active grid. However, the computed Step Goal doesn't reflect the turn operations that an ant will need to make when the trail changes direction.
In order to demonstrate the UI and application, let's work through a simple example. Start the application, which should look like Figure 1. There are gap squares that break the connection between the smaller food square to the upper left and the larger food square next to it.
The two squares have a total of 33 food cells and, since there are two gaps, the minimum possible number of steps required to obtain all the food is 35. Recall that the minimum step total doesn't reflect turn operations that are necessary at corners.
Hit the Generate button with the default textbox parameters to start the genetic programming process. This will generate an initial population of 100 ants, each of which will follow a randomly generated strategy. Here, Max Tree Depth is set to 5, so the initial population of ants will have at most five levels of conditional branching, moves, and steps.
The listbox beneath the Generate button shows summary data about each generation. This is the average "fitness" of the generation, and the fitness of the best and worst ants. I'll define fitness later; at this point all that's necessary is that you realize that higher fitness is better.
When the tenth generation is completed, select the generation summary from Generation 1, and all of the ants in that generation appear in the listbox beneath it. Each ant represents a randomly generated class. The name of each ant is shown with the amount of food it gathered and the number of steps it took. The name of the ant class is GenX_AntY, where X is the generation number and Y is the ant number within that generation. The best ant from a generation always appears at the top of the listbox. Select that top ant from Generation 1.
When an ant is selected, detailed information about it is displayed in the textbox beneath it. This will show the parents of the ant—that is, the name of the classes from which it was generated. Below the list of the parents, the generated code for the selected ant will be listed. I'll describe the code in more detail later.
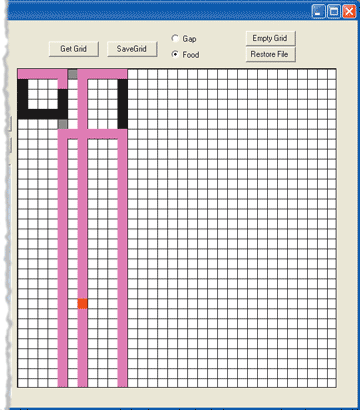
Figure 2** Poor Performance **
When an ant is selected, two buttons are activated. Replay Step allows the user to step slowly through the trail that the ant made, one move at a time. Replay All automatically walks the entire trail. Figure 2 shows the UI display when Replay All is clicked for the best ant in Generation 1. The generated code, the lineage information about ants, and the display of the trail they took provide excellent tools for studying a genetic algorithm. The best ant in Generation 1 gathered only 18 items of food, taking the maximum allowable 400 steps. Its trail display in Figure 2 shows why it is so poor. Note that since the logic for each ant is generated with some degree of randomness, your results may vary slightly.
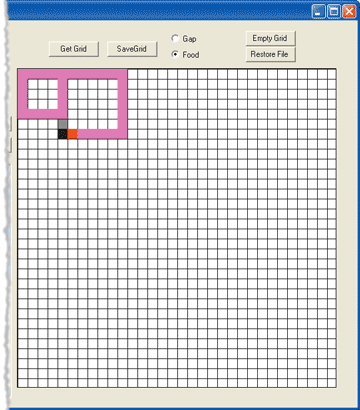
Figure 3** Ant Trail in 45 Steps **
Next, scroll down the Generations listbox to select Generation 10. Select its best ant, the one at the top of the ant listbox. This ant evolved by selecting and combining the most efficient food gatherers from prior generations. This ant gathered 33 items of food in only 45 steps. Its trail is displayed in Figure 3. Clearly it is following a strategy that is far more efficient for this trail.
High-Level Class Design
A high-level view of the class design is shown in Figure 4. Several of the classes I use, such as the Cell, AntTrailGrid, TerminationReport, IComparable, mFoodGathered, and Ant, are problem specific. If you wanted to use the kernel of this implementation for another problem space, you would need to develop different versions of these classes. However, the Generator, Function, and ExpressionTree classes that together form the core of the GP algorithm can remain essentially unchanged.
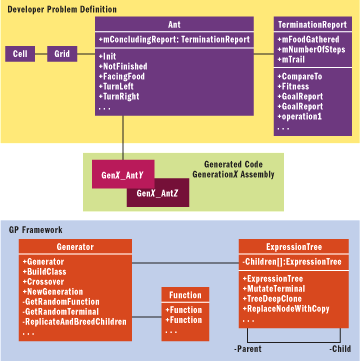
Figure 4** Class Design **
The Cell class represents a grid cell. The AntTrailGrid class is used to perform graphics operations on the display grid panel. I won't describe these classes in detail as they pertain more to the user interface than to GP.
The Ant class and its associated TerminatingReport class represent the problem I'm trying to solve. An Ant is initialized by passing a grid, a food goal, and a limit on the number of steps it will take. In my implementation I limit every ant to 400 steps. The Ant has public methods to turn and move, and private member variables to record the steps taken and food gathered as it moves through its grid. The Ant also maintains a history of where it's been on the grid in the private mTrail ArrayList. It also has a single, Boolean function: FacingFood.
Whenever an ant takes a step, it checks to see if it has reached its food goal or if it has taken the maximum number of steps allowed. If one of these is true, it saves its history in the member variable mConcludingReport, a TerminationReport. The TerminationReport records the food and step counts, and also saves the trail of the ant. The Fitness method of TerminationReport implements the fitness measure of an ant by returning an integer score that accounts for the food gathered and the steps taken. Ants that gather more food in fewer steps are more fit than other Ants that perform worse. TerminationReport also implements the CompareTo method of the IComparable interface. The CompareTo method compares TerminationReports according to fitness. When a generation completes, the Generator class will have hundreds or even thousands of TerminationReport instances in an ArrayList, and the IComparable implementation allows the ArrayList to be sorted by fitness.
Generator is the kernel of the GP implementation. It performs selection, breeding, code generation, execution, and result sorting. A generator is constructed by passing a BaseClass type (the Ant class, in this case), and a maximum expression tree depth limit. It uses reflection on the BaseClass type to find all of its public methods that have no parameters with the exception of the special NotFinished method. All of the void methods will be the primitive operations available for the GP algorithm to employ. Any Boolean methods with no parameters are used to control the execution of the primitive operators. This information is stored in Function objects. When NewGeneration is called requesting an initial population of N ants, it builds N random ExpressionTree objects. Generator uses these ExpressionTrees and CodeDOM classes to construct N subclasses of Ant, each of which has a single method called Execute. The Execute method has a loop of the expression tree statements that are executed as long as the NotFinished method returns true.
Generator places all of these classes in a single namespace, compiles them, and loads this new assembly. It then creates a single instance of each generated class, invokes its Execute method, and saves the TerminationReport. In a more robust implementation, each assembly would be isolated in its own AppDomain so that it could be unloaded when no longer needed. For demo purposes, I've chosen to keep things simple and to load all assemblies into the main AppDomain.
TerminationReport has a single, static method called GoalException. Generator uses this to create a special instance of the TerminationReport. This instance will have the same fitness as a perfect ant—one that gathered all available food in the minimum number of steps. Generator will continue with successive generations, performing selection and crossover breeding until it reaches the generation limit or it evolves a perfect ant.
Generator is a general-purpose implementation of GP. I stated earlier that you could define a different problem as a different "ant." Perhaps this ant would expose a set of primitive mathematical functions such as addition, multiplication, and exponentiation. Its grid would be a set of (x,y) input and output values from a function for which you would need to develop a mathematical expression. You could then essentially use Generator without change to solve this problem as well.
To be truly generic, the design needs to be changed, but only slightly. Generator uses TerminationReport directly to construct the goal exception of the perfect ant, and it also has some knowledge of the Init method that is used to pass the Grid to the ants that it instantiates. In the detailed discussion of Generator that follows, I'll describe what is needed to make it truly generic instead.
Genetic Programming
In his textbook, John Koza presented a large number of sample problems that can be solved with genetic programming. He developed a systematic way of relating particular problems to a canonical set of design decisions that a developer uses to model a problem.
One step is the selection of what he calls terminals and functions. The ant will be controlled by behavior expressions, which are tree-like structures of terminals and functions. Terminals are primitive operations or literals that cannot be decomposed further. Functions are higher-level operations that use other functions or terminals. In our case, the artificial ant has terminals Left, Right, and Move. One member of the function set is the FacingFood Boolean, which takes two terminal or function arguments. The statement "if FacingFood, then Left else Right" is an example of an expression that has the function FacingFood and two children: the terminals Left and Right. I'll also generate two other functions. The first, which I'll call P2, has two clauses which are themselves either terminals or functions. An example of this is the expression "Right;Move". A second function that I'll add is P3. This is just like P2, except that it has three clauses. An example of P3 is the expression "Move; Right; if FacingFood then Right else Move".
The GP algorithm begins by generating a population of random expressions. One parameter that controls the algorithm is population size; this is one of the parameters that the user can set in the UI. These expressions are then executed and evaluated, using a fitness measure. Designing this fitness measure is another step in the canonical GP design fitness criteria. I want to select efficient ants, those that gather a lot of food with few steps, so the fitness measure weighs both food gathered and the number of steps used. In my implementation, I subtract the steps from the food gathered and add 1000, so that fitness is always positive. Hence an ant with a higher fitness measure is going to be more successful than an ant with a lower measure.
When the initial, random first generation is completed, the real work of GP begins. The first step is selection, which is choosing the best ants and copying them to the next generation. Most GP implementations use one of a number of sophisticated selection techniques, but for the sake of simplicity this implementation copies the best 10 percent, as measured by our fitness criteria. These selected ants will be the "parents" of all the remaining ants in the subsequent generation.
Subsequent generations begin with the pool of parents that were replicated from the prior generation. Since this is only 10 percent of the available population, I need to fill the remaining slots by selecting parents and breeding them to create the next generation. Pairs of parents are selected, and each pair of parents yields a pair of children, each of which combines elements of both parents. Parents are selected according to fitness. In general, fitter parents are more likely to be selected to breed.
The crossover algorithm (see Figure 5) is used to breed a pair of children from a pair of parents. A random crossover point is chosen in each parent, and the subtree beneath these crossover points is swapped between the parents, creating the two offspring.
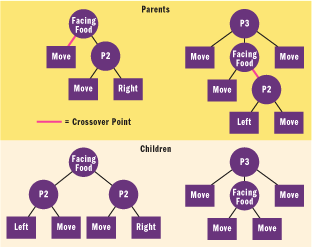
Figure 5** Crossover (Breeding) Operation **
Most GP algorithms also implement mutation. This involves making a random change in a small number of offspring in order to maintain diversity in the population. Mutation is essential because otherwise the population becomes completely dominated by a few good bloodlines, which makes it difficult to continue progress beyond a certain point. This implementation performs a simple mutation step during the crossover operation to introduce randomness. When a terminal node is copied, a random terminal is substituted two percent of the time.
Ant Class
An Ant is initialized by passing it a reference to a grid, integers that specify the food goal, and the maximum number of steps:
public Void Init(Cell[,] grid, int StepLimit, int FoodGoal)
The ant places itself at the [0,0] origin and faces right. When an ant walks the grid, it removes any food it gathers. For this reason it makes its own copy of the grid.
The turn and move methods are simple. For example, the Move method moves to the facing grid location, increments the number of steps, and checks to see if it should terminate, as you can see if you take a look at Figure 6.
Figure 6 Move Method
public void Move() { if(NotFinished()) { GetFacingCellCoord(outxLocation, outyLocation); mTrail.Add(newTrailSpace(xLocation, yLocation)); mTotalSteps++; if(mGrid[xLocation,yLocation].HasFood()) { //gather the food and remove it from the grid mTotalFood++; mGrid[xLocation,yLocation].SetEmpty(); } }
The NotFinished method checks for completion and saves a concluding TerminationReport:
public bool NotFinished() { if (!mDone) { if (mTotalSteps==mStepLimit | mTotalFood==mFoodGoal) { mConcludingReport= new TerminationReport( mTotalSteps,mTotalFood,mTrail); mDone=true; } } return !mDone;
TerminationReport Class
TerminationReport is used to save the history of ant executions and to compare the relative fitness of ants. It exposes a Fitness method that returns a positive measure of an ant's fitness:
public static int Fitness(TerminationReport RunResult) { // more food and/or fewer steps is better. // we add 1000 so that it's always positive return RunResult.mFoodGathered - RunResult.mNumberOfSteps + 1000; }
The IComparable interface CompareTo method uses this fitness value to determine the relative order of ants. This allows Collections of TerminationReports to be sorted by fitness:
public int CompareTo(object obj) { if(obj is TerminationReport) { TerminationReport temp = (TerminationReport)obj; return Fitness(this).CompareTo(Fitness(temp)); } throw new ArgumentException( "object is not a TerminationReport"); }
Function Class
The Function class is a private class that a Generator uses to represent the available functions from the base problem class. There are two types of functions:
- If statements represent the Boolean-valued methods from the base class. In the ant application, this represents the FacingFood method.
- Child count functions hold slots for a defined number of child functions or terminals. Examples of these would be the P2 and P3 internal tree nodes in Figure 5.
Function has two constructors corresponding to these two types:
public Function(MethodInfo methodInfo) { mFunctionType = FunctionType.IfStatement; mMethodInfo = methodInfo; mChildCount = 2; } public Function(int childCount) { mFunctionType = FunctionType.ChildCount; mChildCount = childCount; }
MethodInfo is the reflection information on a method that the Generator gets from the base problem class. The code assumes that any Boolean-valued function can be used as the condition in an If statement (except for the special NotFinished function).
The set of Function objects created by the Generator remain unchanged during GP processing. These objects control the types of manipulation it can perform on ExpressionTrees which are the dynamic objects that represent potential solutions to the problem.
ExpressionTree Class
The program will generate ants that repeatedly perform a set of moves and turns, subject to checks of the FacingFood condition. These operations are represented internally by an ExpressionTree for each ant. ExpressionTrees are used to generate C# code and are the subject of selection and reproduction.
ExpressionTree has a single constructor, shown in Figure 7. This builds a random tree from the set of Functions and an ArrayList of terminals. MaxDepth controls how deep the tree can grow—when it reaches that point, only terminals can be selected for the next level. ExpressionTree also exposes methods to create a new copy of a tree node and also to clone the entire tree. These are used to implement the crossover operation.
Figure 7 ExpressionTree Constructor
// generate a random ExpressionTree from the set of // terminals and nodes we found in mBaseType. The // tree will be at most MaxDepth levels deep public ExpressionTree (int MaxDepth, Generator Generator, Object Node, Object Parent) { mNode = Node; mParent = Parent; if(mNode.GetType() == typeof(Function)) { Function mFunction = (Function)mNode; mChildren = new ExpressionTree[mFunction.ChildCount]; for( int i = 0; i< mFunction.ChildCount; i++) { if (MaxDepth > 0) { mChildren[i] = new ExpressionTree (MaxDepth-1,Generator, Generator. GetRandomTerminalOrFunction(), this); } // if we've reached MaxDepth, choose only // terminals else { mChildren[i] = new ExpressionTree( MaxDepth-1,Generator, Generator.GetRandomTerminal(), this); } } } }
Generator Class—Constructor
The Generator class is the kernel of the genetic programming application. It discovers available base class terminals and functions. It generates, compiles, and executes C# code to search for a good solution to the problem it is given. The constructor is passed a System.Type which is the root class for .NET reflection operations. In this case, the Type is Ant. The Generator constructor fills the list of terminals and functions, treating void methods as terminals and Boolean methods as Functions (see Figure 8). After it does this, the final for loop adds some additional functions. This application passes a MaxSteps value of 3, which makes the generator add two additional functions. The first will have two children; the second will have three children.
Figure 8 Generator Constructor
public Generator(Type BaseClass, int MaxSteps) { mBaseType = BaseClass; mTerminals = new ArrayList(); mFunctions = new ArrayList(); // first create the terminals BindingFlags flags = BindingFlags.Public | BindingFlags.Instance; MethodInfo[] mBaseClassMethods = BaseClass.GetMethods(flags); foreach(MethodInfo mi in mBaseClassMethods) { // Terminals are parameterless void methods, except // for "Execute" if(mi.GetParameters().Length == 0 && mi.ReturnType == typeof(void) && mi.Name != "Execute") { mTerminals.Add(mi); } else if(mi.GetParameters().Length == 0 && mi.ReturnType == typeof(bool) && mi.Name != "NotFinished") { mFunctions.Add(new Function(mi)); } } for(int i = 2; i<= MaxSteps; i++) { mFunctions.Add(new Function(i)); } }
Generator Class—Replicate and Breed Children
When the user clicks on the Generate button, the form object calls a Generator method called NewGeneration, once for each generation. NewGeneration controls the evolution towards the problem solution. NewGeneration returns a result object that contains a summary of the generation, as well as all of the TerminationReport objects exposed by its ants. When the form object calls NewGeneration again, it passes back this result object.
NewGeneration begins by calling a private method called ReplicateAndBreedChildren. This method handles two cases. The first case is when it is working on the first generation. It creates new, random expression trees, assigns class names to the ants that will be generated from them, and creates new result objects that will hold their execution results when they've been executed:
// first generation - just generate random trees for(int i = 0; i<= NumberOfPrograms-1;i++) { ExpressionTree newTree = new ExpressionTree( MaxTreeDepth,this, GetRandomFunction(), null); string temp = NewAntName ( GenerationNumber, i); ThisGenerationResults.Add( new TypeExecutionResult(NewAntName(GenerationNumber, i), "","",newTree)); }
The other case is when there are results from the last generation. First, we need to select the best ants from the prior generation and copy them into this generation. GenerationResults is an ArrayList that contains a TerminationReport for each ant. The ArrayList.Sort method ultimately invokes the TerminatingReport.CompareTo method which compares ants by fitness. Since better ants have higher fitness measures, we reverse the sort to place the best ants in the lower slots (the sorting comparison operation could also be inverted to do this implicitly, which would be more efficient), and we keep 10 percent of them in the current generation:
int numToKeep = NumberOfPrograms/10; int numKept = 0; LastGenerationResults.Sort(); LastGenerationResults.Reverse(); IEnumerator enumLastGenerationResults = LastGenerationResults.GetEnumerator(); while(enumLastGenerationResults.MoveNext() && numKept++ < numToKeep) { ThisGenerationResults.Add((TypeExecutionResult) enumLastGenerationResults.Current); }
Next, we need to fill the remaining population slots with children. Pairs of parents are selected, and the Crossover method is used to create new children using the algorithm just described. Parents are selected based on their relative fitness. The probability of selecting a particular parent is the ratio of that parent's fitness, divided by the total fitness of all parents. Figure 9 shows the Generator.ReplicateAndBreedChildren code for this processing.
Figure 9 Generator Select-And-Breed
// breed two children for each pair of parents // until we've filled all the slots for(int i = ThisGenerationResults.Count; i<= NumberOfPrograms-2; i=i+2) { ExpressionTree child1, child2; ExpressionTree Parent1, Parent2; int Parent1Index, Parent2Index; SelectParentsAndCloneThem (ThisGenerationResults,numKept - 1, out Parent1Index, out Parent1, out Parent2Index, out Parent2); Crossover (Parent1, Parent2, out child1, out child2); TypeExecutionResult childResult1, childResult2; childResult1 = new TypeExecutionResult ( NewAntName(GenerationNumber, i), ((TypeExecutionResult) ThisGenerationResults[Parent1Index]) .mTypeClassName, ((TypeExecutionResult) ThisGenerationResults[Parent2Index]) .mTypeClassName, child1 ); childResult2 = new TypeExecutionResult ( NewAntName(GenerationNumber, i+1), ((TypeExecutionResult) ThisGenerationResults[Parent1Index]) .mTypeClassName, ((TypeExecutionResult) ThisGenerationResults[Parent2Index]) .mTypeClassName, child2 ); ThisGenerationResults.Add(childResult1); ThisGenerationResults.Add(childResult2); }
Generator Class—Generating New Classes
Generating executable code is the essence of genetic programming because that is what distinguishes it from other evolutionary algorithms. This application uses CodeDOM to create a CodeCompileUnit containing a class for each ant in a generation, and it uses the Microsoft.CSharp.CSharpCodeProvider to create an ICodeGenerator and an ICodeCompiler.
First let's look at the type of class we want to create. An example of a particular generated ant is shown in Figure 10. A subclass of Ant is declared, and the name of the class includes the generation number and the ant number within that generation. The Ant subclass has an Execute method that overrides the abstract Execute method in the base Ant class. It contains a loop that continues as long as NotFinished returns true. The loop consists of a series of statements that invoke base class methods and functions, and it is this series of statements that will be created from the ExpressionTree corresponding to the Ant.
Figure 10 Sample Generated Ant
public class Ant_Gen1_Ant33 : Ant { public override void Execute() { for ( ; NotFinished(); ) { if (FacingFood()) { Move(); } else { TurnRight(); if (FacingFood()) { Move(); TurnLeft(); } else { Move(); TurnLeft(); } } } } }
The Generator has a public BuildClass method that generates this class, given an ExpressionTree. It is public because the main form uses this method to fill the contents of the code textbox when an ant is selected for examination. BuildClass creates the class declaration and adds the base type property. It calls BuildExecute to create the Execute method from the ExpressionTree:
publicCodeTypeDeclaration BuildClass(string ClassName,ExpressionTree tree) { CodeTypeDeclarationmType =new CodeTypeDeclaration(className); //it inherits from mBaseType; mType.BaseTypes.Add(mBaseType.Name); mType.Members.Add(BuildExecute(Tree)); return mType; }
BuildExecute calls GenerateStatements to build the statements of the loop and passes to it the ExpressionTree. The code for BuildExecute is shown in Figure 11, and the code for GenerateStatements is shown in Figure 12.
Figure 12 GenerateStatements
// generate the statements that express the terminals and // functions of the Tree private CodeStatement[] GenerateStatements (ExpressionTree Tree) { CodeStatementCollection mCodeStatements = new CodeStatementCollection(); Object mNode = Tree.Node; if ((System.Type)mNode.GetType() == typeof(Function)) { Function mFunction = (Function)mNode; if (mFunction.FunctionType == FunctionType.IfStatement) { CodeSnippetExpression ifcondition = new CodeSnippetExpression( mFunction.MethodInfo.Name.ToString() + "()"); CodeStatement[] cstrue = GenerateStatements(Tree.Children[0]); CodeStatement[] csfalse = GenerateStatements(Tree.Children[1]); CodeConditionStatement ifStatement = new CodeConditionStatement (ifcondition, cstrue, csfalse); mCodeStatements.Add(ifStatement); } else { for( int c = Tree.Children.GetLowerBound(0); c <= Tree.Children.GetUpperBound(0); c++) { CodeStatement[] cs = GenerateStatements(Tree.Children[c]); for( int i = cs.GetLowerBound(0); i <= cs.GetUpperBound(0); i++) { mCodeStatements.Add(cs[i]); } } } } else { mCodeStatements.Add (new CodeSnippetExpression (((MethodInfo)Tree.Node).Name.ToString() + "()")); } CodeStatement[] cstatements = new CodeStatement[mCodeStatements.Count]; IEnumerator enumStatements = mCodeStatements.GetEnumerator(); int statement = 0; while(enumStatements.MoveNext()) { cstatements[statement] = (CodeStatement)enumStatements.Current; statement++; } return cstatements; }
Figure 11 BuildExecute
private CodeMemberMethod BuildExecute (ExpressionTree Tree) { // this is the fixed part of each execute method: CodeMemberMethod m = new CodeMemberMethod(); m.ReturnType = new CodeTypeReference(typeof(void)); m.Attributes = MemberAttributes.Public | MemberAttributes.Override; m.Name = "Execute"; CodeMethodReferenceExpression loopCheckMethod = new CodeMethodReferenceExpression(); loopCheckMethod.MethodName = "NotFinished"; CodeMethodInvokeExpression loopCheck = new CodeMethodInvokeExpression(loopCheckMethod, new CodeExpression[0]); CodeIterationStatement whileLoop = new CodeIterationStatement (new CodeSnippetStatement(""),loopCheck, new CodeSnippetStatement(""), GenerateStatements(Tree)); m.Statements.Add(whileLoop); return m; }
Generator Class—Compiling New Code and Executing It
CodeDOM is used to create and populate the CodeCompileUnit for the generation namespace. The final steps needed to process a generation are code generation, compilation, and execution of all the new ant instances. These are all performed at the conclusion of the Generator.NewGeneration method. First, a C# code file is generated, as shown in the following code:
// Create the generated .cs file CodeDomProvider provider = new CSharpCodeProvider(); // Obtain an ICodeGenerator from a CodeDomProvider class. ICodeGenerator gen = provider.CreateGenerator(); // Create a TextWriter to a StreamWriter to // an output file. IndentedTextWriter tw = new IndentedTextWriter(new StreamWriter( mGeneratedNamespaceName + ".cs", false), " "); // Generate source code using the code // generator. gen.GenerateCodeFromCompileUnit(mCompileUnit, tw, new CodeGeneratorOptions()); // Close the output file. tw.Close();
Then the code is compiled:
ICodeCompiler compiler = provider.CreateCompiler(); CompilerParameters cp = new CompilerParameters(); cp.GenerateInMemory = true; cp.GenerateExecutable = false; cp.ReferencedAssemblies.Add("CodeDom.exe"); cp.OutputAssembly = mGeneratedNamespaceName + ".dll"; CompilerResults cr = compiler.CompileAssemblyFromFile( cp, mGeneratedNamespaceName + ".cs");
I'll be generating lots of these code files, and each one will be an assembly that I'll load and execute. Finally, I'll use reflection again to find all the types in the new assembly, which is named "a". I'll invoke the Execute method on each and save its TerminationReport, as shown in Figure 13.
Figure 13 Save to TerminationReport
Type [] mytypes = a.GetTypes(); foreach(Type t in mytypes) { Ant a2 = (Ant)Activator.CreateInstance(t); // the ant will stop after 400 steps, or when // it has gathered its Food Goal a2.Init(ref grid, 400, FoodGoal); a2.Execute(); // when the Execute() method finishes, get its terminating exception // to save its results Ant.TerminationReport doneReport = a2.mConcludingReport; // remaining code to save exception internally.... }
Building and Running the Application
The download consists of a single Visual Studio® .NET 2003 solution called CodeDOM. While the application runs, generated code files and DLLs accumulate in the \bin directory, so it's important to clean this directory occasionally. When the application starts up, it loads the DefaultGrid.XML file to paint an initial trail in the panel. It looks for that in the directory where the executable is running. It is currently located in the \bin\debug directory. If the application is run from another directory, the DefaultGrid.XML file should be moved there. The application will only run one experiment at a time.
Working with a Complex Problem
I'll conclude with a simple example that demonstrates how useful the application can be to perform experiments. Start the application, press the Get Grid button, and open the code file (called AlternateGrid.xml in the download). The winding trail has 76 pieces of food, with many gaps of one or two spaces. Change the number of generations to 20 and click the Generate button. When execution completes, the generation summary will show a clear increase in average fitness. Select Generation 20, and then select its best ant. Since the Generator works off of a Random instance with a fixed seed, the best ant in this generation will have gathered 65 items of food in 400 steps. The grid in Figure 14 shows the trail that appears when the Replay All button is used for this ant. It's a meandering, weaving pattern that doesn't appear to be very intelligent, but because the trail winds through the grid it manages to gather most of the available food.
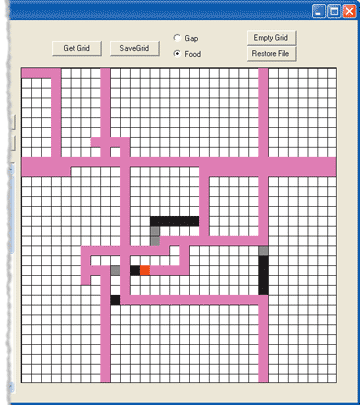
Figure 14** Inefficient Ant Trail **
Now let's add some intelligence to our base ant. Shut down the application, open the solution in Visual Studio, and find the code for the Ant class. There is a commented-out method called FacingGap. This method is just like FacingFood, but it allows the ant to see if there's a gap ahead, in addition to seeing if there is food ahead. You should uncomment the FacingGap method and rebuild the application.
Now do the same experiment that we just performed. Open AlternateGrid, select 20 Generations, and click the Generate button. Now the generator has an additional function available (FacingGap), and it will use this function as it generates the initial random ExpressionTrees. When the run is finished, find the best ant from Generation 20. Look at the code window and note its use of the FacingGap function. When the Replay All button is clicked, the trail in Figure 15 appears. The new function that was made available allowed the algorithm to generate an ant that will find all the food in close to the minimum number of steps.
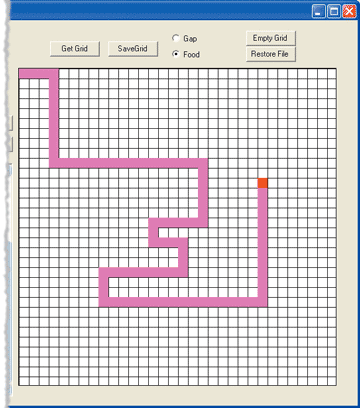
Figure 15** Trail of an Efficient Ant **
The analogy to nature here is the availability of a new gene. FacingGap is like a gene that makes the developed organism more sensitive to something in its environment—for example, an enhanced sense of smell. It is important to note that the algorithm employed this new "gene" with no knowledge of its meaning or usefulness. Its usefulness only became apparent when the organisms that included it manifested higher fitness than others.
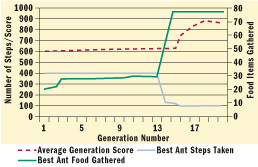
Figure 16** Plotting Generations **
When the program executes, it outputs a summary of each generation and its best ant to a file, LastRun.csv. Figure 16 shows the progress that the algorithm made in solving the last problem. Note the dramatic improvement in Generation 14, when an ant was discovered that gathered 76 items of food in 126 steps. The average score increased in the remaining generations because the progeny of that ant came to dominate the population, and further improvements lowered the required steps to 106. Figure 17 maps genetic programming terms to nature.
Figure 17 Genetic Programming in Nature
| Concept | Natural Evolution | GP Framework |
|---|---|---|
| Genotype—the genetic blueprint for an individual | DNA | Expression tree |
| Phenotype—an individual with their developed characteristics | Living organism | Generated ant |
| Natural Selection | The process by which the fittest individuals are "chosen" to survive and reproduce | Fitness function |
| Reproduction | Sexual reproduction | Crossover |
Further Work and Extensions
As stated before, the Generator class is not completely generic because it uses some internal knowledge about the TerminationReport class. This can be easily corrected by passing the TerminationReport as a class to the Generator constructor. It would be used in a manner similar to the way it uses the BaseClass type that is passed to it now.
This implementation of Artificial Ant is a simple one that was developed to show the potential for CodeDOM and reflection for genetic programming applications. It has a number of performance limitations that should be addressed in order to develop a useful, real-world problem solver. Fortunately, there is nothing in the architecture of .NET that would be an obstacle to high-performance genetic programming.
The first limitation is unnecessary code generation and execution. You'll probably recall that 10 percent of the ants in each generation are copied to the next generation. There is no reason to generate code and execute it for these ants—since they are unchanged, the generated code and behavior are unchanged as well.
The application generates a code file and then compiles the file. This is an anachronism from the development process because it was important to be able to see and debug code compilation during development of the code generation methods. It would be far more efficient to use the CompileAssemblyFromDOM method to build the assembly directly from the CodeCompileUnit.
Perhaps the single most important performance enhancement would be to implement one of the standard steps in GP processing. This step, called editing, takes expression trees and simplifies them. For example, functions with clauses like "Left; Right" can be removed because they just consume steps without changing the ant's state. In this sample application, the ant has only a single Boolean function, and many ants use deeply nested, completely redundant checks of this.
Editing and pruning code expressions would dramatically improve performance since the code fragments that must be manipulated would be far simpler. Editing has a practical benefit to the experimenter as well. Generated ants will be simpler, so it will be easier for an analyst to understand the problem-solving strategy they represent.
Brian Connolly is an independent consultant who specializes in transaction system design and performance analysis. He has led development teams that have produced international trading systems, data warehouses, and a major media Web site. Contact Brian at https://www.ideajungle.com.