Test Run
Group Determination In Software Testing
Dr. James McCaffrey
Code download available at:MSDN Code Gallery(153 KB)
Contents
Pure Plurality and Majority Runoff
Borda Count System
Condorcet Technique and Schulze Method
The Schulze Method in Code
More to Evaluate
Consider the general problem of determining a best option from a list of choices, where the decision-making process is performed by a group of people rather than by a single person or by a purely quantitative technique. Examples of this type of activity include the residents of a state voting for the state's governor from a list of candidates and the board of directors of a large company determining which of several smaller companies to target for acquisition. In essence, the group must rank its options in some way so that the best one can be determined.
Group determination of a best alternative occurs in software development and testing, too. For example, consider a group of beta users choosing the best user interface from a set of prototypes. Or imagine the members of an open source project voting for a policy.
I have observed that the practical techniques for performing group determination of a best alternative, and the potential pitfalls of the process, are not widely known in the software testing community. There are dozens of group analysis techniques. In this month's column I describe five of the most common methods used for group determination of a best alternative in a software testing environment: the pure plurality technique, the majority runoff technique, the Borda count system, the Condorcet method, and the Schulze method.
All of these analysis techniques are well-known outside of software engineering and have been extensively researched. I describe each technique with an emphasis on its application to software testing. I think you'll find knowledge of group analysis techniques a valuable addition to your toolkit.
Situations where exactly one of a set of alternatives must be selected by a group of people occur in a wide range of problem domains. Different problem domains tend to use different terminology. In sociology, for example, the study of this type of problem is usually called social choice theory and typically uses terms such as options and evaluators. In political science, analysis of these problems is often called voting theory and uses the terms candidates and voters. In mathematics, group determination of a best alternative is frequently considered a sub-branch of decision theory. I will use a mixture of terminologies in my discussion because there is no specific terminology set used when these techniques are applied to a software development and testing environment.
The techniques I describe in this column apply to a fairly narrow range of problems and do not apply strictly to quantitative scenarios where a best choice is clearly defined. As you'll see, when a group of people select a "best" alternative, the meaning of best is defined by the technique used. Also, the techniques I describe here do not apply to collaboration scenarios where a group of people use discussion and negotiation to arrive at a consensus decision.
Pure Plurality and Majority Runoff
Let's begin the discussion of group determination of a best alternative with a look at the simplest and most common technique—but let me warn you that this is not the best approach in many testing situations. Suppose you are developing an enterprise software application for your company's internal use and you create four quite different user interface prototypes. Although you could ask a single person to evaluate the different prototypes, in many cases a better approach is to ask a group of people to rank the four different designs.
It turns out that the process of performing a group evaluation and interpreting the results is somewhat trickier than you might expect. The simplest possible group evaluation technique is to submit the choices to the evaluators and allow them to choose, or vote for, just one alternative. The alternative that receives the most votes is declared the winner. This technique is often called the pure plurality rule.
So, suppose you submit your four different prototypes (let's call them A, B, C, and D) to 10 evaluators and ask each person to choose the best prototype. And suppose the results are: Prototype A is best according to 4 people, prototype B is ranked best by 3 people, prototype C is chosen by 2 people, and prototype D is selected best by 1 person. Therefore, you select prototype A for further development.
There are several problems with this. Suppose that while your evaluators are looking at your four prototypes, they either implicitly or explicitly rank each choice, as shown in Figure 1 . In this diagram, each column represents one evaluator's ranking of the prototypes.

Figure 1 Prototype Rankings for 10 Evaluators (Click the image for a larger view)
Notice that although prototype A is selected by the pure plurality rule, that prototype is evaluated as the worst by 60% of the evaluation group. Additionally, in this situation, suppose prototype A was compared in turn against each of the other prototypes. Prototype A would lose each head-to-head comparison by a 60% to 40% margin. A second, closely related problem with the pure plurality technique is that in some sense the non-winning opinions do not contribute directly to the final result.
The problems with pure plurality lead to another group selection technique usually called the majority runoff system. There are several variations on the technique, but the winner is required to gain more than 50% of the first-place votes of all votes cast.
This can be accomplished by having multiple rounds of voting or performing just a single round of voting but requiring the evaluators to rank all options. For example, if evaluators vote for the best prototype design according to the data in Figure 1 , no prototype would have a majority after the first round of voting. So the list of candidates could be reduced, usually to the top two options; in this case, prototype A with four votes and prototype B with three votes.
A second round of voting then takes place. If at that time evaluators vote according to the ranking preferences in Figure 1 , after the second round of voting prototype A would still receive four votes as best, but prototype B would receive six votes because the evaluators who originally selected prototypes C and D would now select prototype B.
In my experience, using multiple rounds of voting in a software development and testing environment has significant disadvantages compared to using a single round. For one thing, in some software development scenarios, multiple rounds of voting simply aren't feasible. Additionally, because it entails dealing with human beings, multiple rounds of voting can get tedious. Worse, situations can arise where a group of people are voting for losing alternatives over and over (receiving negative feedback each time) until they are forced to choose an option they don't really like. If the voters are stakeholders in the sense that they will be affected by the outcome of the voting, you may end up with disenfranchised voters at the end of a physical runoff scheme.
Instead of performing multiple actual rounds of voting where each evaluator votes for just one alternative, you can simply perform one round of voting but require evaluators to rank all candidates from best to worst. This allows you to determine voters' preferences in virtual rounds of voting.
Requiring ranking of all choices has certain disadvantages, too. The technique often isn't practical when the number of options is large (typically more than eight), simply because humans have difficulty comparing large numbers of alternatives. Also, research has shown that evaluators tend to get careless with their evaluations of options that are low on their list of preferences. And, when performing multiple physical rounds of voting, evaluators may not rank a subset of alternatives in the same order in which they rank the entire set of alternatives.
Schulze Method: Pros and Cons
The Schulze method has strengths and weaknesses. One weakness in some scenarios is that Schulze is far from intuitive. In situations where evaluators are stakeholders, the Schulze method can easily be viewed as a mysterious black box technique that produces a magic result.
The primary advantage of the Schulze method is that it has been extensively analyzed and has been shown to meet many favorable criteria. (Recall that the Borda count system can be affected by the removal of an irrelevant alternative.)
There are many voting-system criteria. For example, the monotonicity criterion can be loosely stated as the principle that a winning option cannot become a non-winner by one or more evaluators ranking that option higher. The independence of clones alternatives criterion is, stated loosely, that adding a new option that is identical to an existing option should not change the outcome of an analysis. There are many proposed voting-system criteria, and the Schulze method has been shown to meet most of these criteria as well.
An interesting exception is that the Schulze method violates what is called the participation criterion. In informal terms, it is possible to add to an existing system, new voters who prefer the current winner to some other alternative, which results in the less-preferred alternative becoming a Schulze winner.
In spite of its shortcomings, the Schulze method is often very effective, especially in situations with a large, educated group of evaluators (meaning they have knowledge of the underlying Schulze method) who are determining a policy alternative (as opposed to a product decision) and who are stakeholders in the final result. For example, the Schulze method is used by several open source groups to determine general policy decisions and to elect officers. In software testing scenarios, the Schulze method is generally the first technique I will choose to employ, and then I will use those results as a baseline against the results of other techniques.
Borda Count System
The problems with the pure plurality and majority runoff techniques led to the development of two group analysis techniques that are very common. These techniques, the Borda count system and the Condorcet pair-wise comparison method, are named after the two mathematicians who proposed the approaches in the late 1700s.
The Borda count approach is very simple and one with which you are almost certainly familiar. Suppose there are n alternatives. Each evaluator ranks the alternatives from best to worst. A top-ranked alternative is assigned a value of n-1 points, a second-ranked alternative is assigned n-2 points, and so on, down to the last-ranked alternative, which receives 0 points. The Borda count is just the sum of the point values for each alternative.
A quick example will make the ideas clear. Suppose there are four choices, A, B, C, and D. In this case, a first-place ranking is worth 3 points, second place is worth 2, third place is worth 1, and last place is worth 0 points. Figure 2 shows the results and then, underneath, the Borda counts for seven evaluators where alternative A is selected as the best option.

Figure 2 Results and Borda Counts for Seven Evaluators (Click the image for a larger view)
The Borda count technique is widely used in many problem domains, especially in sports competitions. Advantages of the Borda count technique when used in a software development and testing environment are that the technique seems to make sense intuitively, and all evaluators' opinions are taken into account.
The Borda count system has several technical problems, however. Suppose that we decide to remove option D, which was a clear loser. Common sense suggests that removing an irrelevant alternative should not affect the final result. But Figure 3 shows what happens after removing option D. Now option B becomes the best alternative instead of option A. In other words, with this set of data, removing an irrelevant alternative changes the outcome. It is even possible to construct Borda count examples where the best alternative actually becomes the worst alternative. This effect is sometimes called the Borda count winner-becomes-loser paradox.
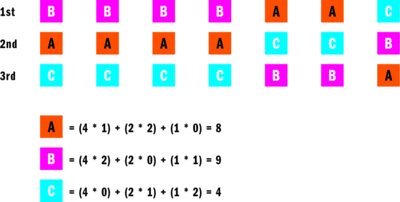
Figure 3 Results and Borda Counts after Removing Option D (Click the image for a larger view)
There are two other closely related technical problems with the Borda count technique. The first is the pair-wise comparison problem. It is possible when using the Borda count technique to run into situations where the Borda winner would lose against every alternative in a head-to-head comparison.
Suppose, for example, that there are four alternatives and 12 evaluators (see Figure 4 ). Using the Borda count method, alternative A is selected as best with 25 points. However, if we look at head-to-head comparisons we notice that alternative B is preferred to all other alternatives: B is preferred to A by a score of 7 people to 5, B is preferred to C also by 7 to 5, and B is preferred to D again by 7 to 5.
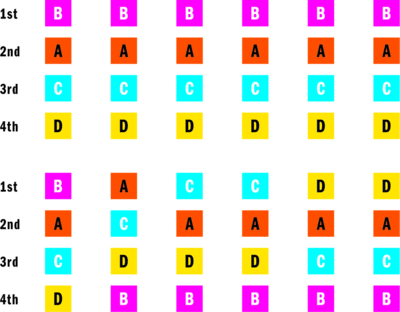
Figure 4 Option B Is the Head-to-Head Winner (Click the image for a larger view)
Another problem with the Borda count technique is that it is vulnerable to evaluator manipulation. It is theoretically possible to affect the outcome of a Borda count evaluation by adding a spurious alternative that is very close (in terms of evaluators' preferences) to an existing alternative. This can have the effect of diluting close alternatives and changing the winner of the analysis. The references at the end of this column contain examples of the effect.
Despite the Borda count technique's technical flaws, the system is quite practical and often works well for policy determination by small groups in a software testing environment. Based on my experience, the Borda count technique is generally seen by voters as fair in a subjective way, and, therefore, if voters are stakeholders, the people who voted for non-winning alternatives generally accept the result of the voting and do not come away with a psychological bias against the winning alternative.
The moral of the story here is that if you do use the Borda count technique, be alert for, and check your data for, the effect of removing an irrelevant alternative, the result of pair-wise comparisons between the Borda count winner and non-winning alternatives, and the mid-process addition of a new alternative.
Condorcet Technique and Schulze Method
The Condorcet technique for collaboratively determining the best option from a set of choices was developed primarily as a reaction to the head-to-head paring problem of the Borda count method. The Condorcet method is very simple. It requires evaluators to rank all alternatives, and then a comparison of the results between each possible pair of alternatives is performed.
If one alternative beats every other alternative in a head-to-head comparison, then that one alternative is declared the Condorcet winner. If there is no Condorcet winner, then a separate, tie-breaking technique is employed. The tie-breaking technique can be any other technique; the point of the Condorcet system is that a unanimous head-to-head winner should automatically win over any alternatives chosen by any other criteria.
In practice, the Condorcet system is not often used by itself as a group evaluation technique. Instead, evaluation techniques such as pure plurality and Borda count are mathematically analyzed to see if they satisfy the Condorcet principle in all cases. So, instead of reading something like, "We decided to use the Condorcet system to evaluate our alternatives," it is more usual to read something like, "We decided to use the XYZ evaluation system, which satisfies the Condorcet principle."
One of the most interesting systems that satisfies the Condorcet principle has a variety of names, including the Schulze method, the clone-proof Schwartz sequential dropping technique, and the beat-path method. I will call this technique the Schulze method.
The Schulze method is somewhat more complicated than the other techniques I've described so far. It is similar to the Condorcet system in the sense that Schulze looks to see if one option dominates all other options. However, instead of directly using raw ranking data, as the Condorcet system does, the Schulze method performs a head-to-head comparison using an indirect measure of the strength between alternatives. This indirect measure is called the path strength.
Let's walk through an example. Take a look at Figure 5 . It shows a simple demo of the Schulze method in action. The first part shows the example input. There are four options (A, B, C, and D) and 11 evaluators. The first line means that 3 evaluators rank option A better than B, which in turn is better than C, which is better than D. The Schulze method allows evaluators to rank options equal to each other and also allows evaluators to leave out alternatives altogether.
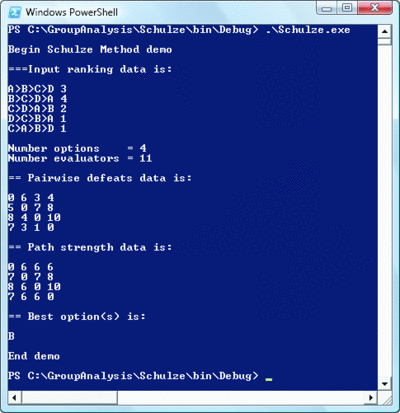
Figure 5 Schulze Method Demonstration (Click the image for a larger view)
The next part of the output shows a matrix of pair-wise defeats. This defeats matrix is computed directly from the original ranking data.
The first row of the matrix means option A is preferred by 6 voters over option B, preferred by 3 voters over option C, and by 4 voters over option D. The second row of the matrix means option B is preferred by 5 voters over option A, by 7 voters over option C, and by 8 voters over option D. The third and fourth rows, for options C and D, respectively, are interpreted similarly. The pair-wise defeats matrix has 0 values on the main diagonal because these values are comparisons between an option and itself.
At this point the Condorcet system would check this direct pair-wise data to see if there is a unanimous head-to-head winner, but the Schulze method derives an indirect measure of strength between alternatives. The next part of output is the strength of paths between each option. This is the key idea behind the Schulze method and is a very clever notion. The third row of this matrix means the strength of the path from option C to option A is 8, the strength from C to B is 4, and the strength from C to D is 10.
Explaining the idea of path strength is best done visually, as shown in Figure 6 . First we express the raw ranking data as a matrix of pair-wise defeats. Next we can conceptualize the pair-wise defeats data as a directed graph.
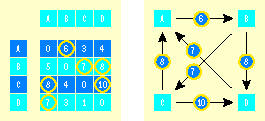
Figure 6 Pair-Wise Defeat Data in Matrix and Graph Forms (Click the image for a larger view)
The arrow from node A to node B means that option A is preferred by 6 evaluators over option B. I do not put an arrow from node B to node A because option B is preferred by only 5 evaluators over option A, so A dominates B. In this example, all the arrows are unidirectional, but if two nodes are preferred by equal numbers of evaluators, then I can draw a bidirectional arrow.
Now consider the path between node A and node D. A beats B by 6, and B in turn beats D by 8. We chose 6, the smaller of these two values, to represent the overall strength of path between A and B. The idea is that the overall strength between two nodes that have intermediate nodes is best represented by the smallest direct node-to-node strength. Notice that we can also take a different path from A to D and say that A beats B by 6, and B beats C by 7, and C beats D by 10, and select the smallest number, 6, which would give the same result.
It turns out that computing the strength of each pair of nodes can be performed by a variation of the elegant Floyd–Warshall algorithm, as I'll explain in a moment. The standard Floyd–Warshall algorithm finds the shortest paths in a weighted, directed graph. Once the path strengths have been determined, we can determine the Schulze method winners by checking to see if there is any option where its path strength is greater than or equal to all other options' corresponding path strengths.
Figure 7 shows the matrix of path strengths that corresponds to the data in Figure 6 and demonstrates that option B is a Schulze method winner. Visually, an option is a Schulze winner if every path strength value on that option's row is greater than or equal to the corresponding value across the matrix's main diagonal.
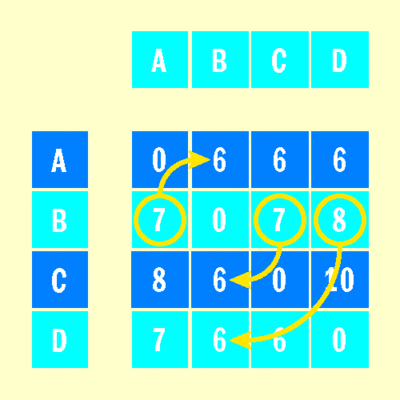
Figure 7 Path Strength Data Used to Determine a Schulze Winner
Option B is the winner because option B's path strength to option A is 7 (but option A's path strength to B is just 6), option B's path strength to option C is 7 (but C's path strength to B is just 6), and option B's path strength to option D is 8 (but D's path strength to B is just 6). On the other hand, option D is not a Schulze winner because option D's path strength is better than option A (7 to 6), but option D's strength is worse than option C (6 to 10).
The Schulze Method in Code
In this example there is just one Schulze winner, but it is possible for there to be multiple Schulze winners. In situations like these you would have to use some form of tiebreaker. Let's go over some of the code in the program that generates the output in Figure 5 to help explain the Schulze method.
The program begins by setting up an enumeration type to represent the alternatives and a global value N to hold the actual number of alternatives:
enum options { A, B, C, D, E, F, G, H, I, J };
static int N; // actual number of options
Then the demo program sets up problem input as a string array:
string[] rawData = new string[] {
"A>B>C>D 3",
"B>C>D>A 4",
"C>D>A>B 2",
"D>C>B>A 1",
"C>A>B>D 1"
};
For simplicity, my demo program assumes that ties are not allowed and that all options are ranked. Doing so lets me parse the raw data strings very easily. The complete demo program is available in the code download that accompanies this column. You should be able to modify the code to allow ties and missing options, without too much trouble.
Next, my demo program scans through the rawData string array and determines and prints the number of options and the number of evaluators. Then the programs rescans the input array and creates a matrix of pair-wise defeats data using a static helper method named MakeDefeats:
int[,] defeats = MakeDefeats(rawData);
Console.WriteLine("\n== Pairwise defeats data is: \n");
Print(defeats);
The defeats matrix is then passed as input to another helper method, named MakePathStrengths, which creates a matrix of path strengths:
int[,] strengths = MakePathStrengths(defeats);
Console.WriteLine("\n== Path strength data is: \n");
Print(strengths);
Inside the MakePathStrengths method, I begin by eliminating entries that are dominated:
int[,] result = new int[N, N];
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
if (d[i, j] > d[j, i])
result[i, j] = d[i, j];
else
result[i, j] = 0;
}
}
Notice that the statement result[i, j] = 0; is not technically necessary because C# automatically initializes int arrays to all 0 values.
Next I use a variation of the Floyd–Warshall algorithm to compute the strength of each possible path:
for (int k = 0; k < N; ++k) {
for (int i = 0; i < N; ++i) {
if (k == i) continue;
for (int j = 0; j < N; ++j) {
if (k == j || i == j) continue;
result[i, j] =
Math.Max(result[i, j], Math.Min(result[i, k], result[k, j]));
} //j
} //i
} //k
If you go ahead and hand-trace through this code, you will see how it implements the determination of the path strength that exists between node [i] and node [j], as I described previously. The Max method in the code works to ensure that on each iteration through the outer loop I update the result matrix only if a stronger path happens to be found. The Min method in the code corresponds to the idea of using the smallest direct node-to-node strength to represent the overall path strength that is in existence between any two nodes.
After I have all the path strengths, I can use that information to compute an array that represents Schulze winners and then iterate through that array and display the enumeration value that corresponds to each winner:
>bool[] winners = MakeWinners(strengths);
Console.WriteLine("\n== Best option(s) is: \n");
for (int i = 0; i < winners.Length; ++i) {
if (winners[i] == true)
Console.Write(Enum.GetName(typeof(options), i) + " ");
}
The MakeWinners method sets up a one-dimensional Boolean array where a value of true indicates a winner and a value of false indicates a non-winner. I assume every option is a winner, then iterate through the path strength matrix, comparing the strength value at index [i,j] with that at index[j,i] to see if that option is in fact a non-winner:
static int[] MakeWinners(int[,] ps) {
bool[] result = new bool[N];
for (int i = 0; i < N; ++i)
result[i] = true;
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j)
if (ps[i, j] < ps[j, i])
result[i] = false;
}
return result;
}
More to Evaluate
Some of the key factors you should consider when using group evaluation techniques include the number of alternatives, the number of evaluators, whether the alternatives are policy decisions or product decisions, and the extent to which evaluators are affected by the final result of the analysis. In general, you should use more than one group analysis technique when possible in order to use multiple results to cross-validate your analysis (if multiple techniques yield the same conclusion, you gain some measure of confidence in your results).
The situations where the techniques I've described in this column are used are almost always quite subjective. Your experience and intuition must play a big part in analyzing group determination results.
As a general rule of thumb, the pure plurality technique is only effective in situations where evaluators are not stakeholders or when ranking all alternatives is not feasible. The majority runoff technique has the potential to alienate up to 49% of your evaluators, and based on my experience you should generally use this technique primarily to supplement other techniques.
The Borda count system, in spite of technical flaws, works quite well, especially when the evaluators are stakeholders in the analysis. The Condorcet principle is very simple and so can often be used to validate the results of other techniques. The Schulze method is an excellent general-purpose technique in many software testing situations, except when you are dealing with a relatively small group of evaluators who are influenced by the results and who do not understand the Schulze algorithm.
This column just scratches the surface of an interesting and useful subject. There is a large body of research on group techniques to determine the best alternative from a set of options. One good reference is the book A Primer in Social Choice Theory, by Wulf Gaertner (Oxford University Press, 2006). I also recommend Comparing Voting Systems, by Hannu Nurmi (Springer-Verlag, 1987).
You might find it interesting to compare the problem of group analysis to determine a best alternative to the related problem of rating a set of alternatives based on multiple attributes. If that's the case, I address two different multi-attribute decision techniques in the June 2005 ( msdn.microsoft.com/magazine/cc163785 ) and October 2006 ( msdn.microsoft.com/magazine/cc300812 ) installments of the Test Run column.
Send your questions and comments for James to testrun@microsoft.com .
Dr. James McCaffrey works for Volt Information Sciences, Inc., where he manages technical training for software engineers working for Microsoft in Redmond. He has worked on several Microsoft products including Internet Explorer and MSN Search. James is the author of .NET Test Automation Recipes (Apress, 2006), and he can be reached at jmccaffrey@volt.com or v-jammc@microsoft.com .