January 2009
Volume 24 Number 01
Test Run: Analyzing Project Exposure and Risk Using PERIL
By Dr. James McCaffrey | January 2009
Contents
Meta-Risks
Risk Identification
Risk Analysis
Wrapping Up
All software projects face risks. A risk is an event, which may or may not occur and which causes some sort of loss. The relationship between risk and software testing is straightforward. Because, except in rare situations, you cannot exhaustively test a software system, risk analysis reveals issues that can cause the most loss. You can use this information to help prioritize your testing effort. In this month's column, I present practical techniques you can use to identify and analyze the risks involved with a software project. Let's begin.
Imagine a hypothetical situation in which you are developing an ASP.NET Web-based application of some sort. Figure 1 illustrates some of the key ideas and problems associated with software risk analysis. The overall process of risk analysis involves identifying your risks, estimating how likely each risk is, determining the loss associated with each risk, and combining likelihood and loss information into a value called risk exposure.
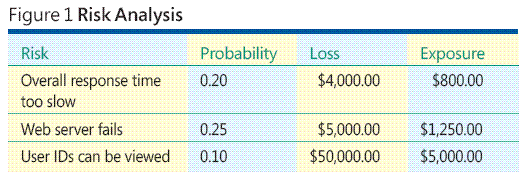
According to the example data in Figure 1, the risk that "User IDs can be viewed" has the highest exposure, so other factors being equal, you would likely want to make it a top priority to test for this to prevent the risk from becoming a reality. But how can you identify risks? How can you estimate risk probability and loss? Can you still perform risk analysis if you cannot estimate risk probability and loss?
Although there have been several efforts to formalize and standardize risk analysis terminology, in practice different terms tend to be used in different problem domains. I will use the term "risk analysis" to mean computing risk exposure by multiplying the risk probability or likelihood by the risk loss, or to mean the overall process of identifying, analyzing, and managing software project risk.
In spite of the fact that risk analysis is a critically important part of software development, based on my experience, many risk analysis techniques are not widely known in the software testing community. If you search the Web, you will find tens of thousands of references on software risk analysis. However, the majority of these references either address risk analysis at a very high level and do not present practical techniques or present just one specific risk analysis technique and do not explain how the technique fits into an overall risk analysis framework. I'll present you with both an overview of risk analysis and useful techniques you can employ immediately in your software development environment.
In the sections of this column, I describe two meta-risks that are common to all software projects. Then I present three ways you can identify specific risks associated with your software project and three ways to analyze risk. In particular, I will introduce you to an interesting new risk analysis technique called Project Exposure using Ranked Impact and Likelihood (PERIL) that is especially useful in a software development environment. I conclude with a brief discussion of risk management. I believe that the techniques presented here will become an extremely valuable addition to your software testing, development, and management tool kit.
Meta-Risks
Two special types of software project risk analyses are what I call time and cost meta-risk analyses. Traditional project management defines a concept which has different names including "the project management triple constraint" and "the project management triangle." The idea is, in short, that virtually every project has three limiting factors: cost, schedule, and scope. Cost is how much money you have to spend on the project, schedule is how long you have to complete the project, and scope is the set of required project features and their quality.
The three project constraints have a variety of aliases. For example, cost is also referred to as budget or money. Schedule is often called time or duration. And scope is sometimes called features, or quality, or even features/quality. Notice that this last features/quality constraint can be (and often is, in fact) considered to be two distinct constraints.
A key notion is that a change in any one of the constraints will likely cause a change in one or both of the other two constraints. For example, if you are developing a software application, and you are suddenly required to finish the project in a shorter amount of time than originally planned, you probably will have to spend more money (for example, to buy additional resources or outsource part of the project) or cut some features or quality. If the budget for your project is cut, then you will likely have to extend the time to finish the project, remove some features, or lower the quality of your project. Using the project management triangle paradigm, because software testing is designed to improve the quality of a system, it follows that the two highest levels of risk in a software project are that the project does not finish on time and that the project runs over budget.
There is a relatively simple but effective way to estimate the overall schedule and cost risks to a software project. Let's look just at the time/schedule meta-risk (analyzing budget/cost risk works in exactly the same way). The first step in a high-level meta-risk analysis is to break your overall project into smaller, more manageable chunks of activities.
For example, suppose you are working on a small Web application project, and the project must be completed in 30 working days. You begin the meta-risk analysis by listing all the activities involved in the project. The most common approach here is to create what is called a work breakdown structure (WBS), which you can see in Figure 2. You create a top-level task that consists of the entire project. Then you break that task into a number of smaller sub-tasks, typically about three to seven tasks. You repeat the process, decomposing each sub-task into smaller sub-tasks until you reach the appropriate level of granularity for your environment.
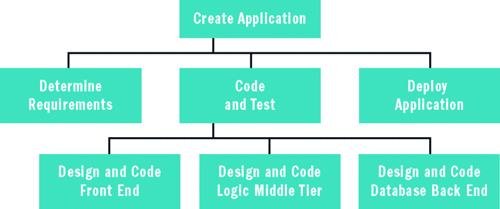
Figure 2 Work Breakdown Structure
The bottom level, leaf node tasks are sometimes called work packages. Exactly how you decompose your tasks and how granular you make your WBS depends on a number of factors. For example, in an agile development environment, you may well decide that a simple two-level deep work breakdown structure meets your needs. Or, if you are working on a very large, complex software project using a traditional software development lifecycle methodology, you may have tens of thousands of work packages.
You can create a small WBS by hand, use generic productivity tools such as Microsoft Office Excel, or use sophisticated tools such as Microsoft Office Project. A WBS does not contain sequencing, time, or cost information. In other words, a WBS tells you what must be done, but not in what order, and does not tell you how long each task will take or how much each will cost. After you create your work breakdown structure, typically the next step is to use the work packages to create what is called a precedence diagram.
.gif)
Figure 3 Precedence Diagram
The precedence diagram adds sequencing information. The diagram shown in Figure 3 indicates that the Requirements task must be completed before the Database Back End task, which in turn must be completed before both the Middle-Tier task and the Front-End task can begin. These last two tasks can be performed in parallel according to the precedence diagram. Finally, both the Middle-Tier task and the Front-End task must be completed before the Deploy Application task can begin.
After creating a precedence diagram with its sequencing information, the next step in a time meta-risk analysis is to estimate the time required for each individual work package. Although you can estimate each time as a single data point, a better approach is to supply three estimates—an optimistic estimate, a best-guess estimate, and a pessimistic estimate.
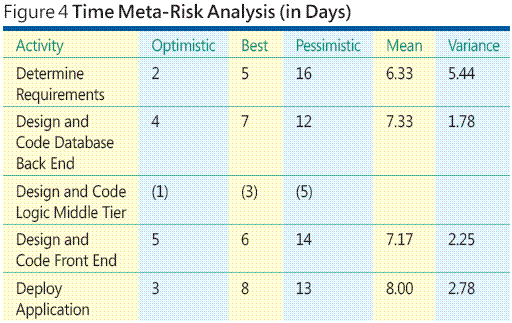
OK, but just where do such estimates come from? Determining time and cost estimates is by far the most difficult part of software project meta-risk analyses. There are many ways to estimate activity time and cost. You can use historical experience, educated guesses, sophisticated math models, and so on. The techniques you use will depend upon your particular situation. Regardless of the method you use, estimating the time and cost of a set of smaller activities is much easier than estimating the time and cost of one monolithic activity. The table in Figure 4 shows an example time risk meta-analysis.
When you are analyzing optimistic, best-guess, and pessimistic time data, you usually use a simple mathematical distribution called the Beta distribution. The mean, or average, of a Beta distribution is computed as this:
(optimistic + (4 * best-guess) + pessimistic) / 6
So for the Deploy Application task, the mean estimated time for completion is:
mean = (3 + 4*8 + 13) / 6 = 48 / 6 = 8.0 days.
Notice that a Beta mean is just a weighted average with weights 1, 4, and 1. Therefore, the variance of a Beta distribution is given by this formula:
((pessimistic - optimistic)/6)²
So for the Deploy Application task the variance is:
variance = ((13 - 3) / 6)² = (10/6)² = (1.6667)² = 2.78 days²
The overall standard deviation for the project is the square root of the sum of the activity variances. Thus, in this example, the equation looks like the following:
std. deviation = sqrt(5.44 + 1.78 + 2.25 + 2.78) = sqrt(12.25) = 3.50 days
Notice that my calculations do not use the data for the Design and Code Logic Middle-Tier activity. Because the Logic Middle-Tier activity can be performed in parallel with the Database Back-End activity, and the Front-End activity cannot begin until both parallel activities have finished, the shorter parallel activity (Logic Middle-Tier) does not explicitly contribute to the overall time to complete the project.
This type of analysis is called the critical path method (CPM) and is a standard project management technique. With the schedule mean and variance data computed, you can now compute the probability that the entire project will take longer than 30 days to complete:
z = (30.00 - 28.83) / 3.50 = 0.33 p(0.33) = 0.6293 p(late) = 1.0000 - 0.6293 = 0.3707
First, you compute the so-called z-value, which is equal to the amount of time you have scheduled to finish the project (in this case, 30 days) minus the estimated time to completion (28.83 days), divided by the total task standard deviation (3.50 days). Then you take the z-value (0.33) and look up the corresponding p-value in a Standard Normal Distribution table or use the Excel NORMSDIST function (0.6293). Finally, you subtract the p-value from 1.0000 to get the probability that your project will go over schedule.
You are performing a one-tail analysis here because you only care if you take longer than scheduled and don't care if you take less time. With this example data, the probability that the Web application takes longer than 30 days to complete is 0.3707, or nearly 40%—a rather risky situation. If you think about it for a moment, this result should make sense. Your planned schedule of 26 days of development is too close to the project limit of 30 days and so you may not have enough wiggle room to account for schedule variances.
Obviously, your meta-risk results are only as good as your input data—your time estimates in this case. If your input estimates are wrong, then no amount of statistical analysis can produce meaningful results. You can compute the meta-risk probability that your project will go over budget using the same technique as I've just demonstrated for schedule. Once you have the probability that your project will go over schedule, you can compute the risk exposure for the meta-risk if you can estimate the monetary loss due to being late.
In some situations, you may be under a contract to create a software system, and the contract may have well-defined and significant late penalties. For example, suppose your contract states that there is a $10,000.00 penalty for late delivery. Your meta-risk exposure is $10,000.00 * 0.3707 = $3,707. In other cases, the cost of a late software project is too difficult to estimate beyond "very, very expensive."
But notice that even without computing a risk exposure, your time meta-risk analysis yields useful information. If you examine the data in Figure 4, you can see that Determine Requirements task has the greatest schedule variance. Therefore, simply applying additional resources early on in the project can reduce your task variance, which in turn will reduce the probability of going over schedule.
Risk Identification
Unlike time and cost meta-risks, where the risk events can be determined in a somewhat step-by-step (although by no means easy) way by iteratively decomposing tasks into smaller subtasks, risk identification in the general case is much less mechanical. In a software development and testing environment, there are three main approaches to risk identification: taxonomy-based, scenario-based, and specification-based.
A taxonomy is just a classification list. Consider the following analogy. You are going to take a trip on an airplane, so you use a standard reminder list that you use before every trip. The list contains statements or questions such as, "Do I have my ID?" and "Have I checked to see if my flight is on time?"
Over the years, many people and organizations have created software risk taxonomies. One such list was created by Barry Boehm, an early pioneer and a well-known researcher in the area of software project risk. In 1989 Boehm identified a top 10 software risk taxonomy, and he updated the list in 1995. The 1995 version of the top 10 software project risk taxonomy is listed here:
- Personnel shortfalls
- Schedules, budgets, process
- Commercial off-the-shelf software, external components
- Requirements mismatch
- User interface mismatch
- Architecture, performance, quality
- Requirements changes
- Legacy software
- Externally performed tasks
- Straining computer science
It should be apparent to you that Boehm's top 10 risk list does not immediately identify risks. Rather, the taxonomy merely provides you with a starting point to begin thinking about risks that apply to your software project. For example, the first risk, "Personnel shortfalls," encompasses have many different possible risks related to staffing. Your project simply may not have enough engineers to create your application or system. Or a key engineer may leave the project halfway through the project's schedule. Or the engineering staff may not have the technical skills needed for the project. And so on.
Most of the top 10 risk categories should be familiar to you, except for perhaps the 10th risk category, "straining computer science." This is somewhat of a catch-all category and covers tasks related to things such as technical analysis, cost-benefit analysis, and prototyping.
Another commonly used software risk taxonomy list was created by the Software Engineering Institute (SEI). The SEI is one of 36 federally funded research and development centers in the U.S. These research centers are rather strange hybrid organizations which are funded by public money, but sell products and services. The SEI software risk taxonomy was created in 1993 and consists of approximately 200 questions. For example, question #1 is, "Are the requirements stable? If no, what is the effect on the system (quality, functionality, schedule, integration, design, testing)?" Question #16 is, "How do you determine the feasibility of algorithms and designs (prototyping, modeling, analysis, simulation)?" You can find the SEI risk taxonomy in an appendix to the document.
In scenario-based software risk identification, you imagine yourself in different roles, create scenarios for those roles, and identify what could go wrong in each scenario. Using the airplane trip analogy I described previously, you might mentally trace the steps you will be taking on your trip. For example, "First I drive to the airport. Then I park my car. Next, I check in at the airline counter." This scenario process could reveal many risks including traffic delays due to road construction or an accident, parking unavailability, forgetting your ID, and so on.
In a software project environment, some common roles used for scenario-based risk identification are users, developers, testers, sales people, software architects, and project managers. A user scenario might be something along the lines of, "First, I install the application. Next, I launch the application." In many cases a risk identification scenario maps directly to a test case.
Scenario-based risk identification roles are not necessarily people. Roles can be software modules or subsystems too. For example, suppose you have some C# object that performs encryption and decryption. You can imagine that the object is the role and create scenarios such as, "First I accept some input and instantiate myself. Next I accept some input and pass it to my encrypt method." There has been less research on scenario-based software risk identification than on taxonomy-based identification. The research paper found at Risk Identification Patterns for Software Projects presents a good overview of the field and proposes an interesting, theoretical, pattern-based approach to risk identification.
In addition to taxonomy-based and scenario-based risk identification strategies, a third approach is a specification-based strategy. In this approach you closely examine each feature and process in your product or system specification documents and attempt to identify what can go wrong. Using the airplane trip analogy, you might carefully examine a detailed trip itinerary which was created by a travel agent. Imagine that one of your specification documents for a Web application states that you intend to use an outside contractor to produce the various Help files for the application. An external project dependency can give rise to a long list of risks. What if the contractor fails to deliver on time? What if the contractor's work quality does not meet your subjective standards?
There is no single, optimal risk identification strategy, as each has pros and cons. Risk taxonomies are an excellent way to begin the process of identifying the risks in your software project. They provide a somewhat mechanical way to get started in the sense that you simply start examining each question or statement in the taxonomy. Taxonomies also help you to distribute the risk identification process among several people by assigning different people to different taxonomy questions. On the negative side, using taxonomies for risk identification can be very time consuming. Also, taxonomies are, by their nature, generic and so they cannot identify risks that are specific to your software system unless you put in the effort to discover these specific risks.
Compared to taxonomy-based risk identification, an advantage of a scenario-based approach is that it tends to be less generic and forces you from the beginning to be more definite. On the other hand, scenario-based risk identification is somewhat more art than science and you can easily miss a key scenario. Specification-based risk identification is usually the least generic, most specific approach. However, a specification-based approach will yield results only as good as your specification documents. When used together, the three approaches give you a good chance of accurately identifying your software risks.
Risk Analysis
Risk analysis is the process of combining the probability (or likelihood) of a risk event with the monetary loss (or negative effect) that occurs if the event happens, to produce a value that can be used to compare and prioritize the risk against other risks. In this section, I present two older approaches to risk analysis (the expected value technique and the categorical technique), and one new approach called PERIL. Let's look at the expected value technique first.
Take a look at the example shown in Figure 5. Suppose you have identified four risk events. Let's call them Risk A, Risk B, Risk C, and Risk D. You assign probabilities to each risk event. A probability is a number between 0.00 (meaning impossible) and 1.00 (meaning certainty) that indicates how likely the event is. Next, you assign a monetary loss value to each risk event, which is the cost to you if the risk event occurs. Now for each risk event you simply multiply the risk's probability and the risk's loss to get the risk exposure.
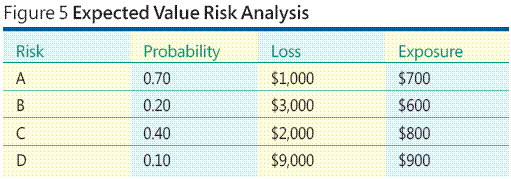
Using this method, risk exposure is just a form of expected value. Obviously, there are several major problems with the expected value approach. How can you estimate risk probabilities? How can you estimate a risk loss? In some situations you may have good historical data or experience to base your estimates upon, but this is generally a rare situation when creating software. Based on my experience, the expected value approach to risk analysis is often not feasible in a software development environment.
Because it is difficult or even impossible in many software development environments to estimate the probability of a risk event or its associated loss, a common alternative is to use categorical scales for both risk probability and risk loss. This is the categorical technique. An example will make the idea clear. Suppose you have identified four risks, A, B, C, and D. Now instead of guessing at a probability and a loss for each risk, you generate a categorical risk exposure table like the one shown in the top part of Figure 6.
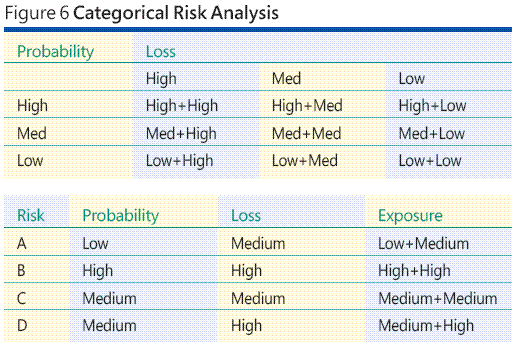
As you can see, I have a total of nine categories of risk exposure. There are three categories of risk probability—Low, Medium, and High. There are three categories of loss—also Low, Medium, and High. The cross product of probability category and loss category yields nine risk exposure categories, from Low-Low (low probability of a low loss) through High-High (high probability of high loss). Now I can look at each of my four risk events, assign a Low, Medium, or High probability, and then a Low, Medium, or High loss, to yield a nine-point risk exposure. The idea is that it is often more reasonable to assign a probability value of "Low" instead of an exact numeric value like 0.05 for example.
The hypothetical data in the table in the bottom part of Figure 6 suggest that Risk B has the highest exposure and may warrant more attention or resources (including testing) than Risk A, which has the lowest exposure. Although a categorical risk analysis approach somewhat eases the problem of assigning difficult or impossible-to-determine probabilities and loss information, the technique introduces new problems.
Notice that I arbitrarily use three categories for both probability and loss. This is a very coarse approach. But suppose I decide to improve my risk analysis by using five categories for both the probability factor and the loss factor: Very Low, Low, Medium, High, and Very High. Now I would end up with a total of 25 risk exposure categories—(Very Low + Very Low) through (Very High + Very High). How would I rank or compare these 25 exposure values? Just how does a (Very Low + High) risk exposure compare to a (High + Medium) exposure? If multiple people are evaluating your categorical risk exposure data, would they interpret the exposure data in the same way?
To address the problems with a purely categorical risk analysis approach, several years ago I developed a technique I call Project Exposure using Ranked Impact and Likelihood (PERIL). The essence of the idea is to use categories (as in the categorical approach) but convert them into a quantitative scale so they can be easily combined (as in the expected value approach) to produce numeric exposure metrics.
Let me show you an example. Suppose you have identified four risks: A, B, C, and D. Now suppose you decide that trying to assign meaningful numeric values to each risk's probability and loss is just not feasible. Additionally, you decide that in your particular environment it makes sense to categorize risk likelihood into five categories: Very Low, Low, Medium, High, and Very High. Next, you determine that you will categorize loss/impact on a four-point scale: Very Low, Low, High, and Very High. The PERIL technique maps categorical data onto a quantitative scale using a simple mathematical construct called rank order centroids. The mapping technique is best explained by example. For the five-category likelihood scale my five rank order centroid mappings are shown in Figure 7.
Similarly, my four-category impact mappings are computed, as shown in Figure 8. Now I can combine each risk's likelihood and impact centroid value to compute the risk's exposure by multiplying. For example, look at Figure 9. Here, Risk D has High likelihood, which maps to 0.25667, and Low impact, which maps to 0.14583, so the exposure is 0.25667 * 0.14583 = 0.03743. From this data I conclude the Risk C clearly has the highest exposure, and I would look at ways to prevent the risk from occurring and create a contingency plan if the risk event does occur.
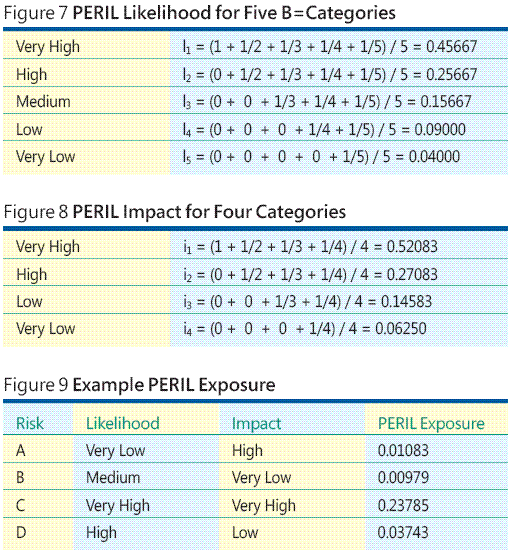
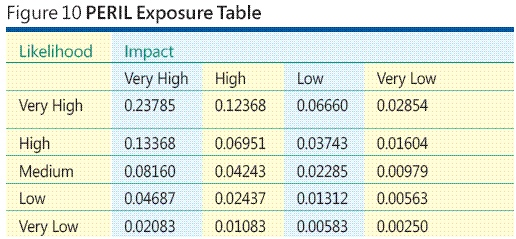
Instead of computing each risk's exposure individually, I can construct a complete PERIL exposure lookup table for five likelihood levels and four impact levels, and then simply read PERIL exposure values from the table, as illustrated in Figure 10. The PERIL technique generalizes to any number of likelihood and impact categories.
Rank order centroids map ranks (such as first, second, third) to numeric values (such as 0.61111, 0.27778, 0.11111). Notice that rank order centroid values are normalized in the sense that they sum to 1.0 (subject to rounding error). Expressed in sigma notation, if N is the number of categories then the numeric value corresponding to kth category is:
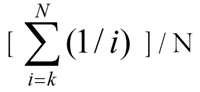
There are many other mathematical mappings between categories and numeric values, but there is some research which suggests that using rank order centroids is a very good way to map rankings such as the ones used in risk analysis. A complete discussion of rank order centroids is outside the scope of this column, but consider this informal argument. Suppose you are dealing with just two categories of risk event likelihood: High and Low. Presumably the High-risk event likelihood has a probability of occurring that is greater than 0.5 and therefore the Low-risk event likelihood has a probability of less than 0.5. Without any additional information, you can assume that the High event likelihood is halfway between 0.5 and 1.0 and so equals 0.75. In the same way, the Low event likelihood is halfway between 0.0 and 0.5 which is 0.25. These two values, 0.75 and 0.25, are rank order centroids for N = 2 categories (as shown in Figure 11).
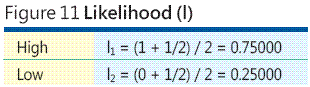
Notice that when using PERIL, I use the terms likelihood and impact rather than probability and loss. PERIL likelihood and impact are relative, normalized values. Even though PERIL likelihood values sum to 1.0 just as a probability set does, let me emphasize that PERIL likelihood values are not probabilities. Similarly, PERIL impact values have meaning only when compared with each other and are not monetary loss values.
The three techniques to determine risk exposure—the expected value technique, the categorical technique, and the PERIL technique—have strengths and weaknesses. If you have solid historical data that allows you to estimate the probabilities of risk events and the monetary loss associated with each event, then the expected value technique is usually the best approach. However, in a software development and testing environment you rarely have enough data to make meaningful probability and loss estimates.
At the other extreme, if you have virtually no historical risk data, then the categorical technique, with two or three categories of risk probability and associated risk loss, is a reasonable approach. In situations where you are able to categorize risk event likelihood and associated risk impact (which can be monetary or non-monetary loss such as morale effect) into roughly five categories, then the PERIL technique is often a great choice.
Regardless of which of the risk analysis techniques you decide to use in your environment, you must take care to interpret your results cautiously. Keep in mind that risk analysis almost always has very large amounts of variability in the input estimates. In other words, risk analysis gives you guidelines, not rules, to prioritize your software testing efforts.
Risk Resources
For more on risk, see these MSDN Magazine columns:
| "Test Run: Competitive Analysis Using MAGIQ" |
| "Test Run: The Analytic Hierarchy Process" |
Wrapping Up
One part of the overall risk analysis process that I did not discuss in this column is risk management. Risk management entails activities such as establishing a system for entering and storing risk data plus monitoring risk information over time as your software project progresses. Risk management systems can range from an informal system based on e-mail, through a lightweight approach based on Excel spreadsheets, up to a sophisticated approach based on using Risk Items in a Microsoft Team Foundation Server system.
It is important to understand that risk analysis should be an ongoing, iterative process, regardless of how you decide to manage your risk effort. Because software project development is such a dynamic activity, you must revise your risk data and results as the project evolves.
Common sense suggests that software risk analysis should be a part of all software projects. Projects ranging from tiny, one-developer, one-week efforts up to huge, multi-year projects with hundreds or even thousands of developers should have some form of risk analysis. However, there is quite a bit of survey research which shows that risk analyses are often not performed, especially on medium and small software projects.
There are several likely explanations. I suspect that one reason risk analyses are rarely performed is that they require techniques and aptitudes which are nearly opposite of the skills and aptitudes required for coding. Let me explain. Most software development activities are relatively well-defined, based on a closed-system, are micro-goal oriented, and usually provide immediate feedback. For example, when you write some code as a developer, you can get instant feedback when you compile and then execute your code. If your code runs as expected, you typically get a certain amount of satisfaction. Performing software risk analysis is a much different kind of activity. You don't get any of the types of feedback or satisfaction you're used to getting.
My point is that software risk analysis is very different from coding. Hopefully this column has convinced you of the importance of performing risk analysis and shown you some neat techniques to create better, more reliable software.
Send your questions and comments for James to testrun@microsoft.com.
Dr. James McCaffrey works for Volt Information Sciences, Inc., where he manages technical training for software engineers working at Microsoft in Redmond, Washington. He has worked on several Microsoft products, including Internet Explorer and MSN Search, and is the author of .NET Test Automation: A Problem-Solution Approach (Apress, 2006). James can be reached at jmccaffrey@volt.com or v-jammc@microsoft.com.