Note
Access to this page requires authorization. You can try signing in or changing directories.
Access to this page requires authorization. You can try changing directories.
This article describes the methods that AutoML in Azure Machine Learning uses to prepare time series data and build forecasting models.
What you'll learn:
- How AutoML uses time series models and regression models for forecasting
- How AutoML prepares and engineers features from your data
- Which forecasting models are available and when to use them
For instructions and examples about training forecasting models in AutoML, see Set up AutoML for time series forecasting.
Forecasting methods in AutoML
AutoML uses several methods to forecast time series values. You can assign these methods to two categories:
- Time series models that use historical values of the target quantity to make predictions into the future
- Regression, or explanatory, models that use predictor variables to forecast values of the target
Next steps: After understanding these methods, learn how to configure your forecasting job or explore how AutoML selects the best model.
Suppose you need to forecast daily demand for a particular brand of orange juice from a grocery store. For the expression, let $y_t$ represent the demand for this brand on day $t$. A time series model predicts demand at $t+1$ by using some function of historical demand with the following expression:
$y_{t+1} = f(y_t, y_{t-1}, \ldots, y_{t-s})$
The function $f$ often has parameters that you tune by using observed demand from the past. The amount of history that $f$ uses to make predictions, $s$, can also be considered a parameter of the model.
The time series model in the orange juice demand example might not be accurate enough because it uses only information about past demand. Many other factors can influence future demand, such as price, day of the week, and holiday periods. Consider a regression model that uses these predictor variables with the following expression:
$y = g(\text{price}, \text{day of week}, \text{holiday})$
Again, the function $g$ generally has a set of parameters, including values that govern regularization, which AutoML tunes by using past values of the demand and the predictors. You omit $t$ from the expression to emphasize that the regression model uses correlational patterns between contemporaneously defined variables to make predictions. To predict $y_{t+1}$ from $g$, you need to know which day of the week corresponds to $t+1$, whether the day is a holiday, and the orange juice price on day $t+1$. The first two pieces of information are easy to identify by using a calendar. A retail price is commonly set in advance, so the price of orange juice is likely also known one day in advance. However, the price might not be known 10 days into the future. It's important to understand that the utility of this regression is limited by how far into the future you need forecasts, also called the forecast horizon, and to what degree you know the future values of the predictors.
Important
AutoML's forecasting regression models assume that all features you provide are known into the future, at least up to the forecast horizon.
You can also augment AutoML's forecasting regression models to use historical values of the target and predictors. The result is a hybrid model with characteristics of a time series model and a pure regression model. Historical quantities are extra predictor variables in the regression referred to as lagged quantities. The order of the lag refers to how far back the value is known. For example, the current value of an order-two lag of the target for the orange juice demand example is the observed juice demand from two days ago.
Another notable difference between the time series models and the regression models is how they generate forecasts. Recursion relations generally define time series models that produce forecasts one at a time. To forecast many periods into the future, they iterate up to the forecast horizon, feeding previous forecasts back into the model to generate the next one-period-ahead forecast as needed. In contrast, the regression models are considered direct forecasters that generate all forecasts up to the horizon in a single attempt. Direct forecasters can be preferable to recursive methods because recursive models compound prediction error when they feed previous forecasts back into the model. When lag features are included, AutoML makes some important modifications to the training data so the regression models can function as direct forecasters. For more information, see Lag features for time-series forecasting in AutoML.
Forecasting models in AutoML
AutoML in Azure Machine Learning implements the following forecasting models. For each category, the models are listed roughly in order of the complexity of patterns they can incorporate, also known as the model capacity. A Naive model, which simply forecasts the last observed value, has low capacity while the Temporal Convolutional Network (TCNForecaster), a deep neural network (DNN) with potentially millions of tunable parameters, has high capacity.
Learn more about deep learning models: If you're working with complex time series patterns, see Deep learning models (DNN) for forecasting in AutoML.
| Time series models | Regression models |
|---|---|
| Naive, Seasonal Naive, Average, Seasonal Average, ARIMA(X), Exponential Smoothing | Linear SGD, LARS LASSO, Elastic Net, Prophet, K Nearest Neighbors, Decision Tree, Random Forest, Extremely Randomized Trees, Gradient Boosted Trees, LightGBM, XGBoost, TCNForecaster |
AutoML also includes ensemble models that create weighted combinations of the best performing models to further improve accuracy. For forecasting, use a soft voting ensemble where composition and weights are found by using the Caruana Ensemble Selection Algorithm.
Note
There are two important caveats for forecast model ensembles:
- The TCN can't currently be included in ensembles.
- By default, AutoML disables the stack ensemble method, which is included with default regression and classification tasks in AutoML. The stack ensemble fits a meta-model on the best model forecasts to find ensemble weights. During internal benchmarking, this strategy has an increased tendency to overfit time series data. This result can lead to poor generalization, so the stack ensemble is disabled by default. You can enable the ensemble in the AutoML configuration, as needed.
How AutoML uses your data
AutoML accepts time series data in tabular "wide" format. Each variable must have its own corresponding column. AutoML requires one column to be the time axis for the forecasting problem. This column must be parsable into a datetime type. The simplest time series dataset consists of a time column and a numeric target column. The target is the variable you intend to predict into the future. The following table shows example values for this format:
| timestamp | quantity |
|---|---|
| 2012-01-01 | 100 |
| 2012-01-02 | 97 |
| 2012-01-03 | 106 |
| ... | ... |
| 2013-12-31 | 347 |
In more complex cases, the dataset might contain other columns aligned with the time index:
| timestamp | SKU | price | advertised | quantity |
|---|---|---|---|---|
| 2012-01-01 | JUICE1 | 3.5 | 0 | 100 |
| 2012-01-01 | BREAD3 | 5.76 | 0 | 47 |
| 2012-01-02 | JUICE1 | 3.5 | 0 | 97 |
| 2012-01-02 | BREAD3 | 5.5 | 1 | 68 |
| ... | ... | ... | ... | ... |
| 2013-12-31 | JUICE1 | 3.75 | 0 | 347 |
The second example includes a SKU, a retail price, and a flag to indicate whether an item was advertised in addition to the timestamp and target quantity. The second dataset reveals two series: one for the JUICE1 SKU and one for the BREAD3 SKU. The SKU column is a time series ID column because grouping by these column values produces two groups that each contain a single series. Before the model sweep, AutoML does basic validation of the input configuration and data and adds engineered features.
Data length requirements
To train a forecasting model, you need a sufficient amount of historical data. The required amount varies with the training configuration. If you provide validation data, the minimum number of training observations required per time series is expressed as follows:
$T_{\text{user validation}} = H + \text{max}(l_{\text{max}}, s_{\text{window}}) + 1$
In this expression, $H$ is the forecast horizon, $l_{\text{max}}$ is the maximum lag order, and $s_{\text{window}}$ is the window size for rolling aggregation features. If you use cross-validation, the minimum number of observations is expressed as follows:
$T_{\text{CV}} = 2H + (n_{\text{CV}} - 1) n_{\text{step}} + \text{max}(l_{\text{max}}, s_{\text{window}}) + 1$
In this version, $n_{\text{CV}}$ is the number of cross-validation folds and $n_{\text{step}}$ is the CV step size, or offset between CV folds. The basic logic behind these formulas is that you should always have at least a horizon of training observations for each time series, including some padding for lags and cross-validation splits. For more information about cross-validation for forecasting, see Model selection in AutoML.
Missing data handling
The time series models in AutoML require regularly spaced observations in time, which includes cases like monthly or yearly observations where the number of days between observations can vary. Before the modeling process starts, AutoML ensures there are no missing series values and that the observations are regular.
AutoML handles two types of missing data:
- Missing cell values: A value is missing for some cell in the tabular data
- Missing rows: A row is missing that corresponds with an expected observation given the time series frequency
AutoML automatically detects and imputes both types of missing data.
In the first case, AutoML imputes missing values by using common configurable techniques. The following table shows an example of an expected row that's missing:
| timestamp | quantity |
|---|---|
| 2012-01-01 | 100 |
| 2012-01-03 | 106 |
| 2012-01-04 | 103 |
| ... | ... |
| 2013-12-31 | 347 |
This series ostensibly has a daily frequency, but there's no observation for January 2, 2012 (2012-01-02). In this case, AutoML attempts to fill in the data by adding a new row for the missing value. The new value for the quantity column, and any other columns in the data, are then imputed like other missing values. To execute this process, AutoML must recognize the series frequency to be able to fill in observation gaps as demonstrated in this case. AutoML automatically detects this frequency, or, optionally, you can provide it in the configuration.
You can configure the imputation method for supplying missing values in the input. The following table lists the default methods:
| Column type | Default imputation method |
|---|---|
| Target | Forward fill (last observation carried forward) |
| Numeric feature | Median value |
AutoML handles missing values for categorical features during numerical encoding by including another category that corresponds to a missing value. Imputation is implicit in this case.
Automated feature engineering
AutoML generally adds new columns to your data to increase modeling accuracy. Engineered features can include default or optional items.
Default engineered features:
- Calendar features derived from the time index, such as day of the week
- Categorical features derived from time series IDs
- Encoding categorical types to numeric type
Optional engineered features:
- Indicator features for holidays associated with a given region
- Lags of target quantity
- Lags of feature columns
- Rolling window aggregations, like rolling average, of target quantity
- Seasonal decomposition ((Seasonal and Trend decomposition by using Loess (STL))
You can configure featurization from the AutoML SDK by using the ForecastingJob class or from the Azure Machine Learning studio web interface.
Nonstationary time series detection and handling
A time series where the mean and variance change over time is called nonstationary. Time series that exhibit stochastic trends are nonstationary by nature.
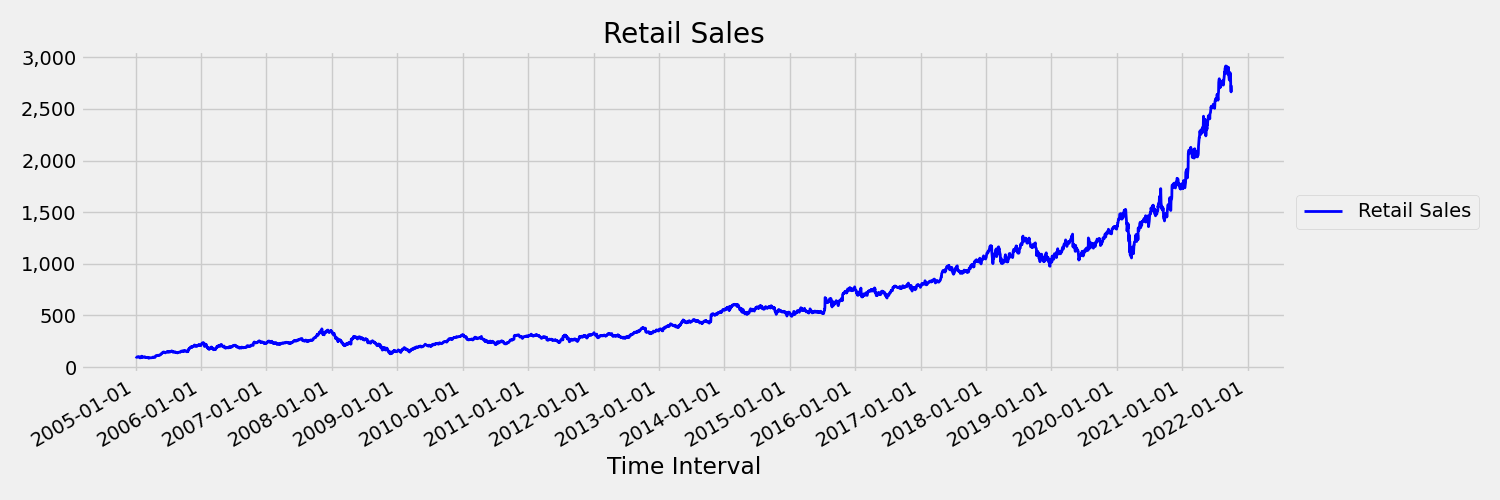
The following image presents a visualization for this scenario. The chart plots a series that's generally trending upward. If you compute and compare the mean (average) values for the first and second half of the series, you can identify the differences. The mean of the series in the first half of the plot is smaller than the mean in the second half. The fact that the mean of the series depends on the time interval under review is an example of the time-varying moments. In this scenario, the mean of a series is the first moment.
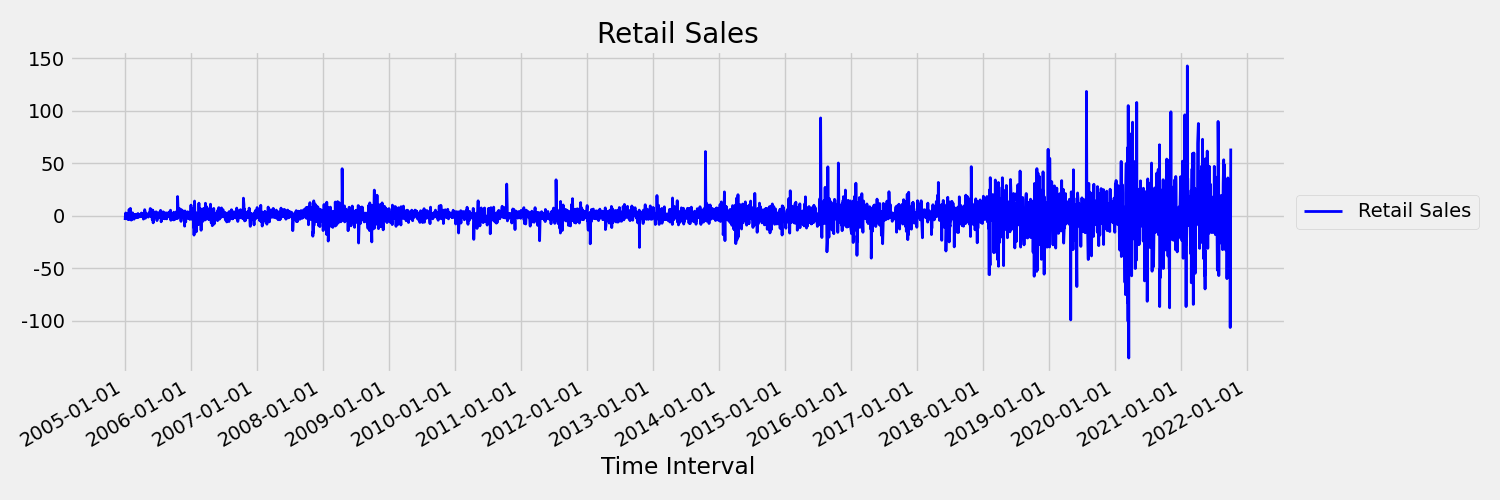
The next image shows a chart that plots the original series in first differences, $\Delta y_{t} = y_t - y_{t-1}$. The mean of the series is roughly constant over the time range while the variance appears to vary. This scenario demonstrates an example of a first-order stationary times series:
AutoML regression models can't inherently deal with stochastic trends or other well-known problems associated with nonstationary time series. As a result, out-of-sample forecast accuracy can be poor when such trends are present.
AutoML automatically analyzes a time series dataset to determine its level or stationarity. When it detects nonstationary time series, AutoML automatically applies a differencing transform to mitigate the effects of nonstationary behavior.
Model sweeping
After data preparation with missing data handling and feature engineering, AutoML sweeps over a set of models and hyperparameters by using a model recommendation service.
The models are ranked based on validation or cross-validation metrics. You can optionally use the top models in an ensemble model. You can inspect, download, or deploy the best model or any of the trained models to produce forecasts as needed. For more information, see Model sweeping and selection for forecasting in AutoML.
Model grouping
When a dataset contains more than one time series, you can model the data in different ways. You can group the data by the time series ID columns and train independent models for each series. A more general approach is to partition the data into groups that each contain multiple (likely related) series and train a model for each group.
By default, AutoML forecasting uses a mixed approach to model grouping. Time series models, plus ARIMAX and Prophet, assign one series to one group. Other regression models assign all series to a single group.
Here's how each model type uses groups:
Each series in a separate group (1:1): Naive, Seasonal Naive, Average, Seasonal Average, Exponential Smoothing, ARIMA, ARIMAX, Prophet
All series in the same group (N:1): Linear SGD, LARS LASSO, Elastic Net, K Nearest Neighbors, Decision Tree, Random Forest, Extremely Randomized Trees, Gradient Boosted Trees, LightGBM, XGBoost, TCNForecaster
You can use the many models solution in AutoML for more general model groupings. For more information, see Many Models - Automated ML notebook.