Compartir a través de

Tutorial: Implementación de un generador cuántico de números aleatorios en Q#

  • Artículo

En este tutorial, aprenderá a escribir un programa cuántico básico en que Q# aproveche la naturaleza de la mecánica cuántica para generar un número aleatorio.

En este tutorial, aprenderá lo siguiente:

  • Cree un Q# programa.
  • Revise los componentes principales de un Q# programa.
  • Definir la lógica de un problema.
  • Combinar operaciones clásicas y cuánticas para resolver un problema.
  • Trabajar con bits cuánticos y con la superposición para crear un generador de números aleatorios cuántico

Sugerencia

Si desea acelerar el recorrido de la computación cuántica, consulte Código con Azure Quantum, una característica única del sitio web de Azure Quantum. Aquí puede ejecutar ejemplos integrados Q# o sus propios Q# programas, generar código nuevo Q# a partir de las indicaciones, abrir y ejecutar el código en VS Code para la Web con un solo clic y hacer preguntas a Copilot sobre la computación cuántica.

Requisitos previos

Definir el problema

Los equipos clásicos no generan números aleatorios, sino números seudoaleatorios. Un generador de números seudoaleatorios genera una secuencia determinista de números a partir de un valor inicial cualquiera, que es el valor de inicialización. Para aproximarse de mejor forma a los valores aleatorios, este valor de inicialización suele ser la hora actual del reloj de la CPU.

Por otro lado, los equipos cuánticos pueden generar números verdaderamente aleatorios. Esto se debe a que la medición de un cúbit en superposición es un proceso probabilístico. El resultado de la medida es aleatorio y no hay ninguna manera de predecir el resultado. Este es el principio básico de los generadores de números aleatorios cuánticos.

Un cúbit es una unidad de información cuántica que puede estar en superposición. Cuando se mide, un cúbit solo puede estar en el estado 0 o en el estado 1. Sin embargo, antes de la medida, el estado del cúbit representa la probabilidad de leer un 0 o un 1 al tomar una medida.

Para comenzar, tome un cúbit en estado base, por ejemplo, cero. El primer paso del generador de números aleatorios es usar una operación Hadamard para colocar el cúbit en una superposición igual. La medición de este estado da como resultado un cero o uno con una probabilidad del 50 % de cada resultado, un bit realmente aleatorio.

No hay forma de saber qué obtendrá después de la medición del cúbit en superposición y el resultado es un valor diferente cada vez que se invoca el código. ¿Pero cómo puede usar este comportamiento para generar números aleatorios mayores?

Supongamos que repetimos el proceso cuatro veces, generando así esta secuencia de dígitos binarios:

$${0, 1, 1, 0}$$

Si concatenamos, o combinamos, estos bits en una cadena de bits, podremos formar un número más grande. En este ejemplo, la secuencia de bits ${0110}$ equivale a seis decimal.

$${0110_{\ binario} \equiv 6_{\ decimal}}$$

Si repite este proceso muchas veces, puede combinar varios bits para formar un número grande. Con este método, puede crear un número para usarlo como contraseña segura, ya que puede estar seguro de que ningún hacker podría determinar los resultados de la secuencia de medidas.

Definición de la lógica del generador de números aleatorios

Vamos a describir cuál debe ser la lógica de un generador de números aleatorios:

  1. Definir max como el número máximo que quiere generar.
  2. Definir el número de bits aleatorios que necesita generar. Para ello, se calcula el número de bits, nBits, debe expresar enteros hasta max.
  3. Generar una cadena de bits aleatorios que tenga una longitud de nBits.
  4. Si la cadena de bits representa un número mayor que max, hay que volver al paso tres.
  5. Si no, el proceso habrá finalizado. Devolver el número generado como un entero.

Como ejemplo, vamos a establecer max en 12. Es decir, 12 es el número más grande que desea usar como contraseña.

Necesita ${\lfloor ln(12) / ln(2) + 1 \rfloor}$ o 4 bits que representen un número entre cero y 12. Podemos usar la función BitSizeIintegrada , que toma cualquier entero y devuelve el número de bits necesarios para representarlo.

Supongamos que generamos la cadena de bits ${1101_{\ binario}}$, que equivale a ${13_{\ decimal}}$. Como 13 es mayor que 12, repetimos el proceso.

Ahora, generamos la cadena de bits ${0110_{\ binario}}$, que equivale a ${6_{\ decimal}}$. Dado que 6 es menor que 12, el proceso se ha completado.

El generador de números aleatorios cuánticos devolverá el número 6 como contraseña. En la práctica, establezca un número más grande como máximo, ya que los números inferiores son fáciles de descifrar simplemente probando todas las contraseñas posibles. De hecho, para aumentar la dificultad de adivinar o descifrar la contraseña, puede usar código ASCII para convertir binario en texto y generar una contraseña mediante números, símbolos y letras en mayúsculas y minúsculas mezcladas.

Escritura de un generador de bits aleatorio

El primer paso es escribir una Q# operación que genera un bit aleatorio. Esta operación será uno de los bloques de creación del generador de números aleatorios.

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Ahora, eche un vistazo al nuevo código.

  • Defina la operación GenerateRandomBit, que no toma ninguna entrada y genera un valor de tipo Result. El tipo Result representa el resultado de una medición y puede tener dos valores posibles: Zero o One.
  • Asigne un solo cúbit con la use palabra clave . Cuando se asigna, un cúbit siempre está en el estado |0〉.
  • Use la H operación para colocar el cúbit en una superposición igual.
  • La operación se usa M para medir el cúbit, devolver el valor medido (Zero o One).
  • Use la Reset operación para restablecer el cúbit al estado |0〉.

Al colocar el cúbit en superposición con la operación H y medirlo con la operación M, el resultado será un valor diferente cada vez que se invoque el código.

Visualización del Q# código con la esfera bloch

En la esfera Bloch, el polo norte representa el valor clásico 0 y el polo sur representa el valor clásico 1. Cualquier superposición se puede representar mediante un punto en la esfera (representado con una flecha). Cuanto más cerca esté el extremo de la flecha a un polo, mayor será la probabilidad de que el cúbit caiga en el valor clásico asignado a ese polo cuando se mida. Por ejemplo, el estado del cúbit representado por la flecha en la ilustración siguiente tiene más probabilidades de dar el valor 0 si lo medimos.

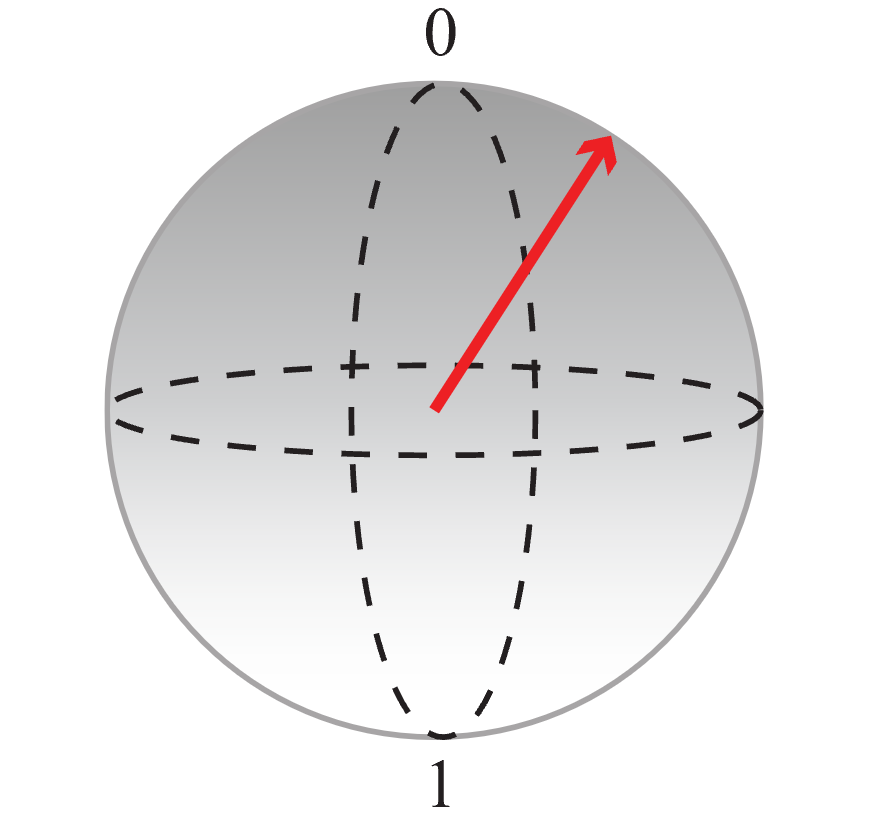
Diagrama que muestra un estado de cúbit con una alta probabilidad de medir cero.

Puede usar esta representación para visualizar lo que está haciendo el código:

  1. En primer lugar, comience con un cúbit inicializado en el estado |0〉 y aplique una H operación para crear una superposición igual en la que las probabilidades de 0 y 1 son las mismas.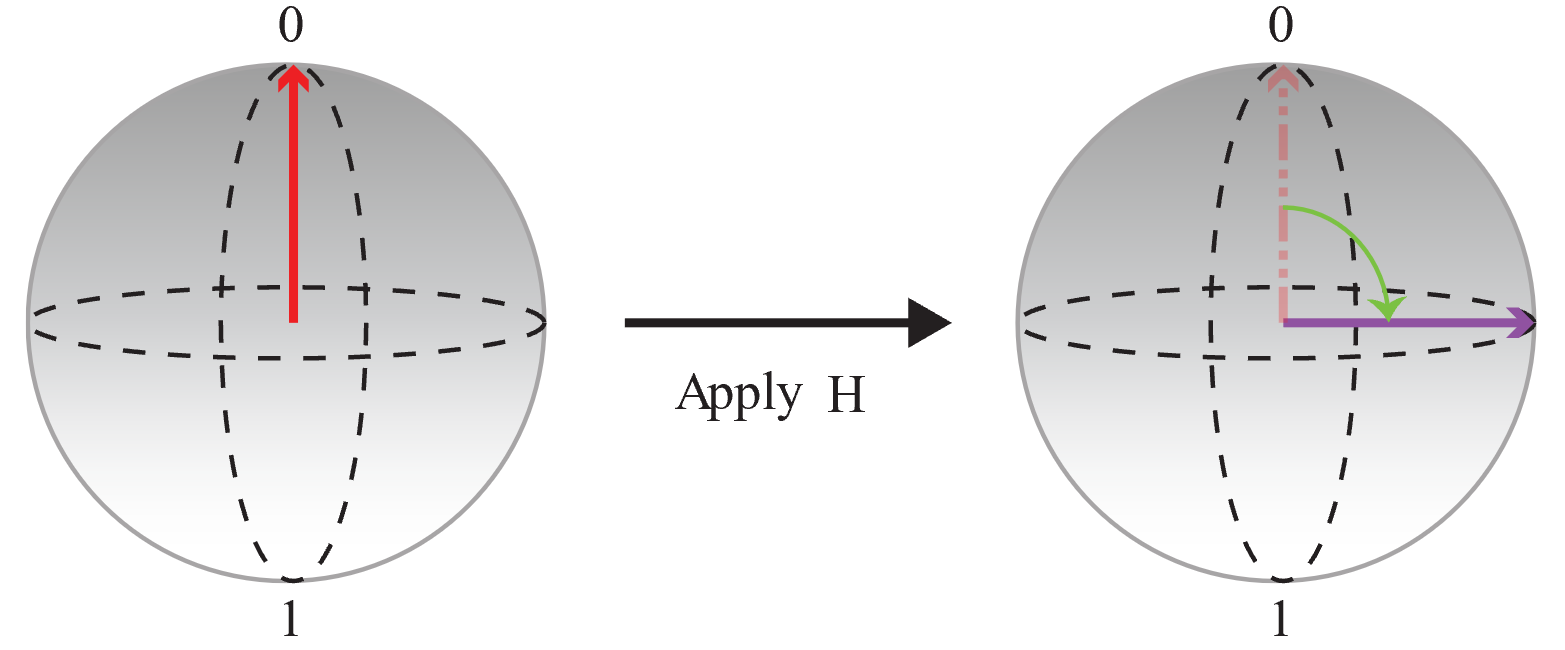

    Diagrama que muestra la preparación de un cúbit en superposición aplicando la puerta hadamard.

  2. A continuación, se mide el cúbit y se guarda el resultado:

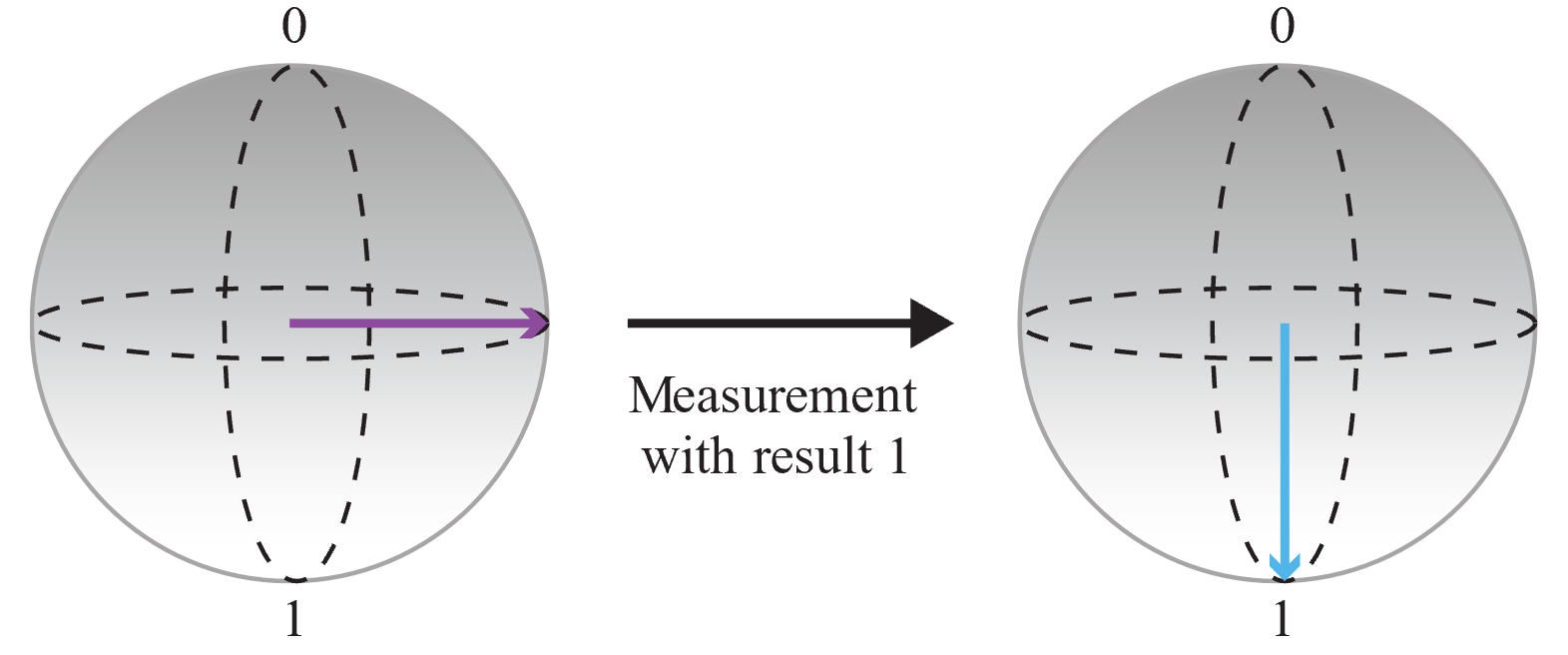
    Diagrama que muestra la medición de un cúbit y el guardado de la salida.

Como el resultado de la medición es aleatorio y las probabilidades de medir 0 y 1 son las mismas, ha obtenido un bit completamente aleatorio. Puede llamar a esta operación varias veces para crear enteros. Por ejemplo, si llama a la operación tres veces para obtener tres bits aleatorios, puede crear números de 3 bits aleatorios (es decir, un número aleatorio entre 0 y 7).

Escribir un generador de números aleatorios completo

  1. En primer lugar, debe importar los espacios de nombres necesarios de la Q# biblioteca estándar al programa. El Q# compilador carga automáticamente muchas funciones y operaciones comunes, pero para el generador de números aleatorios completo, necesita algunas funciones y operaciones adicionales de dos Q# espacios de nombres: Microsoft.Quantum.Mathy Microsoft.Quantum.Convert.

    import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

  2. A continuación, defina la GenerateRandomNumberInRange operación. Esta operación llama repetidamente a la operación GenerateRandomBit para generar una cadena de bits.

    /// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

    Paremos un momento a revisar el nuevo código.

    • Debe calcular el número de bits necesarios para expresar enteros hasta max. La BitSizeI función del Microsoft.Quantum.Math espacio de nombres convierte un entero en el número de bits necesarios para representarlo.
    • La operación SampleRandomNumberInRange usa un bucle for para generar números aleatorios hasta llegar a uno que sea igual o menor que max. El bucle for funciona exactamente igual que un bucle for en otros lenguajes de programación.
    • La variable bits es una variable mutable. Una variable mutable es aquella que puede cambiar durante el cálculo. Para cambiar el valor de una variable mutable, usamos la directiva set.
    • La ResultArrayAsInt función, del espacio de nombres predeterminado Microsoft.Quantum.Convert , convierte la cadena de bits en un entero positivo.

  3. Por último, agregue un punto de entrada al programa. De forma predeterminada, el Q# compilador busca una Main operación e inicia el procesamiento allí. Llama a la GenerateRandomNumberInRange operación para generar un número aleatorio entre 0 y 100.

    operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

    La directiva let declara variables que no cambian durante el cálculo. Aquí se define el valor máximo como 100.

    Para obtener más información sobre la Main operación, vea Puntos de entrada.

  4. El código completo del generador de números aleatorios es el siguiente:

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

Ejecución del programa generador de números aleatorios

Puede ejecutar el programa en Copilot en Azure Quantum y en Visual Studio Code como una aplicación independiente Q# o mediante un programa host de Python.

Puede probar el Q# código con Copilot en Azure Quantum de forma gratuita: todo lo que necesita es una cuenta de correo electrónico de Microsoft (MSA). Para más información sobre Copilot en Azure Quantum, consulte Exploración de Azure Quantum.

  1. Abra Copilot en Azure Quantum en el explorador.

  2. Copie y pegue el código siguiente en el editor de código.

    import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

  3. Seleccione el número de capturas que se van a ejecutar y seleccione Ejecutar.

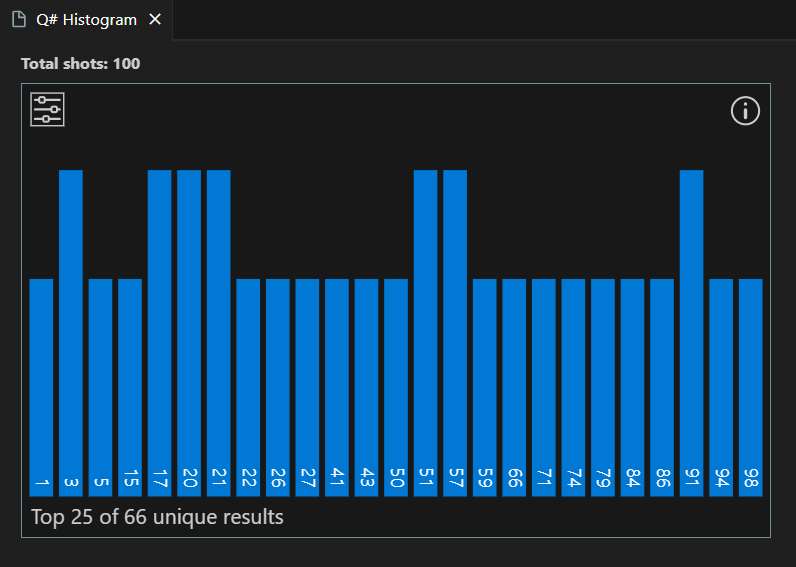
  4. Los resultados se muestran en el histograma y en los campos Resultados .

  5. Seleccione Explicar código para preguntar a Copilot para explicarle el código.

Sugerencia

Desde Copilot en Azure Quantum, puede abrir el programa en VS Code para web seleccionando el botón logotipo de VS Code en la esquina derecha del editor de código.

Nota:

Este fragmento de código no se ejecuta actualmente en ningún hardware targetsde Azure Quantum disponible, ya que el invocable ResultArrayAsInt requiere una QPU con perfil de cálculo completo.

Contenido relacionado

Explore otros tutoriales de Q#:

  • El entrelazamiento cuántico muestra cómo escribir un Q# programa que manipula y mide cúbits y muestra los efectos de la superposición y el entrelazamiento.
  • El algoritmo de búsqueda de Grover muestra cómo escribir un Q# programa que usa el algoritmo de búsqueda de Grover.
  • Las transformaciones de Quantum Fourier exploran cómo escribir un Q# programa que direccione directamente los cúbits específicos.
  • Quantum Katas son tutoriales autodirigido y ejercicios de programación dirigidos a enseñar los elementos de la computación cuántica y Q# la programación al mismo tiempo.