Polilíneas y ecuaciones paramétricas
Uso de SkiaSharp para representar cualquier línea que pueda definirse con ecuaciones paramétricas
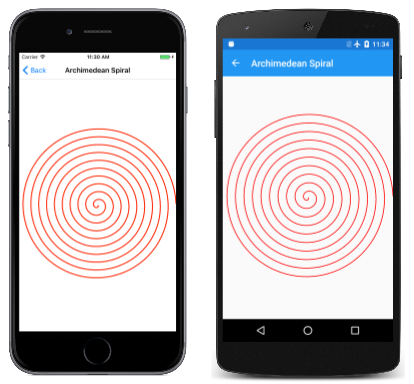
En la sección de Curvas y rutas de SkiaSharp de esta guía, verá los distintos métodos que define SKPath para representar determinados tipos de curvas. Sin embargo, a veces es necesario dibujar un tipo de curva que no es compatible directamente con SKPath. En tal caso, puede usar una polilínea (una colección de líneas conectadas) para dibujar cualquier curva que pueda definir matemáticamente. Si hace que las líneas sean lo suficientemente pequeñas y numerosas, el resultado tendrá un aspecto similar a una curva. Esta espiral es en realidad 3.600 líneas pequeñas:

Por lo general, es mejor definir una curva en términos de un par de ecuaciones paramétricas. Son ecuaciones para coordenadas X e Y que dependen de una tercera variable, a veces denominada t para referirse al tiempo. Por ejemplo, las siguientes ecuaciones paramétricas definen un círculo con un radio de 1 centrado en el punto (0, 0) para t de 0 a 1:
x = cos(2πt)
y = sin(2πt)
Si quiere un radio mayor que 1, simplemente puede multiplicar los valores de seno y coseno por ese radio y, si necesita mover el centro a otra ubicación, agregar esos valores:
x = xCenter + radius·cos(2πt)
y = yCenter + radius·sin(2πt)
Para una elipse con los ejes paralelos a la horizontal y la vertical, hay dos radios implicados:
x = xCenter + xRadius·cos(2πt)
y = yCenter + yRadius·sin(2πt)
A continuación, puede colocar el código SkiaSharp equivalente en un bucle que calcula los distintos puntos y los agrega a una ruta. El siguiente código SkiaSharp crea un objeto SKPath para una elipse que rellena la superficie de visualización. El bucle recorre directamente los 360 grados. El centro es la mitad del ancho y alto de la superficie de visualización, por lo que son los dos radios:
SKPath path = new SKPath();
for (float angle = 0; angle < 360; angle += 1)
{
double radians = Math.PI * angle / 180;
float x = info.Width / 2 + (info.Width / 2) * (float)Math.Cos(radians);
float y = info.Height / 2 + (info.Height / 2) * (float)Math.Sin(radians);
if (angle == 0)
{
path.MoveTo(x, y);
}
else
{
path.LineTo(x, y);
}
}
path.Close();
Esto da como resultado una elipse definida por 360 líneas pequeñas. Cuando se representa, aparece de forma suave.
Por supuesto, no es necesario crear una elipse mediante una polilínea porque SKPath incluye un método AddOval que lo hace automáticamente. Pero es posible que quiera dibujar un objeto visual que SKPath no proporciona.
La página Archimedean Spiral tiene código similar al código de elipse, pero con una diferencia crucial. Recorre en bucle los 360 grados del círculo 10 veces, ajustando continuamente el radio:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
SKPoint center = new SKPoint(info.Width / 2, info.Height / 2);
float radius = Math.Min(center.X, center.Y);
using (SKPath path = new SKPath())
{
for (float angle = 0; angle < 3600; angle += 1)
{
float scaledRadius = radius * angle / 3600;
double radians = Math.PI * angle / 180;
float x = center.X + scaledRadius * (float)Math.Cos(radians);
float y = center.Y + scaledRadius * (float)Math.Sin(radians);
SKPoint point = new SKPoint(x, y);
if (angle == 0)
{
path.MoveTo(point);
}
else
{
path.LineTo(point);
}
}
SKPaint paint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Red,
StrokeWidth = 5
};
canvas.DrawPath(path, paint);
}
}
El resultado también se denomina espiral aritmética porque el desplazamiento entre cada bucle es constante:
Observe que SKPath se crea en un bloque using. SKPath consume más memoria que los objetos SKPath de los programas anteriores, lo que sugiere que un bloque using es más adecuado para eliminar los recursos no administrados.