Ejercicio: Exploración de datos, parte 2: Comprobación de la distribución de los datos

  • 6 minutos

Ha quitado la fila que tenía los valores atípicos en las columnas points y possessions. Pero todavía tiene que solucionar los valores dispersos que faltan. Revise ahora esos valores que faltan:

# Recheck the totals for NaN values by row.
player_df.isna().sum()

ID             0
points         0
possessions    0
team_pace      0
GP             6
MPG            5
TS%            0
AST            0
TO             0
USG            0
ORR            0
DRR            0
REBR           0
PER            9
dtype: int64

Son muchos. Es posible que abarquen muchas más filas y no le gustaría descartar tantos datos. ¿Puede realizar suposiciones fundamentadas sobre con qué los debe rellenar?

Como revisión, en la tabla siguiente se describen los datos con los que trabaja en el conjunto de datos. Los datos de otras columnas se pueden comportar de forma bastante diferente. Por tanto, aplique a los datos la experiencia en la materia a medida que decida cómo imputar los valores que faltan.

Nombre de la columna Descripción
ID Identificador único para cada jugador del conjunto de datos
puntos Número total de puntos obtenidos por un jugador en una temporada
possessions Número total de posesiones de un jugador en una temporada
team_pace Promedio de posesiones que un equipo usa por partido
GP Partidos jugados por un jugador en una temporada
MPG Promedio de minutos jugados por un jugador por partido
TS % Porcentaje de tiro real, el porcentaje de tiro del jugador, que tiene en cuenta los tiros libres y los triples
AST Relación de asistencias, el porcentaje de las posesiones de un jugador que acaban en una asistencia
TO Relación de pérdidas de balón, el porcentaje de las posesiones de un jugador que acaban en una pérdida de balón
USG Tasa de uso, es decir, el número de posesiones de un jugador durante 40 minutos
ORR Tasa de rebotes en ataque
DRR Tasa de rebotes en defensa
REBR Tasa de rebotes, es decir, el porcentaje de tiros fallados que un jugador rebota
PER Clasificación de eficiencia del jugador, es decir, la medida de la productividad por minuto de un jugador en la cancha

Una estrategia de imputación común consiste en reemplazar un valor que falta por el valor inmediatamente superior o inferior. Pero los valores que faltan son para el ritmo, los puntos, las posesiones y PER. Además, desconoce el orden de los jugadores en el objeto DataFrame. Por ejemplo, no sabe si los jugadores consecutivos están en el mismo equipo. Por tanto, aquí probablemente no sea una buena estrategia reemplazar los valores que faltan por valores cercanos.

Otra técnica común consiste en reemplazar los valores que faltan de una columna con el valor promedio de esa columna. Esta técnica podría ser adecuada para estas columnas. Pero debe comprobar cómo se distribuyen los datos de cada columna.

Creación de histogramas de los datos del objeto DataFrame

Una forma habitual de visualizar la distribución de los datos es un histograma. Un histograma es un gráfico de barras en el que se muestra cuántas veces aparecen los datos de un conjunto de datos dentro de un intervalo de valores. Los intervalos se denominan rangos. Generará una vista detallada de los datos mediante 30 rangos para crear histogramas.

No hay ninguna función integrada en Python ni en las bibliotecas de uso frecuente para trazar varios histogramas. Por tanto, creará los histogramas mediante un bucle for como ha hecho con los diagramas de caja.

Nota:

Matplotlib es algo más fácil que Seaborn en lo que a los histogramas se refiere. Simplemente puede trazar los histogramas secuencialmente sin indicar de forma explícita la columna y la fila para cada uno.

# Create a list of all column names, except for 'ID'.
cols = list(player_df.iloc[:, 1:])

# Define the size for the plots and add padding around them.
fig = plt.figure(figsize=(18, 11))
fig.tight_layout(pad=5.0)

# Loop over the columns in the DataFrame and create a histogram for each one.
for i in range(len(cols)):
    plt.subplot(3, 5, i+1)
    plt.hist(player_df[cols[i]], bins=30)
    plt.title(cols[i])

Screenshot showing DataFrame histograms.

La mayoría de estos histogramas no parecen distribuidos normalmente (la conocida curva de campana). Pero es difícil estar seguro a simple vista. Podría intentar usar menos rangos, pero es posible que se pierda información importante en un histograma de menor resolución. En su lugar, pruebe otro tipo de visualización.

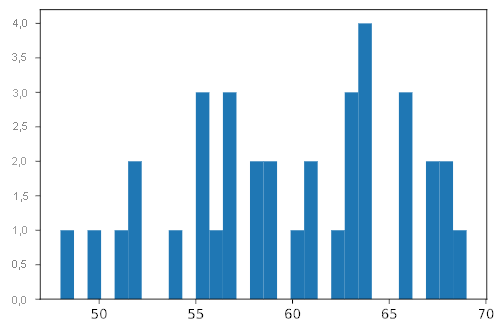
Examine un solo histograma durante un momento. En este caso, analizará el histograma de GP (los partidos jugados).

# Create a histogram for the 'GP' column.
plt.hist(player_df['GP'], bins=30);

Screenshot showing a small-bin histogram.

Nota:

Un punto y coma (;) al final de la llamada a la función hist() hará que la salida muestre solo el gráfico. La salida no mostrará ninguna información textual adicional sobre los datos subyacentes.

Por ejemplo, si quita ; de la línea anterior, verá la salida siguiente antes del gráfico:

(array([1., 0., 1., 0., 1., 2., 0., 0., 1., 0., 3., 1., 3., 0., 2., 2., 0.,
        1., 2., 0., 1., 3., 4., 0., 0., 3., 0., 2., 2., 1.]),
 array([48. , 48.7, 49.4, 50.1, 50.8, 51.5, 52.2, 52.9, 53.6, 54.3, 55. ,
        55.7, 56.4, 57.1, 57.8, 58.5, 59.2, 59.9, 60.6, 61.3, 62. , 62.7,
        63.4, 64.1, 64.8, 65.5, 66.2, 66.9, 67.6, 68.3, 69. ]),
 <a list of 30 Patch objects>)

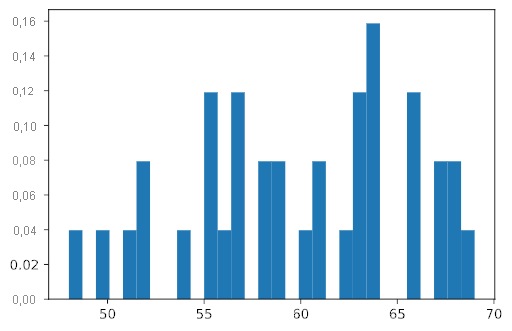
Actualmente, el histograma proporciona el número de recuentos para cada rango. Pero podría cambiar el parámetro density de la función para que el alto de cada columna del histograma muestre la parte que contribuye esa columna al área global del histograma en lugar de recuentos de instancias. Es decir, density=True significa que el área de las columnas del histograma suma hasta 1.

# Create a histogram for the 'GP' column, this time as a probability density.
plt.hist(player_df['GP'], density=True, bins=30);

Screenshot showing a small-bin histogram that includes probability density.

Creación de estimaciones de densidad de kernel de los datos del objeto DataFrame

No tiene que usar rectángulos en el histograma. En su lugar, podría usar triángulos, trapezoides o incluso pequeñas curvas de campana Gaussianas. Esta última forma es básicamente lo que hace la estimación de densidad de kernel (KDE). Crea un histograma de pequeñas curvas de campana. El área bajo las curvas de campana es 1.

Este es el aspecto de la KDE de GP en comparación con un histograma de 15 rangos:

# Plot the KDE for 'GP' over the probability-density histogram.
plt.hist(player_df['GP'], density=True, bins=15)
plt.title('GP histogram')
sns.kdeplot(player_df['GP']);

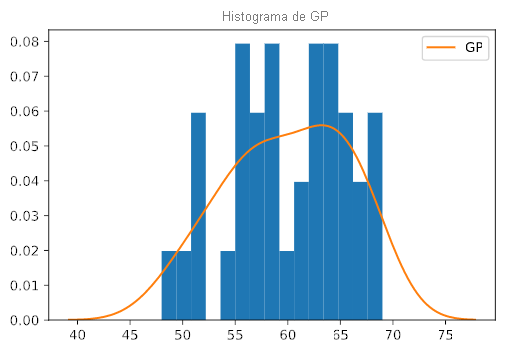
Screenshot showing a large-bin histogram overlaid with K D E.

Con más claridad que el histograma, la KDE ayuda a ver que la distribución de GP tiene forma de campana, con una protuberancia en el lado derecho.

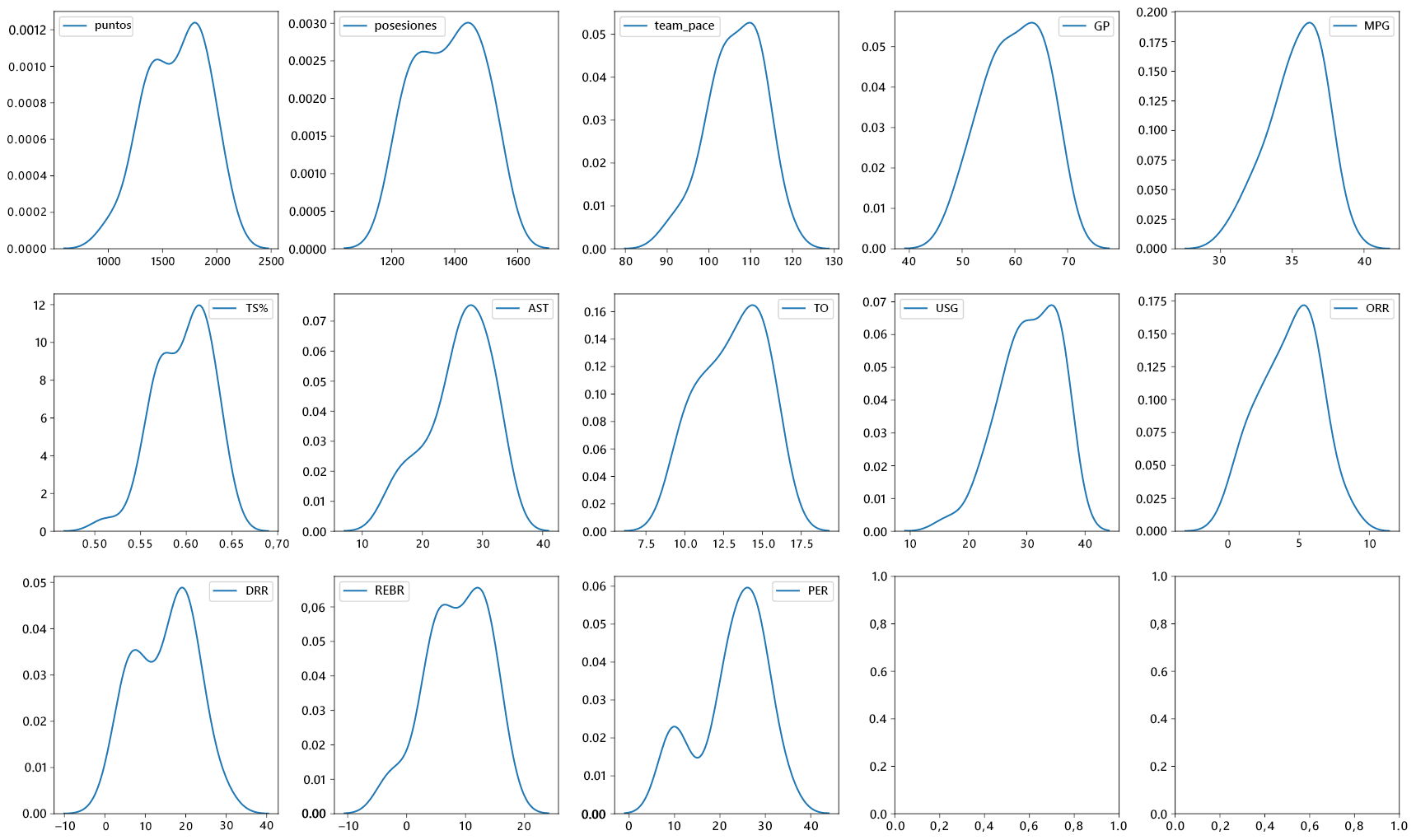
Use un bucle for para generar una matriz de KDE para todas las columnas:

# Create a list of all column names, except for 'ID'.
cols = list(player_df.iloc[:, 1:])

# Create a 3x5 matrix of subplots and add padding around them for readability.
fig, axes = plt.subplots(3, 5, figsize=(18, 11))
fig.tight_layout(pad=2.0)

# Loop over the columns of the DataFrame and create a KDE for each one.
for i in range(len(cols)):
    sns.kdeplot(ax=axes[i//5, i%5], data=player_df[cols[i]])

Screenshot showing DataFrame K D Es.

Es evidente que muchas de estas columnas tienen KDE con dos partes superiores pronunciadas. Cada parte superior representa un modo de los datos, o bien un valor alrededor del que se concentran los valores del conjunto de datos. El hecho de que tantas columnas sean bimodales indica que el conjunto de datos representa ejemplos de dos poblaciones discretas.

© 2021 Warner Bros. Ent. All Rights Reserved.