Función D3DXSHEvalHemisphereLight (D3DX10.h)
Nota
La biblioteca de utilidades D3DX (D3DX 9, D3DX 10 y D3DX 11) está en desuso y no es compatible con las aplicaciones de la Tienda Windows.
Nota
En lugar de usar esta función, se recomienda usar la función de biblioteca matemática armónica esféricaXMSHEvalHemisphereLight.
Evalúa una luz que es una interpolación lineal entre dos colores sobre la esfera.
HRESULT D3DXSHEvalHemisphereLight(
_In_ UINT Order,
_In_ const D3DXVECTOR3 *pDir,
_In_ D3DXCOLOR Top,
_In_ D3DXCOLOR Bottom,
_In_ FLOAT *pROut,
_In_ FLOAT *pGOut,
_In_ FLOAT *pBOut
);
-
Orden [in]
-
Tipo: UINT
Orden de la evaluación armónica esférica (SH). Debe estar en el intervalo de D3DXSH_MINORDER para D3DXSH_MAXORDER, ambos incluidos. La evaluación genera coeficientes Order². El grado de evaluación es Order - 1.
-
pDir [in]
-
Tipo: const D3DXVECTOR3*
Puntero al vector de dirección del eje del hemisferio (x, y, z) en el que se evalúan las funciones de base sh. Vea la sección Comentarios.
-
Top [in]
-
Tipo: D3DXCOLOR
Color del cielo.
-
Inferior [in]
-
Tipo: D3DXCOLOR
Color de suelo.
-
pROut [in]
-
Tipo: FLOAT*
Puntero al vector SH de salida para el componente rojo.
-
pGOut [in]
-
Tipo: FLOAT*
Puntero al vector SH de salida del componente verde.
-
pBOut [in]
-
Tipo: FLOAT*
Puntero al vector SH de salida para el componente azul.
Tipo: HRESULT
Si la función se ejecuta correctamente, el valor devuelto es D3D_OK. Si se produce un error en la función, el valor devuelto puede ser: D3DERR_INVALIDCALL.
La interpolación se realiza linealmente entre los dos puntos, no sobre la superficie de la esfera (es decir, si el eje era (0,0,1) es lineal en Z, no en el ángulo azimutal). La función de iluminación esférica resultante se normaliza para que un punto en una superficie perfectamente difusa sin sombras y un pDir normal apuntado en la dirección pDir daría como resultado una radiación de salida con un valor de 1 (si el color superior era blanco y el color inferior era negro). Se trata de un modelo muy sencillo donde Top representa la intensidad del "cielo" y Bottom representa la intensidad del "suelo".
En la esfera con radio de unidad, como se muestra en la ilustración siguiente, la dirección se puede especificar simplemente con theta, el ángulo sobre el eje z en la dirección derecha y phi, el ángulo de z.
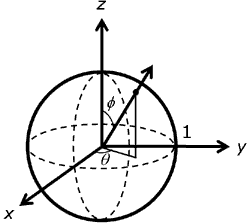
Las ecuaciones siguientes muestran la relación entre las coordenadas cartesianas (x, y, z) y esféricas (theta, phi) en la esfera de unidad. El ángulo theta varía en el intervalo de 0 a 2 pi, mientras que phi varía de 0 a pi.
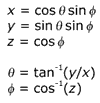
| Requisito | Value |
|---|---|
| Encabezado |
|
| Biblioteca |
|