Compartir a través de

Curvas de parámetros

Los parámetros multimedia pueden seguir una curva a lo largo del tiempo. Cada curva se describe mediante una fórmula matemática y dos puntos finales. Cada punto final se define mediante una hora de referencia y el valor de la curva en ese momento. La fórmula se usa para calcular valores intermedios entre los puntos y determina la forma de la curva. Las posibles curvas son:

  • Saltar
  • Lineal
  • Cuadrado
  • Cuadrado inverso
  • Seno

"Saltar" significa saltar directamente al valor final. Las otras curvas se muestran en el diagrama siguiente.

curvas de parámetro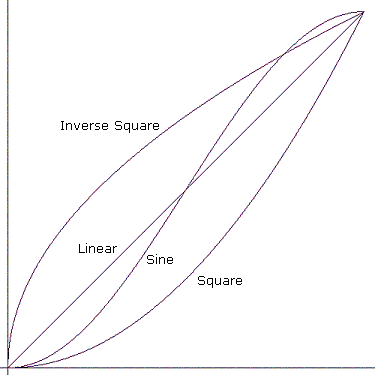

Matemáticamente, las curvas funcionan de la siguiente manera. Supongamos que una curva comienza en el momento t₀ con un valor de v₀ y finaliza a tiempo t₁ con un valor de v₁. Los dos puntos que definen la curva son (t₀, v₀) y (t₁, v₁).

  • Deje que Δt ser la duración total de la curva, t₁–t₀.
  • Deje que Δv ser el intervalo entre los valores inicial y final, v₁–v₀.
  • En cualquier momento t tal que t₀ <= t<= t₁, deje que Δt' = t–t₀.

El valor del parámetro en el momento t es:

v = f( Δt' / Δt ) * Δv + v₀

donde f(x) es una función determinada por el tipo de curva:

  • Lineal: y = x
  • Cuadrado: y = x^2
  • Cuadrado inverso: y = sqrt(x)
  • Sine: y = [ sin(πx – π/2) + 1 ] / 2

Observe que Δt' < Δt, por lo que el término Δt'/Δt oscila entre 0 y 1. Por lo tanto, f(x) también oscila entre 0 y 1 y v siempre cae entre v₀ y v₁. Esto es cierto si v₀ <v₁ o viceversa. Es decir, la curva está limitada por el rectángulo (t₀, v₀, t₁, v₁).

Para la curva seno, el valor de (πx – π/2) oscila entre –π/2 y π/2, lo que significa que sin(πx – π/2) oscila entre –1 y 1. A continuación, el resultado se normaliza para que f(x) entre el intervalo (0-1).

parámetros multimedia