Bezier Splines

Una spline Bézier es una curva especificada por cuatro puntos: dos puntos finales (p1 y p2) y dos puntos de control (c1 y c2). La curva comienza en p1 y termina en p2. La curva no pasa por los puntos de control, pero los puntos de control actúan como imanes, arrastrando la curva en determinadas direcciones e influyen en la forma en que se dobla la curva. En la ilustración siguiente se muestra una curva Bézier junto con sus extremos y puntos de control.

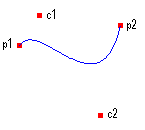
Tenga en cuenta que la curva comienza en p1 y se mueve hacia el punto de control c1. La línea tangente a la curva en p1 es la línea dibujada de p1 a c1. Tenga en cuenta también que la línea tangente en el punto de conexión p2 es la línea dibujada de c2 a p2.

Para dibujar un spline de Bézier, necesita un objetoGraphicsy un objeto Pen. El objeto graphics proporciona el método drawBezier y el objeto pen almacena atributos de la curva, como el ancho de línea y el color. La dirección del objeto Pen se pasa como uno de los argumentos al método DrawBezier. Los argumentos restantes que se pasan al método DrawBezier son los puntos de conexión y los puntos de control. En el ejemplo siguiente se dibuja una spline Bézier con punto inicial (0, 0), puntos de control (40, 20) y (80, 150) y punto final (100, 10).

myGraphics.DrawBezier(&myPen, 0, 0, 40, 20, 80, 150, 100, 10);

En la ilustración siguiente se muestra la curva, los puntos de control y dos líneas tangentes.

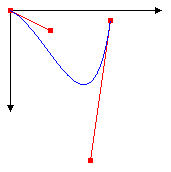
Bézier splines fue desarrollado originalmente por Pierre Bézier para el diseño en la industria automotriz. Desde entonces han demostrado ser muy útiles en muchos tipos de diseño asistido por ordenador y también se usan para definir los contornos de las fuentes. Bézier splines puede producir una amplia variedad de formas, algunas de las cuales se muestran en la ilustración siguiente.

ilustración de