Compartir a través de

Representación de matriz de transformaciones

Una matriz de m×n es un conjunto de números organizados en filas m y columnas n. En la ilustración siguiente se muestran varias matrices.

ilustración de 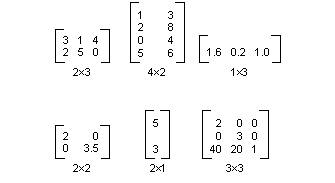que muestra seis matrices de dimensiones variables

Puede agregar dos matrices del mismo tamaño agregando elementos individuales. En la ilustración siguiente se muestran dos ejemplos de adición de matriz.

ilustración de 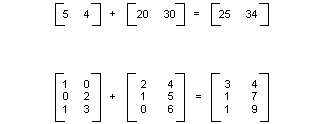que muestra cómo realizar la adición de matriz

Una matriz de m×n se puede multiplicar por una matriz n×p y el resultado es una matriz m×p p. El número de columnas de la primera matriz debe ser el mismo que el número de filas de la segunda matriz. Por ejemplo, una matriz de 4 ×2 se puede multiplicar por una matriz de 2 ×3 para generar una matriz de 4 ×3.

Los puntos del plano y las filas y columnas de una matriz se pueden considerar como vectores. Por ejemplo, (2, 5) es un vector con dos componentes y (3, 7, 1) es un vector con tres componentes. El producto de punto de dos vectores se define de la siguiente manera:

(a, b) • (c, d) = ac + bd

(a, b, c) • (d, e, f) = ad + be + cf

Por ejemplo, el producto de punto de (2, 3) y (5, 4) es (2)(5) + (3)(4) = 22. El producto de punto de (2, 5, 1) y (4, 3, 1) es (2)(4) + (5)(3) + (1)(1) = 24. Tenga en cuenta que el producto de punto de dos vectores es un número, no otro vector. Tenga en cuenta también que solo puede calcular el producto de puntos si los dos vectores tienen el mismo número de componentes.

Deje que A(i, j) sea la entrada de la matriz A en la fila iésima y la columna jésima. Por ejemplo, A(3, 2) es la entrada de la matriz A en la fila 3rd y la columna 2nd. Supongamos que A, B y C son matrices y AB = C. Las entradas de C se calculan de la siguiente manera:

C(i, j) = (fila i de A) • (columna j de B)

En la ilustración siguiente se muestran varios ejemplos de multiplicación de matriz.

ilustración de 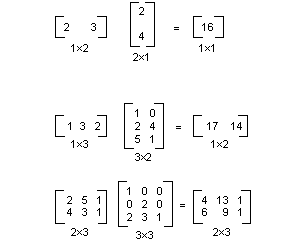que muestra cómo realizar la multiplicación de matrices

Si piensa en un punto del plano como una matriz de 1 × 2, puede transformar ese punto multiplicando por una matriz de 2 × 2. En la ilustración siguiente se muestran varias transformaciones aplicadas al punto (2, 1).

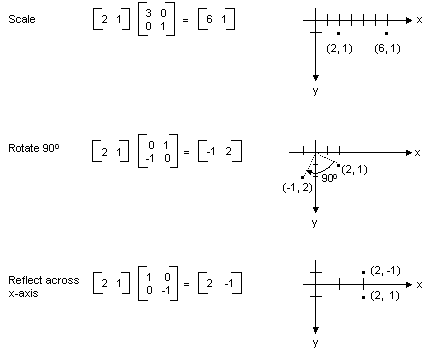
ilustración que muestra cómo usar la multiplicación de matriz para escalar, girar o reflejar un punto en un plano

Todas las transformaciones que se muestran en la ilustración anterior son transformaciones lineales. Algunas otras transformaciones, como la traducción, no son lineales y no se pueden expresar como multiplicaciones por una matriz de 2 × 2. Supongamos que quiere empezar con el punto (2, 1), girarlo 90 grados, traducirlo 3 unidades en la dirección x y traducirlo 4 unidades en la dirección y. Para ello, realice una multiplicación de matriz seguida de una adición de matriz.

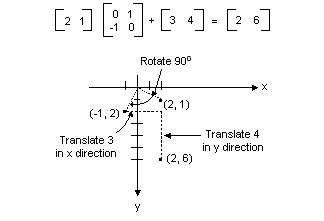
ilustración que muestra cómo la multiplicación y suma de matriz pueden girar un punto y traducirlo dos veces

Una transformación lineal (multiplicación por una matriz de 2 × 2) seguida de una traducción (adición de una matriz de 1 × 2) se denomina transformación affine. Una alternativa a almacenar una transformación afín en un par de matrices (una para la parte lineal y otra para la traducción) es almacenar toda la transformación en una matriz 3 × 3. Para que esto funcione, un punto del plano debe almacenarse en una matriz de 1 × 3 con una coordenada ficticia 3ª. La técnica habitual es hacer que todas las coordenadas 3ª sean iguales a 1. Por ejemplo, el punto (2, 1) se representa mediante la matriz [2 1 1]. En la ilustración siguiente se muestra una transformación afín (girar 90 grados; traducir 3 unidades en la dirección x, 4 unidades en la dirección y) expresadas como multiplicación por una sola matriz de 3 × 3.

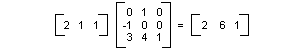
ilustración que muestra cómo la multiplicación de matrices puede realizar una transformación afín

En el ejemplo anterior, el punto (2, 1) se asigna al punto (2, 6). Tenga en cuenta que la tercera columna de la matriz 3 × 3 contiene los números 0, 0, 1. Esto siempre será el caso de la matriz 3 × 3 de una transformación afín. Los números importantes son los seis números de las columnas 1 y 2. La parte superior izquierda 2 × 2 de la matriz representa la parte lineal de la transformación y las dos primeras entradas de la tercera fila representan la traducción.

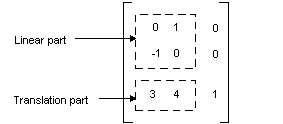
ilustración que muestra que las dos primeras columnas son más significativas para una matriz 3x3 de una transformación afín

En Windows GDI+ puedes almacenar una transformación affine en un objeto matrix. Dado que la tercera columna de una matriz que representa una transformación affine siempre es (0, 0, 1), solo se especifican los seis números de las dos primeras columnas al construir un objeto matrix . La instrucción Matrix myMatrix(0.0f, 1.0f, -1.0f, 0.0f, 3.0f, 4.0f); construye la matriz que se muestra en la ilustración anterior.

Transformaciones compuestas

Una transformación compuesta es una secuencia de transformaciones, una seguida de la otra. Tenga en cuenta las matrices y las transformaciones de la lista siguiente:

  • Matriz A Girar 90 grados
  • Escala de matriz B por un factor de 2 en la dirección x
  • Matriz C Traduce 3 unidades en la dirección y

Si comienza con el punto (2, 1) ( representado por la matriz [2 1 1] y multiplicado por A, B, después C, el punto (2,1) se somete a las tres transformaciones en el orden enumerado.

[2 1 1]ABC = [ –2 5 1]

En lugar de almacenar las tres partes de la transformación compuesta en tres matrices independientes, puede multiplicar A, B y C juntas para obtener una sola matriz de 3 × 3 que almacena toda la transformación compuesta. Supongamos QUE ABC = D. A continuación, un punto multiplicado por D da el mismo resultado que un punto multiplicado por A, después B y C.

[2 1 1]D = [ –2 5 1]

En la ilustración siguiente se muestran las matrices A, B, C y D.

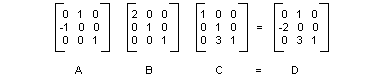
ilustración en la que se muestra cómo realizar varias transformaciones multiplicando las matrices constituyentes

El hecho de que la matriz de una transformación compuesta se pueda formar multiplicando las matrices de transformación individuales significa que cualquier secuencia de transformaciones afín se puede almacenar en un solo objeto matrix Matrix.

Nota

El orden de una transformación compuesta es importante. En general, girar y, a continuación, escalar, traducir no es lo mismo que la escala, luego girar y luego traducir. Del mismo modo, el orden de multiplicación de matriz es importante. En general, ABC no es lo mismo que BAC.

 

La clase Matrix proporciona varios métodos para crear una transformación compuesta: Matrix::Multiply, Matrix::Rotate, Matrix::RotateAt, Matrix::Scale, Matrix::Sheary Matrix::Translate. En el ejemplo siguiente se crea la matriz de una transformación compuesta que gira primero 30 grados, luego se escala por un factor de 2 en la dirección y y y, a continuación, se traducen 5 unidades en la dirección x.

Matrix myMatrix;
myMatrix.Rotate(30.0f);
myMatrix.Scale(1.0f, 2.0f, MatrixOrderAppend);
myMatrix.Translate(5.0f, 0.0f, MatrixOrderAppend);

En la ilustración siguiente se muestra la matriz.

ilustración que muestra una matriz con valores expresados como funciones trigonométricas y una matriz con valores aproximados de esas funciones