Algoritmos de creación de transformación de WCS

2023-06-03

creación de transformaciones optimizadas

conservación negra y de generación negra

Creación de transformaciones

Para explicar correctamente cómo funcionan las transformaciones de color, resulta útil explicar la ruta de procesamiento completa a través de ICM 2.0 y los internos del CTE. La funciónICM 2.0CreateColorTransformW crea una transformación de color que las aplicaciones pueden usar para realizar la administración de colores. Esta función crea un contexto de color a partir de la LOGCOLORSPACE y las entradas de intención. Las intenciones se asignan al algoritmo de asignación de la gama ICC de línea base correlacionada. A continuación, la función llama a la función ICM 2.0 CreateMultiProfileTransform para un procesamiento de color coherente. La función CreateColorTransform copia generalmente los datos en la estructura de transformación optimizada interna.

La función CreateMultiProfileTransform de ICM 2.0 acepta una matriz de perfiles y una matriz de intenciones o un único perfil de vínculo de dispositivo y crea una transformación de color que las aplicaciones pueden usar para realizar la asignación de colores. Procesa esos perfiles y intenciones de entrada para crear modelos de dispositivo, modelos de apariencia de color, descripciones de límites de gama y modelos de asignación de gama. Así es como se hace esto:

Los modelos de dispositivo se inicializan directamente desde perfiles dm. Hay un modelo de dispositivo creado para cada perfil de la llamada a CreateMultiProfileTransform.
Los modelos de apariencia de color se inicializan directamente desde perfiles CAM. Hay un perfil CAM para cada perfil de la llamada a CreateMultiProfileTransform. Sin embargo, se puede especificar el mismo perfil cam para más de un perfil.
Las descripciones de límites de gama se inicializan a partir de un objeto de modelo de dispositivo y un objeto CAM. Hay una descripción de límite de gama para cada perfil de la llamada a CreateMultiProfileTransform.
Los modelos de asignación de gamut se inicializan a partir de dos límites de gama y una intención. Debe crear un modelo de asignación de gama entre cada par de modelos de dispositivo creados a partir de la llamada a CreateMultiProfileTransform. Tenga en cuenta que esto significa que se usa un modelo de asignación de mutación menor que el modelo de dispositivo. Dado que el número de intenciones coincide con el número de modelos de dispositivo, también hay una intención más de la necesaria. Se omite la primera intención de la lista. Puede recorrer la lista de modelos de dispositivo y intenciones, creando modelos de asignación de gama. Elija los modelos de dispositivo primero y segundo y la segunda intención y, a continuación, inicialice el primer modelo de asignación de gama. Elija los modelos de dispositivo segundo y tercero y la tercera intención e inicialice el segundo modelo de asignación de gama. Continúe de esta manera hasta que haya creado todos los modelos de asignación de gama.

Cuando los perfiles se han procesado correctamente y se han creado e inicializado todos los objetos intermedios, puede crear la transformación CITE con la siguiente llamada. El pDestCAM de y pDestD M son los asociados con el último perfil de la llamada a CreateMultiProfileTransform.

HRESULT CreateCITEColorTransform(
 __inout     IDeviceModel          *pSourceDM,
 __inout     IColorAppearanceModel *pSourceCAM,
 __in        GamutMapArray         *pGamutMapArray,
 __inout     IColorAppearanceModel *pDestCAM,
 __inout     IDeviceModel          *pDestDM,
             EColorTransformMode    eTransformMode,
 __deref_out IColorTransform      **ppCTS
 );

Compatibilidad con complementos

Un problema relacionado con la configuración de la lista de transformaciones es validar si hay disponible un complemento necesario. El siguiente modificador de modelo proporciona esta directiva para controlar este comportamiento. La administración de esta lista de transformaciones es un método en la estructura de transformación optimizada interna, pero cada método de modelo proporciona el puntero a sí mismo y su propio conjunto de valores de parámetro.

El modo debe ser uno de los siguientes.

TfmRobust: si un perfil de medida especifica un complemento preferido y el complemento no está disponible, el nuevo sistema CTE usará el complemento de línea base. Si ninguno de los complementos está disponible, la transformación notificará un error.
TfmStrict: si ColorContext especifica un complemento preferido, el complemento debe estar disponible. Si no se encuentra ningún complemento preferido, se usará el complemento de línea base. Si ninguno de los complementos está disponible, la transformación notificará un error.
TfmBaseline: solo se pueden usar complementos de línea base en AddMeasurementStep. Si ColorContext especifica un complemento preferido, se omitirá el complemento. Si el complemento de línea base no está disponible, la transformación notificará un error.

Transformación de la ejecución

La API ICM 2.0 función TranslateColors traduce una matriz de colores del espacio de color de origen al espacio de colores de destino tal como se define en una transformación de color. Esta función comprueba internamente en una matriz de colores almacenados en caché para permitir la coincidencia inmediata de colores comúnmente transformados. Esta transformación admite matrices de bytes de 8 bits por canal y matrices float de 32 bits por canal. Todos los demás formatos se convertirán antes de pasar al nuevo CTE.

La API de ICM 2.0 TranslateBitmapBits función traduce los colores de un mapa de bits que tiene un formato definido para generar otro mapa de bits en un formato solicitado. Esta función comprueba internamente en una matriz de colores almacenados en caché para permitir la coincidencia inmediata de colores comúnmente transformados. Para evitar demasiadas rutas de acceso de código, compatibilidad y complejidad de pruebas, solo se admite un número limitado de formatos de mapa de bits en el motor de transformación e interpolación. Esta función debe traducir los formatos de mapa de bits entrantes y salientes no nativos a formatos admitidos de forma nativa para su procesamiento. Esta transformación solo admite mapas de bits de bytes de 8 bits por canal y mapas de bits flotantes de 32 bits por canal. Todos los demás formatos se convertirán antes de pasar al nuevo CTE.

Ejecución de transformación secuencial

Si el parámetro dwFlags tiene el SEQUENTIAL_TRANSFORM bit establecido cuando se llama a las funciones ICM createColorTransformW o se llama a createMultiProfileTransform, los pasos de transformación se ejecutan secuencialmente. Esto significa que el código recorre cada modelo de dispositivo, modelo de apariencia de color y modelo de asignación de gama por separado, según lo especificado por la llamada CreateColorTransform o CreateMultiProfileTransform. Esto puede resultar útil para depurar módulos de complemento, pero es mucho más lento que ejecutarse a través de una transformación optimizada. Por lo tanto, no se recomienda ejecutar en modo secuencial para el software de producción. Además, puede haber pequeñas diferencias en los resultados obtenidos en modo secuencial y en modo optimizado. Esto se debe a variaciones introducidas cuando las funciones se concatenan juntas.

Creación de transformaciones optimizadas

Una transformación optimizada es una tabla de búsqueda multidimensional. La tabla se puede procesar mediante un motor de interpolación multidimensional, como la interpolación tetrahedral, que aplica los colores de entrada a la transformación. En la sección siguiente se describe cómo se crean las tablas de búsqueda optimizadas. En la sección posterior se describe cómo interpolar dentro de las tablas de búsqueda optimizadas.

Tablas de búsqueda dispersas

Las impresoras convencionales tienen tintas CMYK. Para ampliar la gama, un enfoque es agregar nuevas entradas de lápiz al sistema. Las tintas normalmente agregadas son colores que las tintas CMYK tienen dificultades para reproducirse. Las opciones comunes son naranja, verde, rojo, azul, etc. Para aumentar la "resolución aparente", se pueden usar tintas con diferentes tinciones, por ejemplo, cian ligera, magenta claro, etc. En efecto, el dispositivo de impresora tiene más de cuatro canales.

Aunque las impresoras son dispositivos de salida, también realizan la conversión de color desde el espacio del dispositivo a otro espacio de color. En el caso de una impresora CMYK, esta sería una transformación de CMYK a XYZ, o el "modelo hacia delante" de la impresora. Al combinar el modelo de reenvío con otras transformaciones, es posible emular una impresión cmYK en otro dispositivo. Por ejemplo, una impresora CMYK en un monitor RGB haría posible un mecanismo de corrección que emula una impresión de esa impresora CMYK en un monitor. Del mismo modo, también se aplica para hi-fi impresoras. Una conversión CMYKOG a RGB permite la corrección de la impresora CMYKOG en un monitor.

El enfoque convencional para implementar dicha conversión de color es mediante un LUT uniforme. Por ejemplo, en un perfil ICC para una impresora CMYKOG, la especificación ICC exige una etiqueta A2B1 que almacena un LUT uniforme que representa un muestreo uniforme en el espacio de dispositivo CMYKOG del modelo de reenvío, que va de CMYKOG al espacio de conexión del perfil ICC (ya sea CIELAB o CIEXYZ). El perfil de vínculo de dispositivo ICC permite una transformación directa del espacio del dispositivo CMYKOG a cualquier espacio de color, incluido un espacio de dispositivo, también en forma de LUT muestreado uniformemente en el espacio CMYKOG. El muestreo nunca se realiza con 256 niveles (profundidad de bits 8) debido a la enorme LUT resultante, excepto en el caso de dispositivos monocromáticos (1 canal). En su lugar, se usa el muestreo con profundidad de bits inferior; algunas opciones típicas son 9 (profundidad de bits 3), 17 (profundidad de bits 4), 33 (profundidad de bits 5). Con el número de niveles inferiores a 256 en cada canal, la LUT se usa junto con un algoritmo de interpolación para generar el resultado si un nivel está entre dos niveles muestreados.

Aunque un LUT uniforme es conceptualmente sencillo de implementar y la interpolación en un LUT uniforme es generalmente eficaz, el tamaño de LUT aumenta exponencialmente con la dimensión de entrada. De hecho, si d es el número de pasos utilizados en el LUT uniforme, y n es el número de canales en el espacio de color de origen, el número de nodos de la LUT es 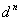Muestra la variable para el número de nodos de un LUT. . Claramente, el número de nodos exige rápidamente tanto almacenamiento en memoria que incluso los sistemas informáticos de primera línea tienen dificultades para controlar la demanda. En el caso de los dispositivos con seis o ocho canales, una implementación icc del perfil de dispositivo requiere el uso de pocos pasos en la LUT, a veces incluso hasta cinco pasos en la tabla A2B1 para mantener el perfil dentro de megabytes en lugar de gigabytes. Claramente, el uso de un número menor de pasos aumenta el error de interpolación, ya que ahora hay menos muestras. Dado que la LUT debe ser uniforme, la precisión en todo el espacio de color se degrada incluso en esas regiones del espacio donde una diferencia de color significativa puede deberse a pequeños cambios en el valor del dispositivo.

En los dispositivos con más de cuatro colorantes, ciertos subespacios de todo el espacio del dispositivo son más importantes que otros. Por ejemplo, en el espacio CMYKOG, las tintas cian y verde rara vez se usan juntas porque sus tonos se superponen en gran medida entre sí. De forma similar, las tintas amarillas y naranjas se superponen en gran medida entre sí. Una reducción uniforme del número de pasos se puede ver como una degradación general de la calidad en todo el espacio de color, que es algo que se puede permitir para las combinaciones de tinta improbables, pero no para las combinaciones probables o importantes.

Aunque un LUT muestreado uniformemente es sencillo y eficaz para la interpolación, impone enormes requisitos de memoria a medida que aumenta la dimensión. En realidad, aunque un dispositivo puede tener seis o ocho canales, rara vez se usan simultáneamente. En la mayoría de los casos, el color de entrada para la transformación de color tiene solo unos pocos colorantes "activos", por lo que reside en un espacio de color dimensional inferior. Esto también significa que la interpolación se puede realizar de forma más eficaz en ese espacio dimensional inferior porque la interpolación es más rápida cuando la dimensión es inferior.

Por lo tanto, el enfoque consiste en estratificar todo el espacio del dispositivo en subespacios de varias dimensiones. Y dado que las dimensiones más bajas (que combinan tres o cuatro colorantes) son más importantes, al autenticar el espacio, también se pueden aplicar diferentes frecuencias de muestreo; es decir, un número diferente de pasos, a las piezas; aumentar las tasas de muestreo para las dimensiones más bajas, lo que las reduce para dimensiones más altas.

Para corregir notaciones, n es el número de canales en el espacio de color de origen de la transformación de color que desea muestrear. También puede hacer referencia a n como dimensión de entrada y 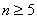Muestra n mayor o igual que 5. , a menos que se especifique lo contrario.

Los bloques de creación básicos son LUT de varias dimensiones de entrada y tamaños, en lugar de un LUT uniforme con dimensión de entrada n. Para ser más precisos, unaLUT es una entramado rectangular impuesta en un cubo unitario; es decir, todas las coordenadas del dispositivo se normalizan en el intervalo [0, 1]). si es la dimensión de entrada del lut (tenga en cuenta que no tiene que ser igual a n, aunque 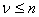Muestra V menor o igual que n. es obligatorio), se compone de cuadrículas de muestreo unidimensionales:

Samp i: 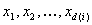Muestra una cuadrícula de muestreo unidimensional.

donde todas las x_j deben estar en el intervalo [0, 1], 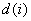Muestra un superíndice d(i). es el número de pasos para el muestreo de canal de i que debe ser al menos 1 y 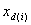Muestra un spuperscript de X (subíndice) d(i). debe ser 1. Por otro lado, 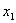Muestra un superíndice X (subíndice 1). no es necesario que sea 0.

Solo se definirán los dos casos especiales siguientes de LUT.

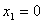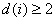LUT cerrada: se trata de un LUT con el requisito adicional de que para cada Samp*_i*, Muestra un superíndice X (subíndice 1) igual a 0. , y Muestra un superíndice d(i) mayor o igual que 2. . Un LUT cerrado uniforme es un LUT cerrado que tiene la misma 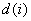Muestra un superíndice d(i). para cada canal y los nodos están espaciados uniformemente entre 0 y 1.

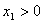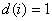open LUT: se trata de un LUT con el requisito adicional de que para cada Samp, SHows a superíndice X (subíndice 1) mayor que 0. . Es correcto tener Muestra un superíndice d(i) igual a 1. .

El objetivo es estratificar el cubo de unidad [0, 1] n en una colección de LUT cerradas y LUT abiertas, de modo que toda la colección cubra el cubo de unidad. Conceptualmente es más sencillo organizar estos "estratos LUT" por sus dimensiones, de modo que en el nivel superior:

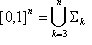
Muestra el nivel superior para organizar los estratos L U T por sus dimensiones.

donde 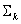muestra el subíndice k. es la colección "k -dimensional strata". Tenga en cuenta que la dimensión strata comienza de 3 en lugar de 0; es decir, puntos, porque la interpolación de combinaciones de tres colores se puede controlar sin demasiado requisito de memoria.

Descripción de los estratos LUT

En esta implementación:

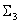consta de LUT cerradas con tres entradas, una de cada combinación posible de tres colorantes elegidas fuera de las n colorantes.
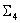consta de un LUT cerrado para la combinación CMYK (o los cuatro primeros colorantes), junto con 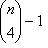LUT abiertas para las demás combinaciones de cuatro colores. Al descartar la combinación CMYK, reconoce que es una combinación importante.
Para 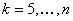, 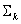consta de 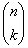LUT abiertas, una para cada posible combinación de elegir k colorantes del total de n colorantes.

Permanece para especificar los tamaños de las LUT. La diferencia clave entre las LUT abiertas y cerradas es que las LUT abiertas no se superponen y las LUT cerradas pueden superponerse en las caras de límite. El hecho de que el muestreo unidimensional en una LUT abierta no contenga 0, básicamente significa que falta una LUT abierta a la mitad de las caras de límite, por lo que el nombre "abierto". Si dos LUT no se superponen, puede usar un número diferente de pasos o ubicaciones de nodo en cada canal. Lo mismo no es cierto si dos LUT se superponen. En ese caso, si el número de pasos o las ubicaciones del nodo son diferentes, un punto que se encuentra en la intersección de los dos LUT recibirá un valor de interpolación diferente dependiendo de qué LUT se use en la interpolación. Una solución sencilla a este problema es usar el muestreo uniforme con el mismo número de pasos cada vez que dos LUT se superponen. En otras palabras:

Todas las LUT cerradas (las LUT de tres colores y la CMYK LUT en esta implementación) deben ser uniformes y tienen el mismo número de pasos, que se indican d.

Los dos algoritmos siguientes se pueden usar para determinar el número de pasos d para LUT cerradas y el número de pasos para luT abiertos.

Algoritmo n.º 1

Este algoritmo no requiere entrada externa.

Todas las LUT cerradas serán uniformes con d número de pasos.

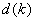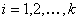Todas las LU abiertas de dimensión k tendrán el mismo número de pasos Muestra d(k). en cada canal de entrada y los nodos están igualmente espaciados; es decir, para cada Muestra i igual a 1, 2, ..., k. .

Samp i: Muestra el algoritmo samp i.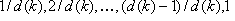

Por último, especifique d y d (k ) en la tabla 1 siguiente. Los tres modos, "prueba", "normal" y "mejor" son la configuración de calidad ICM 2.0. En esta implementación, el modo de prueba tiene la superficie de memoria más pequeña y el mejor modo tiene la superficie de memoria más grande.

Para implementar este algoritmo, debe llamar al siguiente algoritmo #2. Los usuarios pueden especificar sus propias ubicaciones de muestreo mediante las tablas como guía.

Algoritmo n.º 2

Este algoritmo requiere una entrada externa en forma de una lista de ubicaciones de muestreo "importantes", pero es más adaptable y puede ahorrar espacio de memoria potencialmente.

La entrada necesaria es una matriz de valores de dispositivo proporcionados por el usuario. Estos valores de dispositivo indican qué región del espacio de color del dispositivo es importante; es decir, qué región se debe muestrear más.

Todas las LUT cerradas serán uniformes con d número de pasos, tal como se describe en Algoritmo n.º 1. Los valores de d se proporcionan en la tabla 1.

(a) LUT cerrado uniforme

	Modo de prueba	Modo normal	Mejor modo
d	9	17	33

(b) LUT abierto

Dimensión de entrada	Modo de prueba	Modo normal	Mejor modo
4	5	7	9
5	2	3	3
6	2	3	3
7	2	2	2
8 o más	2	2	2

tabla 1: tamaños de LUT usados en el algoritmo

Cada LUT abierta puede tener un número diferente de pasos en cada canal de entrada y las ubicaciones de muestreo no tienen que estar espaciadas iguales. Para un estrato LUT abierto determinado, hay una combinación de colorante asociada, por ejemplo, 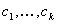muestra el subíndice C 1, ..., subíndice C k. , donde el subíndice 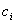Muestra C i. s son enteros distintos entre 1 y n. Son los índices de canal correspondientes a los coloreados "activos" de este estrato.

PASO 1: Filtre la matriz de valores de dispositivo de entrada que no están contenidos en este estrato. Un valor de dispositivo 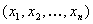Muestra X subíndice 1, X subíndice 2, ..., X subíndice n. se encuentra en el estrato, si y solo si 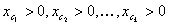Muestra un conjunto de valores para un canal. y todos los demás canales son 0. Si el conjunto filtrado tiene N entradas, deje

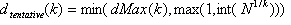
Muestra una ecuación que se va a usar si el conjunto filtrado tiene N entradas.

Para cada 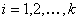Muestra i igual a 1, 2, ..., k. , itera los pasos siguientes 2-5:

PASO 2: Si 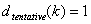muestra d subíndice provisional (k) igual a 1. , Samp i tiene solo 1 punto, que debe ser 1.0. Vaya al siguiente i. De lo contrario, continúe con el PASO 3.

PASO 3: Ordene las muestras filtradas en orden ascendente en el 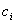muestra el subíndice C i. canal.

PASO 4: Definir la cuadrícula de muestreo "provisional" mediante los nodos

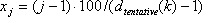
Muestra los nodos usados para definir la cuadrícula de muestreo

donde 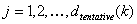Muestra j igual a 1, 2, ..., d subíndice provisional (k). .

PASO 5: Regularice la cuadrícula provisional para asegurarse de que se ajusta a la monotonicidad estricta y también que termina con 1.0. Dado que la matriz ya está ordenada, los nodos de la cuadrícula provisional ya son no descreantes monotónicos. Sin embargo, los nodos adyacentes pueden ser idénticos. Puede corregirlo quitando nodos idénticos, si es necesario. Por último, después de este procedimiento, si el punto final es menor que 1.0, reemplácelo por 1.0.

Tenga en cuenta que el PASO 5 es la razón por la que los estratos LUT pueden tener un número diferente de pasos en cada canal. Después de la regularización, el número de pasos de un canal puede ser menor que 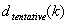Muestra d subíndice provisional (k). .

Interpolación

Puede construir la estratificación del cubo de unidad mediante strata LUT abierta y estratos LUT cerrados. Para realizar la interpolación mediante esta "estructura LUT dispersa", siga estos pasos. Supongamos que un valor de dispositivo de entrada determinado 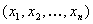Muestra (X subíndice 1, X subíndice 2, ..., X subíndice n). .

PASO 1: Determinar el número de canales "activos". Este es el número de canales distintos de cero. Esto determina la dimensión strata k buscar el estrato contenedor. Más precisamente, la dimensión strata es 3 si el número de canales activos es 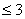Muestra menos o igual que 3. , de lo contrario, la dimensión strata es igual que el número de canales activos.

PASO 2: En 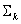muestra el subíndice sigma k. , busque el estrato contenedor. Un valor de dispositivo se encuentra en un estrato abierto si todos los canales correspondientes al estrato tienen un valor distinto de cero y todos los demás canales son cero. Un valor de dispositivo se encuentra en un estrato cerrado si cada canal no representado por el estrato es cero. Si no se encuentra ningún estrato contenedor, hay una condición de error. Cancelación y notificación de errores. Si se encuentra un estrato contenedor, continúe con el paso siguiente.

PASO 3: Si el estrato contenedor está cerrado, cualquier algoritmo de interpolación conocido puede realizar la interpolación dentro del estrato. En esta implementación, la elección del algoritmo es la interpolación tetrahedral. Si el estrato contenedor está abierto y el valor del dispositivo se encuentra estrictamente dentro del estrato, es decir,

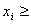Muestra X subíndice i mayor o igual que... primer nodo de i canal

donde i es un índice de canal para el estrato y, a continuación, funciona el algoritmo de interpolación estándar, como la interpolación tetrahedral.

Si 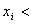muestra X subíndice i menor que... primer nodo de i canal para algunos i, el valor del dispositivo entra en la "brecha" entre el estrato y los subespacios dimensionales inferiores. Este MOI no se preocupa por un algoritmo de interpolación por se, por lo que cualquier algoritmo de interpolación se puede usar para interpolar dentro de esta "brecha", aunque el algoritmo preferido es la siguiente interpolación transfinida.

La arquitectura del módulo de interpolación se muestra en las dos partes de la figura 1.

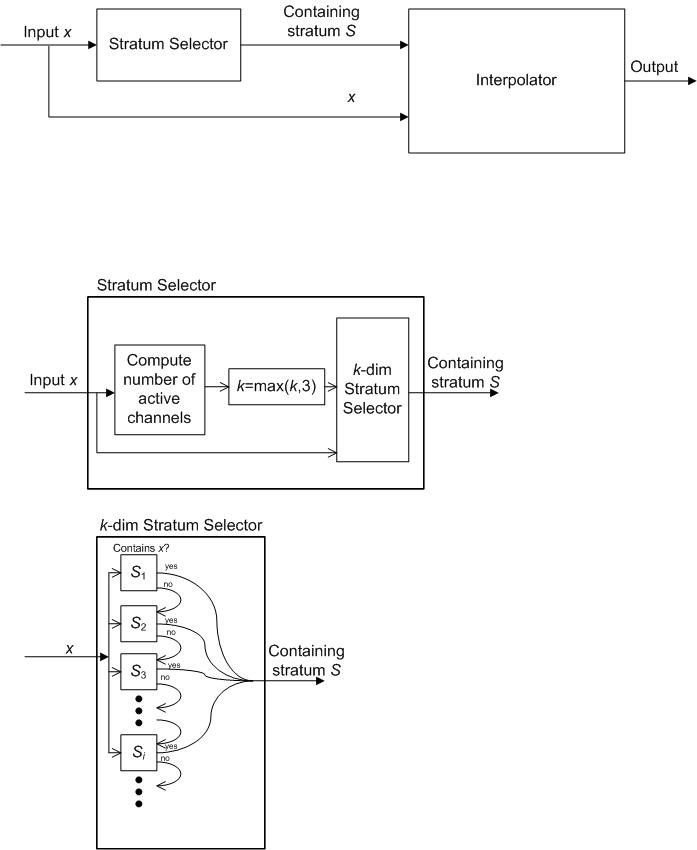
Diagrama que muestra la parte uno de la arquitectura del módulo de interpolación.

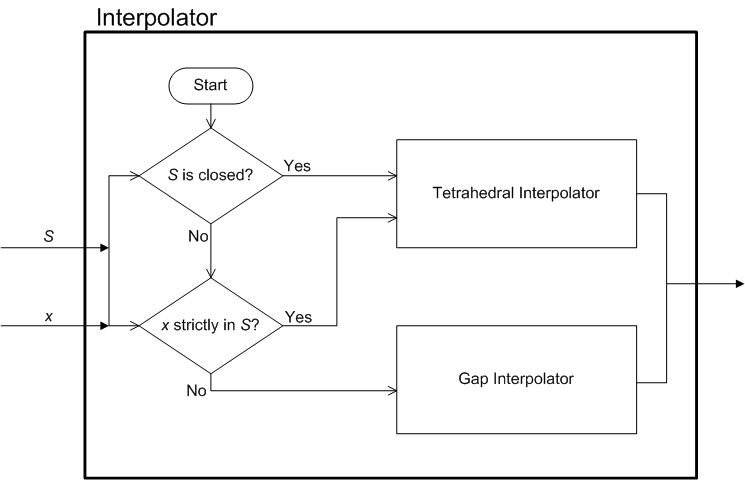
Diagrama que muestra la parte dos de la arquitectura del módulo de interpolación.

Figura 1: Arquitectura del módulo de interpolación

Como se explicó anteriormente, este algoritmo puede lograr un muestreo razonablemente denso en las regiones del espacio del dispositivo que contienen una combinación importante de colorantes, a la vez que minimiza el tamaño total de las LUT necesarias. En la tabla siguiente se muestra una comparación del número de nodos necesarios para la implementación dispersa de LUT (mediante algoritmo #1 y modo normal) y la implementación uniforme de LUT correspondiente.

Número de canales de entrada	LUT dispersa	LUT uniforme
5	142498	1419857
6	217582	24137567
7	347444	410338673
8	559618	6975757441

Interpolación dentro de un cubo de unidad

Un paso básico en el caso de la cuadrícula rectangular es la interpolación dentro de una celda envolvente. Para un punto de entrada, puede determinar fácilmente la celda envolvente. En una cuadrícula rectangular, se especifica el valor de salida en cada uno de los vértices (puntos de esquina) de la celda envolvente. También son las únicas condiciones de límite (NIC) que debe cumplir un interpolante: el interpolante debe pasar por todos estos puntos. Tenga en cuenta que estas condiciones de límite están en puntos "discretos", en este caso los 2n puntos de esquina de la celda, donde n es la dimensión del espacio de color.

Es útil formalizar el concepto de condiciones de límite antes de continuar. Para cualquier subconjunto S del límite de la celda envolvente (el cubo de unidad en n dimensiones), una condición de límite en S es una especificación de una función BC: S → Rm, donde m es la dimensión de salida. Es decir, se requiere un interpolante, que puede indicarse Interp: [0,1]n→ Rm, para satisfacer: Interp(x) = BC(x) para todas las x en S.

En el escenario estándar de interpolación en el cubo de unidad, S es el conjunto de puntos discretos que son los 2n vértices del cubo.

Ahora puede generalizar las condiciones de límite para resolver los problemas descritos anteriormente y proporcionar un nuevo algoritmo de interpolación dentro del cubo de unidad. En lugar de permitir solo puntos de límite discretos, las condiciones de límite se pueden imponer en una cara de límite completa del cubo. Las suposiciones precisas son las siguientes:

(a) El punto vn =(1,1,...,1) es especial y solo se permite una condición de límite discreta. En otras palabras, no se pueden imponer condiciones de límite continuo en las n caras de límite xi=1 (i=1,...,n).

(b) Para cada uno de los n límites restantes caras xi=0 (i=1,...,n), la condición de límite se puede imponer en toda la cara, con la condición de compatibilidad que, si dos caras se intersecan, las condiciones de límite de las caras deben aceptar la intersección.

(c) Los vértices no contenidos en las caras con condición de límite tendrán una condición de límite individual (discreta).

Puede hacer referencia a una condición de límite discreta como datos finitos y una condición de límite continuo como datos transfinidos para analizar la interpolación de datos finitos y transfinidos.

En primer lugar, revise la interpolación tetrahedral estándar (como la utilizada en la patente de Sakamoto) que ayuda a establecer las notaciones para esta formulación concreta del problema. Se sabe que el cubo de unidad [0,1]n se puede subdividir en n! tetrahedra, parametrizada por el conjunto de permutaciones en n símbolos. Más concretamente, cada uno de estos tetrahedrones se define por desigualdades

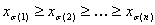
Muestra la fórmula de las desigualdades de los tetrahedrones.

donde σ:{1,2,..,n}→{1,2,...,n} es una permutación de "símbolos" 1, 2, ..., n, es decir, es una asignación bijetiva del conjunto de n símbolos. Por ejemplo, si n = 3 y σ = (3, 2, 1), lo que significa σ(1)=3, σ(2)=2, σ(3)=1, entonces el tetraedron correspondiente se define mediante z≥y≥x, donde se usa la notación común x, y, z para x1, x2, x3. Tenga en cuenta que estos tetrahedrones no están separados entre sí. Para la interpolación, los puntos que se basan en una cara común de dos tetraedrones distintos tendrán el mismo valor de interpolación independientemente de qué tetrahedron se use en la interpolación. Aun así, en el escenario estándar de interpolación en puntos finitos, para un punto de entrada determinado (x1, ..., xn), primero determine en qué tetrahedron se encuentra, o equivalentemente, la permutación correspondiente σ, el interpolador tetrahedral se define como

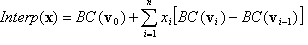
Muestra la ecuación que define el interpolante tetrahedral.

donde 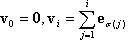Muestra la ecuación para los vectores de base estándar. para i=1, ..., n y e1, ..., son los vectores de base estándar. Antes de pasar a la generalización, tenga en cuenta que v0, v1, ..., vn son los vértices del tetrahedro y 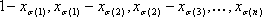Muestra las coordenadas barícéntricas. son las "coordenadas barycéntricas".

Para el caso general de los BCs en caras de límite, puede usar el concepto de proyección barycéntrica. Como antes, para un punto de entrada determinado (x1, ..., xn), primero determine en qué tetraedro se encuentra, o equivalentemente, la permutación correspondiente σ. A continuación, realice una serie de proyecciones barycéntricas, como se indica a continuación. La primera proyección 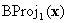muestra el subíndice BProj 1 (x). envía el punto al plano 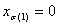Muestra la diferencia de subíndice X (1) igual a 0. a menos que 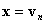Muestra X igual a V subíndice n. en cuyo caso no se cambia. La definición precisa del mapa BProj se define de la siguiente manera:

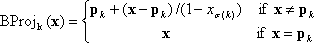
Muestra la ecuación para la definición precisa del mapa BProj.

con 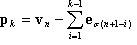Muestra la ecuación para el subíndice P k. y k = 1, 2, ..., n.

En el caso 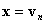Muestra X es igual a V subíndice n. , puede detener, ya que BC se define en vn por Suposición (a). En el caso 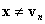Muestra X no es igual a V subíndice n. , es claro que 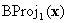muestra el subíndice BProj 1 (X). tiene el componente σ(1) annihilado. En otras palabras, se encuentra en una de las caras de límite. Está en una cara en la que se define BC, en cuyo caso puede detener o realizar otra proyección barycéntrica 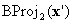muestra el subíndice BProj 2 (X'). 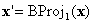donde muestra X' igual a BProj subíndice 1 (X). . 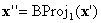Y si muestra X''= subíndice Bproj 1 (X'). está en una cara en la que se define BC, puede detener; De lo contrario, realice otra proyección 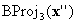muestra el subíndice BProj 3 (X'). . Dado que cada proyección elimina un componente, la dimensión efectiva disminuye, por lo que sabe que el proceso debe detenerse finalmente. En el peor de los casos, se realizan n proyecciones hasta la dimensión 0, es decir, vértices en el cubo, que según suposición (c), sabe que BC se definirá.

Suponiendo que se han realizado proyecciones K, con

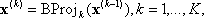
Muestra una ecuación para usar suponiendo que se ha realizado la proyección K.

x(0)= x, el punto de entrada y BC se define en x(k). A continuación, desenrede las proyecciones definiendo una serie de vectores de salida:

Muestra ecuaciones para una serie de vectores de salida.

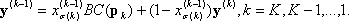
donde 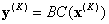Muestra la ecuación para superíndice Y (K). y, por último, obtiene la respuesta.

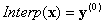
Muestra interp(x) igual a y superíndice (0).

Ejemplo de trabajo

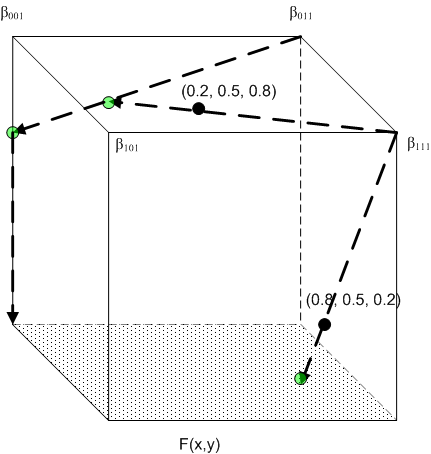
Diagrama que muestra un ejemplo trabajado de interpolación con un cubo de unidad.

Figura 2: ejemplo de Trabajo

Tenga en cuenta la situación que se muestra en la figura 2, donde n = 3, m = 1 y tiene las siguientes NIC:

(a) Cuatro BC discretos en los vértices

(0, 0, 1): β001

(0, 1, 1): β011

(1, 0, 1): β101

(1, 1, 1): β111

(b) Un BC continuo en la cara x3=0: F(x1, x2)

Cálculo n.º 1: punto de entrada x = (0,8, 0,5, 0,2). El tetraedro envolvente está asociado a la permutación <1, 2, 3>.

1ª proyección: 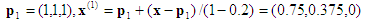Muestra la ecuación de la primera proyección.

Esto ya está en la cara x3=0, por lo que puede detener. Después, la sustitución hacia atrás da

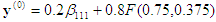Muestra la respuesta de la primera proyección. que es la respuesta.

Cálculo n.º 2: punto de entrada x = (0,2, 0,5, 0,8). El tetraedro envolvente está asociado a la permutación <3, 2, 1>.

1ª proyección: 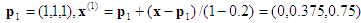Muestra la ecuación para la primera proyección del cálculo 2.

2ª proyección: 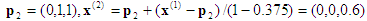Muestra la ecuación para la segunda proyección del cálculo 2.

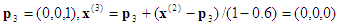Tercera proyección: Muestra la ecuación para la tercera proyección del cálculo 2. , que se encuentra en la cara x3=0. Después, la sustitución hacia atrás da

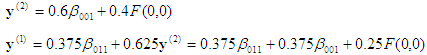
Muestra las dos primeras ecuaciones para la sustitución hacia atrás.

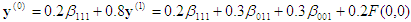Muestra la tercera ecuación para la sustitución hacia atrás. , que es la respuesta final.

Aplicaciones

(a) Interpolación tetrahedral secuencial

Diagrama que muestra la interpolación tetrahedral secuencial.

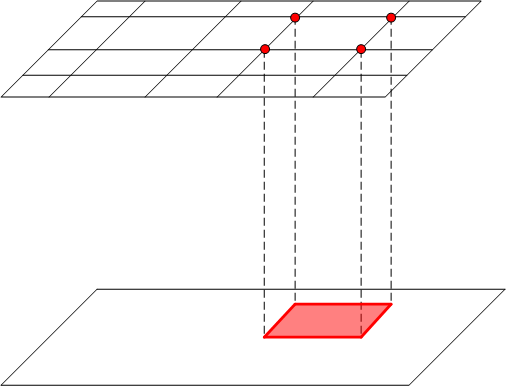
Figura 3: interpolación tetrahedral secuencial

Consulte la figura 3. Para interpolar entre dos planos en los que se han impuesto cuadrículas incompatibles, considere la posibilidad de incluir una celda que incluya un punto determinado P que se muestra en la figura. Los vértices "top" de la celda proceden directamente de la cuadrícula del plano superior. Los vértices de la cara inferior no son compatibles con la cuadrícula del plano inferior, por lo que toda la cara se trata como una BC con valores obtenidos por interpolación en la cuadrícula del plano inferior. A continuación, queda claro que esta configuración satisface las suposiciones (a), (b) y (c) anteriores, y puede aplicar el algoritmo de interpolación.

También es evidente que el algoritmo ha reducido la dimensión del problema de interpolación en 1, ya que el resultado es una combinación lineal de valores en los vértices de la cuadrícula superior y la interpolación en el plano inferior, que tiene la dimensión menos 1. Si existe una configuración de plano de sándwich similar en el plano inferior, puede aplicar el procedimiento en ese plano, lo que reduce aún más la dimensión en 1. Este procedimiento puede continuar hasta alcanzar la dimensión 0. Esta cascada de proyecciones e interpolaciones se puede llamar "Interpolación tetrahedral secuencial".

(b) de interpolación de brechas

Diagrama que muestra la interpolación de brechas.

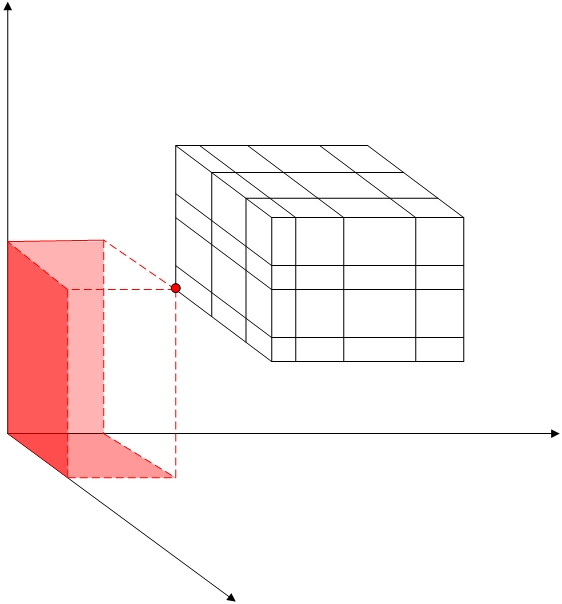
Figura 4: interpolación de brechas de

Se trata de una cuadrícula impuesta a un cubo que se encuentra estrictamente dentro del cuadrante positivo. El propio cubo tiene una cuadrícula en ella y cada plano de coordenadas tiene cuadrículas que no son necesariamente compatibles. La "brecha" entre el cubo y los planos de coordenadas tiene una sección transversal que es "con forma L" y no es amenable para las técnicas estándar. Sin embargo, con la técnica introducida aquí, puede introducir fácilmente celdas que cubran esta brecha. En la figura 4 se muestra una de estas. Las cuadrículas de los planos de coordenadas admiten la interpolación que proporciona los BCs necesarios para todas las caras inferiores de la celda, con un vértice restante cuyo BC es proporcionado por la esquina inferior del cubo.

Nota final sobre la implementación

En la aplicación real, el "cubo de unidad" que es el valor básico del algoritmo se extrae de lasttices más grandes y los valores de los vértices pueden requerir un cálculo costoso. Por otro lado, también está claro que la interpolación tetrahedral solo requiere los valores en los vértices del tetrahedro, que es un subconjunto de todos los vértices del cubo de unidad. Por lo tanto, es más eficaz implementar lo que se puede denominar "evaluación diferida". En una implementación de software del algoritmo anterior, es habitual tener una subrutina que toma el cubo de unidad y los valores en sus vértices como entrada. La evaluación diferida significa que, en lugar de pasar los valores en los vértices, se pasa la información necesaria para evaluar los valores de los vértices, sin llevar a cabo realmente la evaluación. Dentro de la subrutina, la evaluación real de estos valores solo se llevará a cabo para los vértices que pertenecen al tetraedro envolvente, después de determinar el tetrahedron envolvente.

Tabla de búsqueda para su uso con dispositivos de origen RGB virtual de alto rango dinámico

En el caso de que una transformación se construya con un dispositivo de origen que se modele como un dispositivo RGB virtual, es posible que los valores de colorante de origen sean negativos o mayores que unity (1.0). Cuando esto ocurre, el dispositivo de origen se conoce como tener un rango dinámico alto (HDR). Se hace especial consideración para este caso.

En el caso de las transformaciones HDR, los valores mínimo y máximo de cada canal de color se pueden determinar a partir del límite de gama del dispositivo. Al usar estos valores, se aplica un escalado simple para cada canal de color para que los valores de coloreado iguales al color mínimo se conviertan en 0,0 y los valores de colorante iguales al colorante máximo se convertirán en 1,0, con un escalado lineal de valores entre para asignar linealmente entre 0,0 y 1,0.

ICCProfileFromWCSProfile

Dado que el propósito principal de esta característica es admitir versiones anteriores a Vista de Windows, debe generar perfiles ICC de la versión 2.2 tal como se define en la especificación ICC.1:1998-09. En determinados casos (vea la siguiente tabla "Baseline Device To ICC Profile Class Mapping"), puede crear una matriz o un perfil de ICC basado en TRC a partir de un perfil wcS. En otros casos, el perfil icc consta de LUT. En el proceso siguiente se describe cómo crear las LUT AToB y BToA. Por supuesto, los perfiles icc también tienen otros campos. Algunos de los datos se pueden derivar del perfil de WCS. Para otros datos, tendrá que desarrollar valores predeterminados inteligentes. Los derechos de autor se asignarán a Microsoft; puesto que es tecnología de Microsoft que se usa para crear las LUT.

Este diseño debe funcionar para todos los tipos de modelos de dispositivo, incluidos los complementos. Siempre que el complemento tenga un modelo de dispositivo de línea base asociado, se puede determinar el tipo de dispositivo subyacente.

La parte difícil de crear un perfil icc es crear las tablas de búsqueda AToB y BToA. Estas tablas se asignan entre el espacio del dispositivo, por ejemplo, RGB o CMYK, y el espacio de conexión de perfil (PCS), que es una variante de CIELAB. Esto es fundamentalmente lo mismo que el proceso de administración de colores usado en la transformación CITE para asignar desde el espacio del dispositivo al espacio del dispositivo. Sin embargo, debe tener la siguiente información para realizar la transformación.

Condiciones de visualización de referencia para pcS.
Gama de PCS de referencia.
Modelo de dispositivo que convierte entre los valores de PCS y la colorimetría.

El perfil de WCS y su CAM asociado se proporcionan como parámetros. Hay dos modelos de dispositivo de línea base que convierten entre colorimetría y la codificación PCS. La razón por la que necesita dos se explica a continuación.

Puede obtener las condiciones de visualización de referencia para el PCS a partir de la especificación de formato de perfil ICC. La información proporcionada en la especificación del formato de perfil ICC es suficiente para calcular todos los datos necesarios para inicializar la CAM utilizada por el CMS. Para lograr coherencia y flexibilidad, esta información se almacena en un perfil de color WCS.
También puede usar un perfil de WCS para almacenar ejemplos que definen la gama de referencias del PCS. El sistema de administración de colores CITE (CMS) tiene dos maneras de crear límites de gama. Una consiste en muestrear el espacio completo del dispositivo y usar el modelo de dispositivo para crear valores de medida. El segundo método consiste en usar ejemplos medidos del perfil para crear un límite de gama de referencia. Dado que la gama del PCS de la ICC es demasiado grande para hacer una gama de referencia útil, el primer método es inapropiado. Pero el segundo método es un enfoque flexible basado en perfiles. Para redefinir la gama de PCS de referencia, puede cambiar los datos de medida en el perfil del dispositivo PCS.
El PCS ICC es un modelado de un dispositivo ideal. Al crear un modelo de PCS como un dispositivo real, puede aprovechar el proceso de administración de colores usado en Smart CMM. Crear un modelo de dispositivo a partir de colorimetry a la codificación PCS es sencillo. Simplemente se asigna entre los valores colorimétricos verdaderos y los valores codificados por PCS. Dado que la interfaz CMS para los modelos de dispositivo solo admite valores XYZ, es posible que también tenga que asignar entre XYZ y LAB. Se trata de una transformación conocida. Este modelo se describe en el documento 2.2.02 "Modelos de dispositivo de línea base" en las secciones 7.9 y 7.10.

Es posible que tenga que realizar alguna asignación de la gama, si la gama del dispositivo es mayor que la gama del PCS. Los GMM de línea base se pueden usar para este fin. Tenga en cuenta que un perfil ICC creado correctamente tiene tablas de búsqueda para las intenciones Relativas Colorimétrica, Perceptual y Saturación, aunque pueden apuntar a la misma LUT internamente.

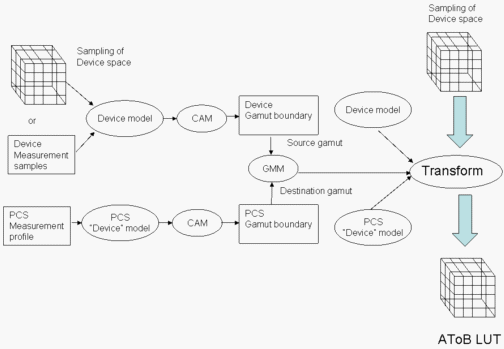Diagrama que muestra la creación de un A T O B L U.

Figura 5: creación de un LUT de AToB

Este proceso se muestra en la figura 5. En primer lugar, el modelo de dispositivo se inicializa a partir de los datos del perfil de DM. A continuación, cree un límite de gama de dispositivos como se indica a continuación. Un muestreo de datos del modelo de dispositivo se ejecuta a través del modelo de dispositivo para obtener datos colorimétricos. Los datos colorimétricos se ejecutan a través del CAM para crear datos de apariencia. Los datos de apariencia se usan para crear el límite de gama del dispositivo.

A continuación, use los datos del perfil de medición de PCS de referencia para crear un límite de gama para el PCS.

Use los dos límites de gama que acaba de crear para inicializar un GMM. A continuación, use el modelo de dispositivo, el GMM y el modelo de dispositivo PCS para crear una transformación. Ejecute un muestreo del espacio del dispositivo a través de la transformación para crear una LUT de AToB.

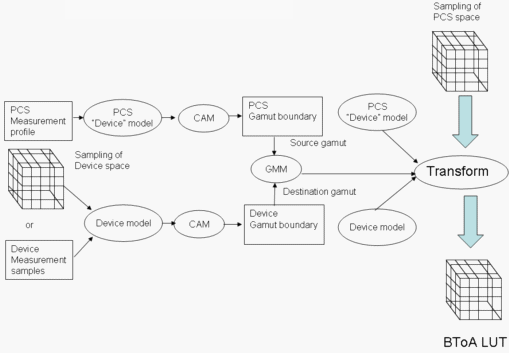
Diagrama que muestra la creación de un T o B L U T mediante un muestreo del espacio de P C S.

Figura 6: creación de un LUT BToA

En la figura 6 se muestra la creación del LUT BToA. Esto es casi idéntico a la creación de una LUT de AToB, con los roles de origen y destino intercambiados. Además, debe muestrear la gama completa de PCS para crear la LUT.

Tenga en cuenta que, dado que la CAM (CIECAM02 en WCS) está implicada en el proceso, la adaptación cromática entre el punto blanco multimedia y el punto blanco pcS (ordenado por la ICC para que sea el de D50) se aplica de forma transparente por la CAM.

Dispositivos RGB virtuales HDR

Se debe tener especial consideración al generar perfiles para dispositivos RGB virtuales HDR; es decir, los dispositivos para los que los valores de color pueden ser inferiores a 0,0 o mayores que 1,0. En la generación de la LUT ATOB, se crea un conjunto mayor de LUT de entrada 1D. Los valores de coloración se escalan y se desplazan al intervalo 0 . 1 usando los valores mínimos y máximos de color en el perfil de WCS.

Dado que es probable que el espacio de color para dispositivos HDR no se rellene completamente, también se proporciona compatibilidad especial en el LUT 3D para la etiqueta. Para controlar los colores en la región rellenada dispersamente, los colorantes se recodrán para que se pueda lograr la extrapolación más allá de 0,0 y 1,0. El intervalo usado es -1 .. +4.

Debido a la reasignación aplicada para el LUT 3D, se crea un conjunto de LUT de salida 1D para asignar el resultado al intervalo 0 . 1.

Más de un PCS

La ICC constató que un PCS no era suficientemente flexible para cumplir todos los usos previstos de un CMS. En la versión 4 de la especificación de perfil, el ICC aclaró que en realidad hay dos codificaciones PCS. Se usa uno para las intenciones colorimétricas; otro se usa para la intención perceptual. (No se especifica ningún PCS para la intención saturación. La ICC ha dejado esta parte ambigua. El PCS colorimétrico tiene una ligereza mínima y máxima especificada, pero los valores cromáticos y de matiz oscilan aproximadamente ± 127. Este PCS se parece a un prisma rectangular. Como se mencionó anteriormente, el volumen de PCS perceptual es similar a la gama de una impresora de inyección de lápiz.

Los dos PCS icc también tienen dos codificaciones digitales diferentes. En el PCS perceptual, un valor de cero representa una ligereza de cero. En el PCS colorimétrico, un valor de cero representa la ligereza mínima del PCS, que es mayor que cero. Puede resolver este problema teniendo un modelo de dispositivo diferente para cada una de las codificaciones pcS.

Asignación de gamut

Para crear las LUT de AToB en un perfil icc, se asigna desde la gama de dispositivos al espacio pcS adecuado. Para crear las LUT de BToA, se asigna desde el espacio pcS a la gama de dispositivos. La asignación de los LUT de AToB es bastante similar a la usada en un CMS basado en medidas. Para los PCS perceptuales, asigne la gama factible del dispositivo al límite de la gama de PCS perceptual, usando recortes o compresión para los colores fuera de la gama. Para las intenciones colorimétricas, es posible que tenga que recortar la luz, pero todos los valores cromáticos y de matiz van a caber en la gama PCS colorimétrica.

La asignación de luT de BToA es un poco diferente. Las intenciones colorimétricas siguen siendo fáciles; solo tiene que recortar los valores de PCS en la gama de dispositivos. Pero la ICC requiere que todos los valores pcS posibles se asignen a algún valor de dispositivo, no solo los que se encuentran dentro de la gama de referencia de los PCS perceptuales. Por lo tanto, debe asegurarse de que los GMM pueden controlar los colores de origen que están fuera de la gama de referencia. Esto se puede controlar recortando esos colores al límite de la gama del dispositivo.

Asignación de clases de perfil icc de dispositivo de línea base a ICC

Tipo de dispositivo de línea base	Clase de perfil ICC	Comentario
Dispositivo de captura RGB	Dispositivo de entrada ("scnr")	PCS es CIELAB. AToB0Tag es Device to PCS con la intención colorimétrica relativa.
CRT, monitor LCD	Dispositivo para mostrar ("mntr")	PCS es CIEXYZ. Consulte lo siguiente para la conversión de modelos.
Proyector RGB	Espacio de color ("espaciado")	PCS es CIELAB.
Impresora RGB y CMYK	Dispositivo de salida ("prtr")	PCS es CIELAB.
Dispositivo virtual RGB (mayúsculas y minúsculas no HDR)	Dispositivo para mostrar ("mntr")	PCS es CIEXYZ.
Dispositivo virtual RGB (caso HDR)	Espacio de color ("espaciado")	PCS es CIELAB.

La conversión de perfiles de supervisión no implica la creación de LUT, sino que consiste en crear una matriz o un modelo de TRC. El modelo utilizado en ICC es ligeramente diferente del utilizado en el modelado CRT o LCD de WCS en que falta el término "corrección negra". Específicamente

Modelo WCS: 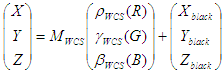Muestra un modelo de W C S.

Modelo ICC: 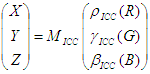muestra un modelo de C C.

La conversión del modelo WCS al modelo ICC se realiza de la siguiente manera.

Definir nuevas curvas:

Muestra una matriz para definir nuevas curvas.

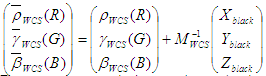
Estas no son curvas de reproducción de tono porque no asignan 1 a 1. Una normalización logrará eso. Las definiciones finales del modelo de la ICC son:

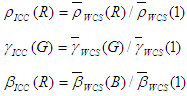
Muestra las definiciones finales del modelo de C de I.

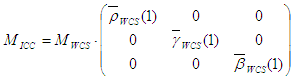
Muestra la matriz final del modelo de C de I.

En el caso de los dispositivos virtuales RGB que no son HDR, también está generando un perfil icc para mostrar para la eficiencia del espacio. En ese caso, la matriz tristimulus M ICC se puede obtener directamente de las principales del perfil wcS sin la conversión del modelo anterior. Una matriz final, pero importante, es que esta matriz tristimulus debe adaptarse cromáticamente a D50 para cumplir con la especificación ICC del PCS. Es decir, las entradas de cada fila de la matriz que se van a codificar en el perfil ICC deben sumar respectivamente a 96.42, 100 y 82.49. En la implementación actual, la adaptación cromática se realiza mediante CAT02, que también es la transformación de adaptación cromática utilizada en CAM02.

Conservación negra y generación negra

La implementación de conservación negra está vinculada con la generación del canal negro en dispositivos que admiten un canal negro. Para ello, se recopila información sobre cada color de origen para permitir que los modelos de dispositivo que admitan un canal negro determinen cómo establecer mejor el canal negro en la salida. Aunque la conservación negra es pertinente para las transformaciones de color que se convierten entre un dispositivo de canal negro a otro, la generación negra se implementa para todas las transformaciones que implican un dispositivo de destino de canal negro.

La información del canal negro se registra en una estructura de datos denominada BlackInformation. La estructura BlackInformation contiene un booleano que indica si el color contiene solo color negro y un valor numérico que indica el grado de "negro" denominado peso negro. En el caso de los dispositivos de origen que admiten un canal negro, el peso negro es el porcentaje de color negro en el color de origen. En el caso de los dispositivos de origen que no contienen un canal negro, el peso negro se calcula mediante los demás colorantes y el valor de apariencia. Se calcula un valor denominado "pureza de color" tomando la diferencia entre el valor de color máximo y el valor de color mínimo dividido por el valor de color máximo. Se calcula un valor denominado "ligereza relativa" tomando la diferencia entre la ligereza del color y la ligereza mínima para el dispositivo de destino dividida por la diferencia entre la ligereza mínima y máxima del dispositivo de destino. Si el dispositivo de origen es un dispositivo aditivo (monitor o proyector), el peso negro se determina que es el 1,0 menos la pureza de color multiplicada por la ligereza relativa. Por ejemplo, si el dispositivo de origen es un monitor RGB, se calcula el valor máximo y el valor mínimo de R, G y B para cada color y la fórmula determina el peso negro:

BW = (1.0 – (max(R,G,B) – min(R,G,B)) / max(R, G, B)) * luz relativa

Si el dispositivo de origen admite la coloración resta, por ejemplo, una impresora CMY, los coloradores individuales deben ser "uno complementado" (restado de 1,0) antes de usarlo en la fórmula anterior. Por lo tanto, para una impresora CMY, R = 1,0 – C, G = 1,0 – M y B = 1,0 – Y.

La información negra de cada color procesada por la transformación de color se determina durante el proceso de traducción de colores. La información de solo negro solo se determina si se especifica conservación negra. El peso negro siempre se determina si el modelo de dispositivo de destino admite un color negro. La información negra se pasa al modelo de dispositivo de destino a través del método ColorimetricToDeviceColorsWithBlack, que usa la LUT resultante.

Tenga en cuenta que, debido a la optimización de la transformación de color, el proceso anterior solo se produce durante la creación de la transformación optimizada LUT, no durante la ejecución del método TranslateColors.

Optimización para transformaciones con más de tres canales de origen

El tamaño de la transformación optimizada viene determinado por varios factores: el número de canales de color en el dispositivo de origen, el número de pasos de la tabla para cada canal de color de origen y el número de canales de color en el dispositivo de salida. La fórmula para determinar el tamaño de la tabla de transformación es:

Tamaño = Número de pasos por canal _{origen\ dispositivo(Número\ de\ canales\ in\ source\device)} x número de canales en el dispositivo de salida

Como puede ver, el tamaño de la tabla crece exponencialmente en función del número de canales del dispositivo de origen. Muchos dispositivos de origen admiten tres canales de color, por ejemplo, Rojo, Verde y Azul. Sin embargo, si un dispositivo de origen admite cuatro canales, como CMYK, el tamaño de la tabla y el tiempo necesario para construir la tabla crecen por un factor del número de pasos. En un CMS basado en medidas en el que las transformaciones se construyen "sobre la marcha", esta vez puede ser aceptable.

Para reducir el tiempo necesario para construir la tabla de conversión de colores, es posible aprovechar dos hechos. En primer lugar, aunque el dispositivo de origen puede admitir más de tres canales de color, el espacio de color intermedio independiente del dispositivo (CIECAM02 Ja _C b _C ) tiene solo tres canales de color. En segundo lugar, la parte más lenta del procesamiento no es el modelado de dispositivos (conversión de coordenadas de color del dispositivo a valores tristimulus), pero la asignación de la gama. Con estos hechos, puede construir una tabla de conversión de colores preliminar que convierta los colores en el espacio de colores independiente del dispositivo a través de los pasos de asignación de la gama y, por último, a través del modelo de color del dispositivo de salida. La construcción de esta tabla es de la dimensión tres. A continuación, creamos la tabla de conversión de color final de la dimensión cuatro convirtiendo las combinaciones de colores de origen en espacio intermedio independiente del dispositivo y, a continuación, usando la tabla preliminar de conversión de colores, finaliza la conversión al espacio de colores del dispositivo de salida. Por lo tanto, se reduce la computación (número de pasos de la tabla de búsqueda) _{número\ de canales\} cálculos de asignación de la mutación al número de pasos de la tabla intermedia ₃ cálculos de asignación de la mutación. Aunque tiene que realizar un número de pasos en la (tabla de búsqueda) _{número\ de canales\} cálculos de modelado de dispositivos y búsquedas de tablas tridimensionales, esto sigue siendo mucho más rápido que el cálculo original.

El proceso anterior funcionará bien siempre que no sea necesario que la información pase entre el modelo de dispositivo de origen y cualquier otro componente de la transformación de color. Sin embargo, si el dispositivo de salida y el dispositivo de origen admiten un color negro y el color negro de origen se usa para determinar el color negro de salida, el proceso no podrá comunicar correctamente la información negra de origen. Un proceso alternativo consiste en construir una tabla de conversión de colores preliminar que convierta los colores en el espacio de colores independiente del dispositivo solo a través de los pasos de asignación de la gama. A continuación, construya la tabla de conversión de color final de la dimensión cuatro mediante los pasos siguientes: a) convierta las combinaciones de colores de origen en el espacio independiente del dispositivo intermedio, b) realice los pasos de asignación de la mutación mediante la interpolación en la tabla de colores preliminar en lugar de aplicar los procesos de asignación de la gama real y c) use los valores resultantes de los pasos de asignación de la gama y cualquier información del canal negro de origen para calcular los colorantes del dispositivo de salida mediante el modelo de dispositivo de salida. Este proceso también se puede usar cuando hay información transferida entre los modelos de dispositivo de origen y salida incluso si no hay ningún canal negro; Por ejemplo, si los dos módulos se implementan con una arquitectura de complemento que permite el intercambio de datos entre módulos.

Los dos procesos anteriores se pueden usar para mejorar eficazmente el tiempo necesario para construir la tabla de transformación de colores de cuatro dimensiones.

CheckGamut

El ICM llama a CreateTransform y CreateMultiProfileTransform tomar una palabra de valores de marca, uno de los cuales es ENABLE_GAMUT_CHECKING. Cuando se establece esta marca, CITE debe crear la transformación de forma diferente. Los pasos iniciales son los mismos: se deben inicializar las CAM de origen y destino y, a continuación, se deben inicializar los descriptores de límite de gama de origen y destino. Independientemente de la intención especificada, se debe usar checkGamut GMM. El GMM checkGamut debe inicializarse mediante los modelos de dispositivo de origen y destino y los descriptores de límite de gama. Sin embargo, la transformación debe crear una transformación truncada que comprende el modelo de dispositivo de origen, el CAM de origen, los GMM intermedios y checkGamut GMM. Esto garantiza que los valores delta J, delta C y delta h generados por checkGamut CMM se convierten en los valores resultantes finales.

El significado de CheckGamut está claro cuando solo hay dos perfiles de dispositivo en la transformación. Cuando hay más de dos perfiles de dispositivo y más de dos GMM, CheckGamut notifica si los colores que se han transformado a través del primer modelo de dispositivo y todos los GMM, pero el último GMM se encuentra dentro de la gama del dispositivo de destino.

conceptos básicos de administración de colores
esquemas y algoritmos del sistema de colores de Windows

Compartir a través de