Tres tipos de curvas de Bézier
Explorar cómo usar SkiaSharp para representar curvas de Bézier cúbicas, cuadráticas y cónicas
La curva de Bézier lleva el nombre en honor a Pierre Bézier (1910–1999), ingeniero francés de la compañía automotriz Renault que usó la curva para el diseño asistido por ordenador de los cuerpos de los automóviles.
Las curvas de Bézier son conocidas por ser adecuadas para el diseño interactivo: se comportan bien (es decir, no hay singularidades que hacen que la curva se convierta en infinita o incomoda) y, por lo general, tienen una estética agradable:

Los contornos de caracteres de las fuentes basadas en equipos normalmente se definen con curvas de Bézier.
El artículo de Wikipedia sobre la curva de Bézier contiene información general útil. El término curva de Bézier realmente hace referencia a una familia de curvas similares. SkiaSharp admite tres tipos de curvas de Bézier, denominadas cúbicas, cuadráticas y cónicas. La cónica también se conoce como cuadrática racional.
Curva de Bézier cúbica
El cúbica es el tipo de curva de Bézier en el que piensa la mayoría de los desarrolladores cuando surge el tema de las curvas de Bézier.
Puede agregar una curva de Bézier cúbica a un SKPath objeto mediante el método de CubicTo con tres parámetros SKPoint o la sobrecarga CubicTo con parámetros independientes x y y:
public void CubicTo (SKPoint point1, SKPoint point2, SKPoint point3)
public void CubicTo (Single x1, Single y1, Single x2, Single y2, Single x3, Single y3)
La curva comienza en el punto actual del contorno. La curva de Bezier cúbica completa se define mediante cuatro puntos:
- punto inicial: punto actual en el contorno o (0, 0) si no se ha llamado a
MoveTo - primer punto de control:
point1en la llamadaCubicTo - segundo punto de control:
point2en la llamadaCubicTo - punto final:
point3en la llamadaCubicTo
La curva resultante comienza en el punto inicial y termina en el punto final. Normalmente la curva no pasa por los dos puntos de control. En lugar de eso, los puntos de control funcionan de forma muy similar a los imanes para extraer la curva hacia ellos.
La mejor manera de sentir la curva de Bézier cúbica es experimentando. Este es el propósito de la curva de Bézier, que deriva de InteractivePage. El archivo BezierCurvePage.xaml crea una instancia del SKCanvasView y de un TouchEffect. El archivo de código subyacente BezierCurvePage.xaml.cs crea cuatro objetos TouchPoint en su constructor. El controlador de eventos PaintSurface crea un SKPath para representar una curva de Bézier basada en los cuatro objetos TouchPoint y también dibuja líneas tangentes punteadas desde los puntos de control hasta los puntos finales:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with cubic Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.CubicTo(touchPoints[1].Center,
touchPoints[2].Center,
touchPoints[3].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[2].Center.X,
touchPoints[2].Center.Y,
touchPoints[3].Center.X,
touchPoints[3].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
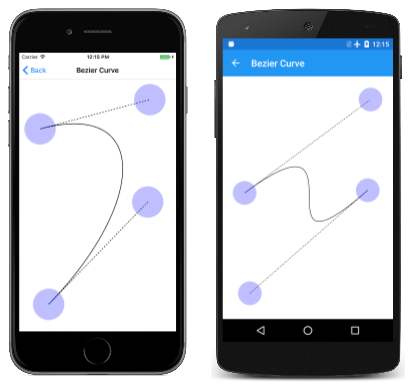
Aquí se está ejecutando:
Matemáticamente, la curva es un polinomial cúbico. La curva interseca una línea recta en tres puntos como máximo. En el punto inicial la curva siempre es tangente a una línea recta desde el punto inicial hasta el primer punto de control y tiene la misma dirección. En el punto final la curva siempre es tangente a una línea recta desde el segundo punto de control hasta el punto final y tiene la misma dirección que.
La curva de Bézier cúbica siempre está limitada por un cuadrilátero convexo que conecta los cuatro puntos. Se denomina casco convexo. Si los puntos de control se encuentran en la línea recta entre el punto inicial y el final, la curva de Bézier se representa como una línea recta. Pero la curva también puede cruzarse a sí misma, tal y como se muestra en la tercera captura de pantalla.
Un contorno de trazado puede contener varias curvas de Bézier cúbicas conectadas, pero la conexión entre dos solo será suave si los tres puntos siguientes son colineales, es decir, se encuentran en una línea recta:
- segundo punto de control de la curva
- el punto final de la primera curva, que también es el punto inicial de la segunda curva
- primer punto de control de la segunda curva
En el siguiente artículo sobre los datos de rutas SVG, descubrirá una instalación para facilitar la definición de curvas de Bézier conectadas suaves.
A veces resulta útil conocer las ecuaciones paramétricas subyacentes que representan una curva de Bézier cúbica. Para t comprendido entre 0 y 1, las ecuaciones paramétricas son las siguientes:
x(t) = (1 – t)³x₀ + 3t(1 – t)²x₁ + 3t²(1 – t)x₂ + t³x₃
y(t) = (1 – t)³y₀ + 3t(1 – t)²y₁ + 3t²(1 – t)y₂ + t³y₃
El exponente más alto de 3 confirma que son polinomiales cúbicos. Es fácil comprobar que cuando t es igual a 0, el punto es (x₀, y₀), que es el punto inicial, y cuando t es igual a 1, el punto es (x₃, y₃), que es el punto final. Cerca del punto inicial (para valores bajos de t), el primer punto de control (x₁, y₁) tiene un efecto fuerte, y cerca del punto final (valores altos de 't') el segundo punto de control (x₂, y₂) tiene un efecto fuerte.
Aproximación de una curva de Bézier a arcos circulares
A veces es conveniente usar una curva de Bézier para representar un arco circular. Una curva cúbica de Bézier puede aproximarse muy bien a un arco circular hasta el círculo de un cuarto, por lo que cuatro curvas Bézier conectadas pueden definir un círculo entero. Esta aproximación se analiza en dos artículos publicados hace más de 25 años:
Tor Dokken, et a "Good Approximation of Circles by Curvature-Continuous Bézier curves,"l (Buena aproximación de círculos mediante curvas de Bézier de curvatura continua), Computer Aided Geometric Design 7 (Diseño geométrico asistido por ordenador 7) (1990), 33-41.
Michael Goldapp, "Approximation of Circular Arcs by Cubic Polynomials" (Aproximación de arcos circulares mediante polinomiales cúbicos), Computer Aided Geometric Design 8 (Diseño geométrico asistido por ordenador 8) (1991), 227-238.
En el diagrama siguiente se muestran cuatro puntos con las etiquetas pto, pt1, pt2 y pt3 que definen una curva de Bézier (que se muestra en rojo) que se aproxima a un arco circular:
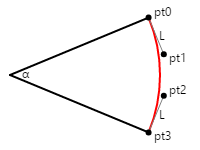
Las líneas que van de los puntos inicial y final a los puntos de control son tangentes al círculo y a la curva de Bézier, y tienen una longitud de L. En el primer artículo mencionado anteriormente, se indica que la curva de Bézier se aproxima mejor a un arco circular cuando esa longitud L se calcula de la siguiente manera:
L = 4 × tan(α / 4) / 3
La ilustración muestra un ángulo de 45 grados, por lo que L es igual a 0,265. En el código, ese valor se multiplicaría por el radio deseado del círculo.
La página Bezier Circular Arc permite experimentar con la definición de una curva de Bézier para aproximar un arco circular para ángulos de hasta 180 grados. El archivo BezierCircularArcPage.xaml crea una instancia del SKCanvasView y de un Slider para seleccionar el ángulo. El controlador de eventos PaintSurface del archivo de código subyacente BezierCircularArgPage.xaml.cs usa una transformación para establecer el punto (0, 0) en el centro del lienzo. Dibuja un círculo centrado en ese punto para la comparación y, a continuación, calcula los dos puntos de control de la curva de Bézier:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 3;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate length of control point line
float length = radius * 4 * (float)Math.Tan(Math.PI * angle / 180 / 4) / 3;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the end points
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point3 = new SKPoint(radius * sin, radius * cos);
// Find the control points
SKPoint point0Normalized = Normalize(point0);
SKPoint point1 = point0 + new SKPoint(length * point0Normalized.Y,
-length * point0Normalized.X);
SKPoint point3Normalized = Normalize(point3);
SKPoint point2 = point3 + new SKPoint(-length * point3Normalized.Y,
length * point3Normalized.X);
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
canvas.DrawCircle(point3.X, point3.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point3.X, point3.Y, point2.X, point2.Y, dottedStroke);
// Draw the Bezier curve
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.CubicTo(point1, point2, point3);
canvas.DrawPath(path, redStroke);
}
}
// Vector methods
SKPoint Normalize(SKPoint v)
{
float magnitude = Magnitude(v);
return new SKPoint(v.X / magnitude, v.Y / magnitude);
}
float Magnitude(SKPoint v)
{
return (float)Math.Sqrt(v.X * v.X + v.Y * v.Y);
}
Los puntos inicial y final (point0 y point3) se calculan en función de las ecuaciones paramétricas normales del círculo. Dado que el círculo se centra en (0, 0), estos puntos también se pueden tratar como vectores radiales desde el centro del círculo hasta la circunferencia. Los puntos de control están en líneas que son tangentes al círculo, por lo que están en ángulos rectos a estos vectores radiales. Un vector en ángulo derecho a otro es simplemente el vector original con las coordenadas X e Y intercambiadas y una de ellas negativa.
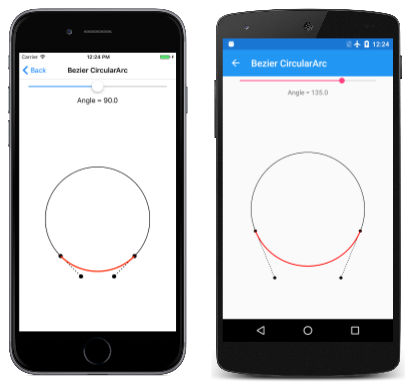
Este es el programa que se ejecuta con diferentes ángulos:
Observe detenidamente la tercera captura de pantalla y verá que la curva de Bézier se desvía notablemente de un semicírculo cuando el ángulo es de 180 grados, pero la pantalla de iOS muestra que parece ajustarse a un círculo de un cuarto justo cuando el ángulo es de 90 grados.
Calcular las coordenadas de los dos puntos de control es bastante fácil cuando el círculo del cuarto está orientado de esta manera:
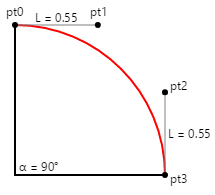
Si el radio del círculo es 100, L es 55, un número fácil de recordar.
La página Squaring the Circle (Cálculo de la raíz cuadrada del círculo) anima una figura entre un círculo y un cuadrado. Al círculo se aproximan cuatro curvas de Bézier cuyas coordenadas se muestran en la primera columna de esta definición de matriz de la clase SquaringTheCirclePage:
public class SquaringTheCirclePage : ContentPage
{
SKPoint[,] points =
{
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() },
{ new SKPoint( 55, 100), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 55), new SKPoint( 62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 100, 0), new SKPoint( 125, 0), new SKPoint() },
{ new SKPoint( 100, -55), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 55, -100), new SKPoint( 62.5f, -62.5f), new SKPoint() },
{ new SKPoint( 0, -100), new SKPoint( 0, -125), new SKPoint() },
{ new SKPoint( -55, -100), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, -55), new SKPoint(-62.5f, -62.5f), new SKPoint() },
{ new SKPoint(-100, 0), new SKPoint( -125, 0), new SKPoint() },
{ new SKPoint(-100, 55), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( -55, 100), new SKPoint(-62.5f, 62.5f), new SKPoint() },
{ new SKPoint( 0, 100), new SKPoint( 0, 125), new SKPoint() }
};
...
}
La segunda columna contiene las coordenadas de cuatro curvas de Bézier que definen un cuadrado cuyo área es aproximadamente la misma que el área del círculo. (Dibujar un cuadrado con el área exacta de la de un determinado círculo es el clásico problema geométrico sin solución de calcular la raíz cuadrada del círculo.) Para representar un cuadrado con curvas de Bézier, los dos puntos de control de cada curva son los mismos y son colineales con los puntos inicial y final, por lo que la curva de Bézier se representa como una línea recta.
La tercera columna de la matriz es para los valores interpolados de una animación. La página establece un temporizador de 16 milisegundos y se llama al controlador PaintSurface a esa velocidad:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(Math.Min(info.Width / 300, info.Height / 300));
// Interpolate
TimeSpan timeSpan = new TimeSpan(DateTime.Now.Ticks);
float t = (float)(timeSpan.TotalSeconds % 3 / 3); // 0 to 1 every 3 seconds
t = (1 + (float)Math.Sin(2 * Math.PI * t)) / 2; // 0 to 1 to 0 sinusoidally
for (int i = 0; i < 13; i++)
{
points[i, 2] = new SKPoint(
(1 - t) * points[i, 0].X + t * points[i, 1].X,
(1 - t) * points[i, 0].Y + t * points[i, 1].Y);
}
// Create the path and draw it
using (SKPath path = new SKPath())
{
path.MoveTo(points[0, 2]);
for (int i = 1; i < 13; i += 3)
{
path.CubicTo(points[i, 2], points[i + 1, 2], points[i + 2, 2]);
}
path.Close();
canvas.DrawPath(path, cyanFill);
canvas.DrawPath(path, blueStroke);
}
}
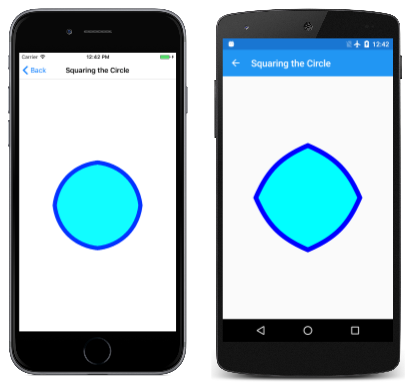
Los puntos se interpolan en función de un valor oscilante sinusoide de t. Los puntos interpolados se usan para construir una serie de cuatro curvas de Bézier conectadas. A continuación se muestra la animación en ejecución:
Esta animación sería imposible sin curvas que fuesen lo suficientemente flexibles algorítmicamente hablando como para representarse como arcos circulares y líneas rectas.
La página Bezier Infinity también aprovecha la capacidad de una curva de Bézier para aproximarse a un arco circular. Este es el controlador PaintSurface de la clase BezierInfinityPage:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
using (SKPath path = new SKPath())
{
path.MoveTo(0, 0); // Center
path.CubicTo( 50, -50, 95, -100, 150, -100); // To top of right loop
path.CubicTo( 205, -100, 250, -55, 250, 0); // To far right of right loop
path.CubicTo( 250, 55, 205, 100, 150, 100); // To bottom of right loop
path.CubicTo( 95, 100, 50, 50, 0, 0); // Back to center
path.CubicTo( -50, -50, -95, -100, -150, -100); // To top of left loop
path.CubicTo(-205, -100, -250, -55, -250, 0); // To far left of left loop
path.CubicTo(-250, 55, -205, 100, -150, 100); // To bottom of left loop
path.CubicTo( -95, 100, -50, 50, 0, 0); // Back to center
path.Close();
SKRect pathBounds = path.Bounds;
canvas.Translate(info.Width / 2, info.Height / 2);
canvas.Scale(0.9f * Math.Min(info.Width / pathBounds.Width,
info.Height / pathBounds.Height));
using (SKPaint paint = new SKPaint())
{
paint.Style = SKPaintStyle.Stroke;
paint.Color = SKColors.Blue;
paint.StrokeWidth = 5;
canvas.DrawPath(path, paint);
}
}
}
Puede ser un buen ejercicio trazar estas coordenadas en el grafo para ver cómo están relacionadas. El signo infinito se centra alrededor del punto (0, 0) y los dos bucles tienen centros de (–150, 0) y (150, 0) y radii de 100. En la serie de comandos CubicTo, puede ver las coordenadas X de los puntos de control que toman valores de –95 y –205 (esos valores son –150 más y menos 55), 205 y 95 (150 más y menos 55), así como 250 y –250 para los lados derecho e izquierdo. La única excepción es cuando el signo infinito se cruza en el centro. En ese caso, los puntos de control tienen coordenadas con una combinación de 50 y –50 para enderezar la curva cerca del centro.
Este es el signo infinito:
Es algo más suave hacia el centro que el signo infinito representado por la página Arc Infinity del artículo Three Ways to Draw an Arc (Tres formas de dibujar un arco).
Curva de Bézier cuadrática
La curva de Bézier cuadrática tiene solo un punto de control y la curva se define por solo tres puntos: el punto inicial, el punto de control y el punto final. Las ecuaciones paramétricas son muy similares a la curva de Bézier cúbica, salvo que el exponente más alto es 2, por lo que la curva es un polinomial cuadrático:
x(t) = (1 – t)²x₀ + 2t(1 – t)x₁ + t²x₂
y(t) = (1 – t)²y₀ + 2t(1 – t)y₁ + t²y₂
Para agregar una curva de Bézier cuadrática a una ruta de acceso, use el método QuadTo o la sobrecarga QuadTo con coordenadas independientes x y y:
public void QuadTo (SKPoint point1, SKPoint point2)
public void QuadTo (Single x1, Single y1, Single x2, Single y2)
Los métodos agregan una curva de la posición actual a point2 con point1 como punto de control.
Puede experimentar con curvas de Bézier cuadráticas mediante la página Curva cuadrática, que es muy similar a la página Curva de Bézier, excepto que solo tiene tres puntos táctiles. Este es el controlador PaintSurface del archivo de código subyacente QuadraticCurve.xaml.cs:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with quadratic Bezier
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.QuadTo(touchPoints[1].Center,
touchPoints[2].Center);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
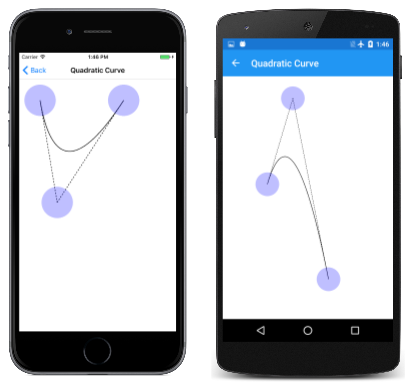
Aquí se está ejecutando:
Las líneas de puntos son tangentes a la curva en el punto inicial y el punto final, y se reúnen en el punto de control.
El Bézier cuadrático es bueno si necesita una curva de una forma general, pero prefiere la comodidad de solo un punto de control en lugar de dos. El Bézier cuadrático se representa de forma más eficaz que cualquier otra curva, por lo que se usa internamente en Skia para representar arcos elípticos.
Sin embargo, la forma de una curva de Bézier cuadrática no es elíptica, por lo que se requieren varios Bézier cuadráticos para aproximarse a un arco elíptico. En lugar de eso el Bézier cuadrático es un segmento de una parábola.
Curva de Bézier cónica
La curva de Bézier cónica, también conocida como curva de Bézier cuadrática racional, es una suma relativamente reciente a la familia de curvas de Bézier. Al igual que la curva de Bézier cuadrática, la curva de Bézier cuadrática racional implica un punto inicial, un punto de conexión y un punto de control. Pero la curva de Bézier cuadrática racional también requiere un valor de peso. Se denomina cuadrática racional porque las fórmulas paramétricas implican relaciones.
Las ecuaciones paramétricas para X e Y son ratios que comparten el mismo denominador. Esta es la ecuación del denominador para t comprendido entre 0 y 1 y un valor de peso de w:
d(t) = (1 – t)² + 2wt(1 – t) + t²
En teoría, un cuadrático racional puede implicar tres valores de peso independientes, uno para cada uno de los tres términos, pero estos se pueden simplificar a un solo valor de peso en el término medio.
Las ecuaciones paramétricas de las coordenadas X e Y son similares a las ecuaciones paramétricas del Bézier cuadrático, salvo que el término medio también incluye el valor de peso y la expresión se divide por el denominador:
x(t) = ((1 – t)²x₀ + 2wt(1 – t)x₁ + t²x₂)) ÷ d(t)
y(t) = ((1 – t)²y₀ + 2wt(1 – t)y₁ + t²y₂)) ÷ d(t)
Las curvas de Bézier cuadráticas racionales también se denominan cónicas porque pueden representar exactamente segmentos de cualquier sección cónica: hipérbolas, parábolas, elipses y círculos.
Para agregar una curva de Bézier cuadrática a una ruta de acceso, use el método ConicTo o la sobrecarga ConicTo con coordenadas independientes x y y:
public void ConicTo (SKPoint point1, SKPoint point2, Single weight)
public void ConicTo (Single x1, Single y1, Single x2, Single y2, Single weight)
Observe el parámetro final weight.
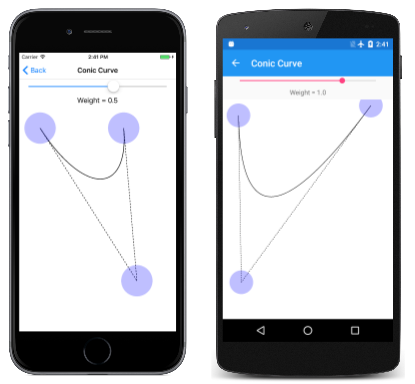
La página Curva cónica permite experimentar con estas curvas. La clase ConicCurvePage deriva de InteractivePage. El archivo ConicCurvePage.xaml crea una instancia de un Slider para seleccionar un valor de peso entre –2 y 2. El archivo de código subyacente ConicCurvePage.xaml.cs crea tres objetos TouchPoint y el controlador PaintSurface simplemente representa la curva resultante con las líneas tangentes a los puntos de control:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Draw path with conic curve
using (SKPath path = new SKPath())
{
path.MoveTo(touchPoints[0].Center);
path.ConicTo(touchPoints[1].Center,
touchPoints[2].Center,
(float)weightSlider.Value);
canvas.DrawPath(path, strokePaint);
}
// Draw tangent lines
canvas.DrawLine(touchPoints[0].Center.X,
touchPoints[0].Center.Y,
touchPoints[1].Center.X,
touchPoints[1].Center.Y, dottedStrokePaint);
canvas.DrawLine(touchPoints[1].Center.X,
touchPoints[1].Center.Y,
touchPoints[2].Center.X,
touchPoints[2].Center.Y, dottedStrokePaint);
foreach (TouchPoint touchPoint in touchPoints)
{
touchPoint.Paint(canvas);
}
}
Aquí se está ejecutando:
Como puede ver, el punto de control parece extraer la curva hacia ella más cuando el peso es mayor. Cuando el peso es cero, la curva se convierte en una línea recta desde el punto inicial hasta el punto final.
En teoría, se permiten pesos negativos y hacen que la curva se aleje del punto de control. Sin embargo, los pesos de –1 o inferiores hacen que el denominador de las ecuaciones paramétricas se convierta en negativo para determinados valores de t. Probablemente por este motivo, los pesos negativos se omiten en los métodos ConicTo. El programa Curva cónica le permite establecer pesos negativos, pero como puede ver experimentando, los pesos negativos tienen el mismo efecto que un peso de cero y hacen que se represente una línea recta.
Es muy fácil derivar el punto de control y el peso para usar el método ConicTo con el fin de dibujar un arco circular de hasta un semicírculo, pero no incluido. En el diagrama siguiente, las líneas tangentes de los puntos inicial y final se encuentran en el punto de control.
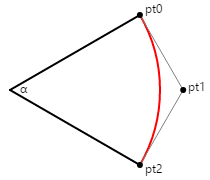
Puede usar trigonometría para determinar la distancia del punto de control desde el centro del círculo: es el radio del círculo dividido por el coseno de la mitad del ángulo α. Para dibujar un arco circular entre los puntos inicial y final, establezca el peso en ese mismo coseno de la mitad del ángulo. Observe que si el ángulo es de 180 grados, las líneas tangentes nunca se encuentran y el peso es cero. En el caso de los ángulos inferiores a 180 grados, sirven las matemáticas.
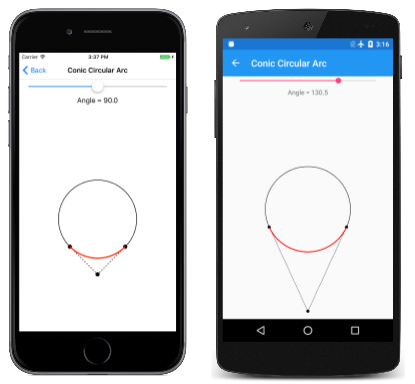
En la página Arco circular cónico se muestra esto. El archivo ConicCircularArc.xaml crea una instancia de un Slider para seleccionar el ángulo. El controlador PaintSurface del archivo de código subyacente ConicCircularArc.xaml.cs calcula el punto de control y el peso:
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Translate to center
canvas.Translate(info.Width / 2, info.Height / 2);
// Draw the circle
float radius = Math.Min(info.Width, info.Height) / 4;
canvas.DrawCircle(0, 0, radius, blackStroke);
// Get the value of the Slider
float angle = (float)angleSlider.Value;
// Calculate sin and cosine for half that angle
float sin = (float)Math.Sin(Math.PI * angle / 180 / 2);
float cos = (float)Math.Cos(Math.PI * angle / 180 / 2);
// Find the points and weight
SKPoint point0 = new SKPoint(-radius * sin, radius * cos);
SKPoint point1 = new SKPoint(0, radius / cos);
SKPoint point2 = new SKPoint(radius * sin, radius * cos);
float weight = cos;
// Draw the points
canvas.DrawCircle(point0.X, point0.Y, 10, blackFill);
canvas.DrawCircle(point1.X, point1.Y, 10, blackFill);
canvas.DrawCircle(point2.X, point2.Y, 10, blackFill);
// Draw the tangent lines
canvas.DrawLine(point0.X, point0.Y, point1.X, point1.Y, dottedStroke);
canvas.DrawLine(point2.X, point2.Y, point1.X, point1.Y, dottedStroke);
// Draw the conic
using (SKPath path = new SKPath())
{
path.MoveTo(point0);
path.ConicTo(point1, point2, weight);
canvas.DrawPath(path, redStroke);
}
}
Como puede ver, no hay ninguna diferencia visual entre la ruta de acceso ConicTo que se muestra en rojo y el círculo subyacente que se muestra como referencia:
Pero establezca el ángulo en 180 grados, entonces las matemáticas fallan.
Es una pena ver que en este caso ConicTo no admite pesos negativos, porque en teoría (basado en las ecuaciones paramétricas), el círculo se puede completar con otra llamada a ConicTo con los mismos puntos, pero un valor negativo del peso. Esto permitiría crear un círculo entero con solo dos curvas ConicTo basadas en cualquier ángulo entre cero grados y 180 grados, no incluidos.
 Descargar el ejemplo
Descargar el ejemplo