Métriques d’évaluation pour les modèles d’analyses de texte personnalisées pour l’intégrité
Votre jeu de données est divisé en deux parties : un jeu pour l’entraînement et un jeu pour le test. Le jeu d’entraînement est utilisé pour entraîner le modèle, tandis que le jeu de tests est utilisé comme test pour le modèle après l’entraînement pour calculer les performances et l’évaluation du modèle. Le jeu de tests n’est pas introduit dans le modèle via le processus de formation afin de s’assurer que le modèle est testé sur de nouvelles données.
L’évaluation du modèle est déclenchée automatiquement une fois l’entraînement effectué. Le processus d’évaluation commence par l’utilisation du modèle entraîné pour prédire les entités définies par l’utilisateur pour les documents du jeu de test. Il les compare aux étiquettes de données fournies (ce qui établit une base de référence de confiance). Les résultats sont retournés pour pouvoir examiner les performances du modèle. Les entités définies par l’utilisateur sont incluses dans la prise en compte de l’évaluation des composants Learned et List. Les entités prédéfinies d’analyses de texte pour l’intégrité ne sont pas prises en compte dans l’évaluation du modèle. Pour l’évaluation, les analyses de texte personnalisées pour l’intégrité utilisent les métriques suivantes :
Précision : mesure la précision/justesse de votre modèle. Il s’agit du rapport entre les positifs correctement identifiés (vrais positifs) et tous les positifs identifiés. La métrique de précision révèle le nombre d’entités prédites qui sont correctement étiquetées.
Precision = #True_Positive / (#True_Positive + #False_Positive)Rappel : mesure la capacité du modèle à prédire les classes positives réelles. Il s’agit du rapport entre les vrais positifs prédits et ce qui a été réellement étiqueté. La métrique de rappel révèle le nombre d’entités prédites correctes.
Recall = #True_Positive / (#True_Positive + #False_Negatives)Score F1 : le score F1 est une fonction de précision et de rappel. Il est nécessaire quand vous recherchez l’équilibre entre précision et rappel.
F1 Score = 2 * Precision * Recall / (Precision + Recall)
Notes
La précision, le rappel et le score F1 sont calculés séparément pour chaque entité (évaluation au niveau de l’entité) et collectivement pour le modèle (évaluation au niveau du modèle).
Métriques d’évaluation au niveau du modèle et au niveau de l’entité
La précision, le rappel et le score F1 sont calculés séparément pour chaque entité (évaluation au niveau de l’entité) et collectivement pour le modèle (évaluation au niveau du modèle).
Les définitions de la précision, du rappel et de l’évaluation sont les mêmes pour les évaluations au niveau de l’entité et au niveau du modèle. Toutefois, le nombre de vrais positifs, faux positifs et faux négatifs peut différer. Par exemple, prenons le texte suivant.
Exemple
La première partie dans ce contrat est John Smith, résidant au 5678 Main Rd., ville de Frederick, État du Nebraska. Et la deuxième partie est Forrest Ray, résidant au 123-345 Integer Rd., ville de Corona, État du Nouveau-Mexique. Il y a également Fannie Thomas résidant au 7890 River Road, ville de Colorado Springs, État du Colorado.
Le modèle qui extrait les entités de ce texte peut avoir les prédictions suivantes :
| Entité | Prédiction effectuée sous forme de | Type réel |
|---|---|---|
| John Smith | Personne | Personne |
| Frederick | Personne | City |
| Forrest | City | Personne |
| Fannie Thomas | Personne | Personne |
| Colorado Springs | City | City |
Évaluation au niveau de l’entité pour l’entité personne
Le modèle comporte l’évaluation au niveau de l’entité suivante, pour l’entité personne :
| Clé | Count | Explication |
|---|---|---|
| Vrai positif | 2 | John Smith et Fannie Thomas ont été correctement prédits en tant que Personne. |
| Faux positif | 1 | Frederick a été prédit de manière incorrecte en tant que Personne alors qu’il s’agit d’une Ville. |
| Faux négatif | 1 | Forrest a été prédit à tort en tant que ville alors qu’il aurait dû s’agir d’une personne. |
- Précision :
#True_Positive / (#True_Positive + #False_Positive)=2 / (2 + 1) = 0.67 - Rappel :
#True_Positive / (#True_Positive + #False_Negatives)=2 / (2 + 1) = 0.67 - Score F1 :
2 * Precision * Recall / (Precision + Recall)=(2 * 0.67 * 0.67) / (0.67 + 0.67) = 0.67
Évaluation au niveau de l’entité pour l’entité ville
Le modèle comporte l’évaluation au niveau de l’entité suivante, pour l’entité ville :
| Clé | Count | Explication |
|---|---|---|
| Vrai positif | 1 | Colorado Springs a été correctement prédit en tant que ville. |
| Faux positif | 1 | Forrest a été prédit de manière incorrecte en tant que Ville alors qu’il s’agit d’une Personne. |
| Faux négatif | 1 | Frederick a été prédit de manière incorrecte en tant que Personne alors qu’il s’agit d’une Ville. |
- Précision =
#True_Positive / (#True_Positive + #False_Positive)=1 / (1 + 1) = 0.5 - Rappel =
#True_Positive / (#True_Positive + #False_Negatives)=1 / (1 + 1) = 0.5 - Score F1 =
2 * Precision * Recall / (Precision + Recall)=(2 * 0.5 * 0.5) / (0.5 + 0.5) = 0.5
Évaluation au niveau du modèle pour le modèle collectif
Le modèle comporte l’évaluation suivante pour le modèle dans son intégralité :
| Clé | Count | Explication |
|---|---|---|
| Vrai positif | 3 | John Smith et Fannie Thomas ont été correctement prédits en tant que Personne. Colorado Springs a été prédit correctement en tant que Ville. Il s’agit de la somme des vrais positifs pour toutes les entités. |
| Faux positif | 2 | Forrest a été prédit de manière incorrecte en tant que Ville alors qu’il s’agit d’une Personne. Frederick a été prédit de manière incorrecte en tant que Personne alors qu’il s’agit d’une Ville. Il s’agit de la somme des faux positifs pour toutes les entités. |
| Faux négatif | 2 | Forrest a été prédit de manière incorrecte en tant que Ville alors qu’il s’agit d’une Personne. Frederick a été prédit de manière incorrecte en tant que Personne alors qu’il s’agit d’une Ville. Il s’agit de la somme des faux négatifs pour toutes les entités. |
- Précision =
#True_Positive / (#True_Positive + #False_Positive)=3 / (3 + 2) = 0.6 - Rappel =
#True_Positive / (#True_Positive + #False_Negatives)=3 / (3 + 2) = 0.6 - Score F1 =
2 * Precision * Recall / (Precision + Recall)=(2 * 0.6 * 0.6) / (0.6 + 0.6) = 0.6
Interprétation des métriques d’évaluation au niveau de l’entité
Que signifie réellement avoir une précision élevée ou un rappel élevé pour une certaine entité ?
| Rappel | Precision | Interprétation |
|---|---|---|
| Élevé | Élevé | Cette entité est correctement gérée par le modèle. |
| Faible | Élevé | Le modèle ne peut pas toujours extraire cette entité, mais quand le cas se présente, il le fait avec un niveau de confiance élevé. |
| Élevé | Faible | Le modèle extrait correctement cette entité, mais son niveau de confiance est faible, car l’entité est parfois extraite sous un autre type. |
| Faible | Faible | Ce type d’entité est mal géré par le modèle, car il n’est généralement pas extrait. Quand le cas se présente, le niveau de confiance n’est pas élevé. |
Assistance
Après avoir formé votre modèle, vous verrez des conseils et des recommandations sur la façon d’améliorer le modèle. Il est recommandé d’avoir un modèle couvrant tous les points de la section conseils.
Le jeu d’entraînement contient suffisamment de données : lorsqu’un type d’entité a moins de 15 instances étiquetées dans les données d’apprentissage, il peut entraîner une précision inférieure en raison du fait que le modèle n’est pas correctement formé sur ces cas. Dans ce cas, envisagez d’ajouter d’autres données étiquetées dans le jeu d’entraînement. Vous pouvez consulter l’onglet Distribution des données pour obtenir d’autres conseils.
Tous les types d’entités sont présents dans le jeu de tests : lorsque les données de test manquent d’instances étiquetées pour un type d’entité, les performances de test du modèle peuvent devenir moins complètes en raison de scénarios non testés. Vous pouvez consulter l’onglet Distribution des données de jeu de test pour obtenir d’autres conseils.
Les types d’entités sont équilibrés dans les jeux d’apprentissage et de test : lorsque le biais d’échantillonnage provoque une représentation inexacte de la fréquence d’un type d’entité, il peut entraîner une précision inférieure en raison du modèle qui s’attend à ce que ce type d’entité se produise trop souvent ou trop peu. Vous pouvez consulter l’onglet Distribution des données pour obtenir d’autres conseils.
Les types d’entités sont distribués uniformément entre les jeux d’apprentissage et de test : lorsque le mélange de types d’entités ne correspond pas entre les jeux d’entraînement et de test, il peut entraîner une précision de test inférieure en raison de l’apprentissage du modèle différemment de la façon dont il est testé. Vous pouvez consulter l’onglet Distribution des données pour obtenir d’autres conseils.
Distinction peu claire entre les types d’entités dans le jeu d’entraînement : lorsque les données d’apprentissage sont similaires pour plusieurs types d’entités, cela peut entraîner une précision inférieure, car les types d’entités peuvent être fréquemment mal classés les uns comme les autres. Passez en revue les types d’entités suivants et envisagez de les fusionner s’ils sont similaires. Sinon, ajoutez d’autres exemples pour mieux les distinguer les uns des autres. Vous pouvez consulter l’onglet Matrice de confusion pour obtenir des conseils supplémentaires.
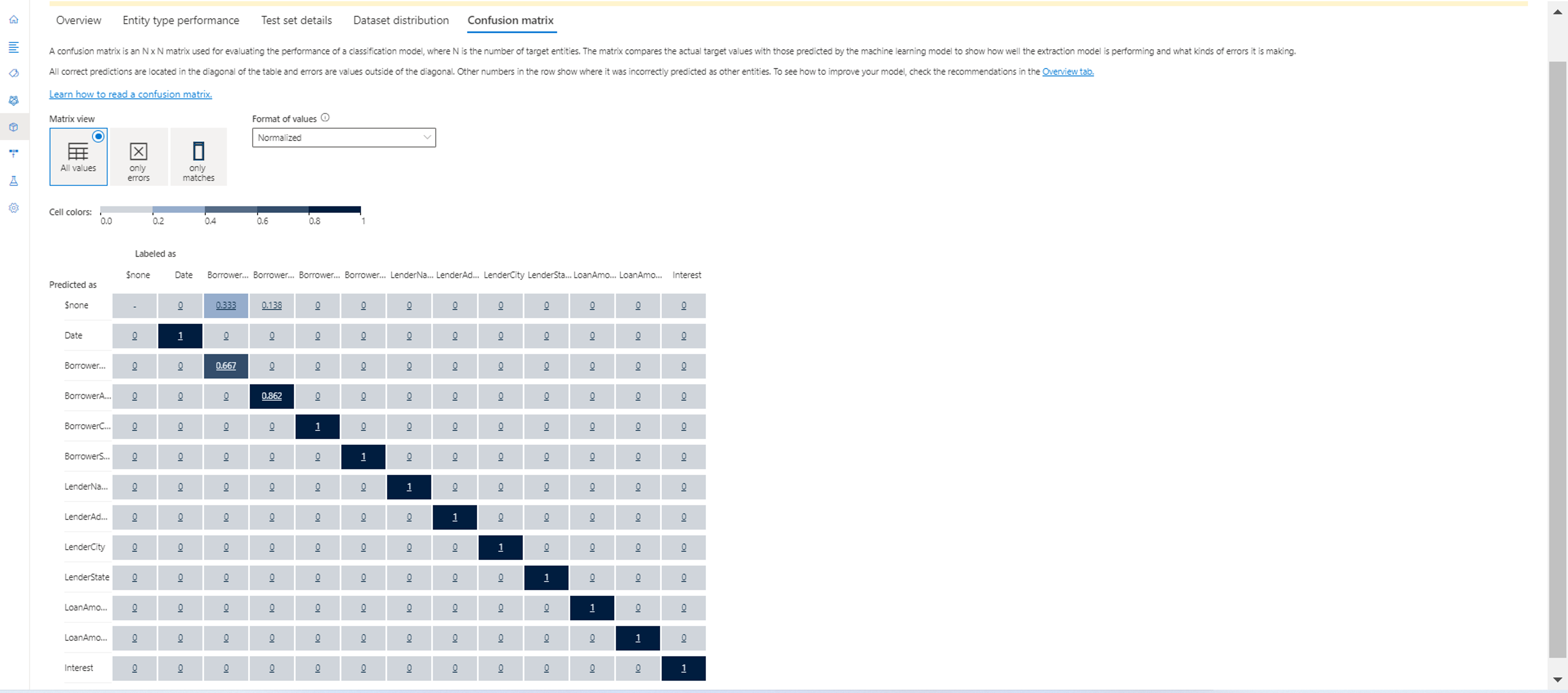
Matrice de confusion
Une matrice de confusion est une matrice N x N utilisée pour l’évaluation des performances du modèle, N étant le nombre d’entités. La matrice compare les étiquettes attendues aux étiquettes prédites par le modèle. Cela donne une vue holistique du niveau de performance du modèle et des genres d’erreur qu’il commet.
Vous pouvez utiliser la matrice de confusion pour identifier les entités trop proches les unes des autres et qui sont souvent mal interprétées (ambiguïté). Dans ce cas, fusionnez ces types d’entité. Si cela n’est pas possible, ajoutez d’autres exemples étiquetés des deux entités pour permettre au modèle de les différencier.
La diagonale en surbrillance dans l’image ci-dessous correspond aux entités correctement prédites, où l’étiquette prédite est la même que l’étiquette réelle.
Vous pouvez calculer les métriques d’évaluation au niveau de l’entité et au niveau du modèle à partir de la matrice de confusion :
- Les valeurs de la diagonale sont les valeurs correspondant aux vrais positifs de chaque entité.
- La somme des valeurs des lignes d’entité (à l’exception de la diagonale) correspond au faux positif du modèle.
- La somme des valeurs des colonnes d’entité (à l’exception de la diagonale) correspond au faux négatif du modèle.
De même,
- Le vrai positif du modèle correspond à la somme des vrais positifs de toutes les entités.
- Le faux positif du modèle correspond à la somme des faux positifs de toutes les entités.
- Le faux négatif du modèle correspond à la somme des faux négatifs de toutes les entités.