Hash Join
When it comes to physical join operators, hash join does the heavy lifting. While nested loops join works well with relatively small data sets and merge join helps with moderately sized data sets, hash join excels at performing the largest joins. Hash joins parallelize and scale better than any other join and are great at maximizing throughput in data warehouses. (I’ll discuss parallel query execution in future series of posts.)
Hash join shares many characteristics with merge join. Like merge join, it requires at least one equijoin predicate, supports residual predicates, and supports all outer and semi-joins. Unlike merge join, it does not require ordered input sets and, while it does support full outer join, it does require an equijoin predicate.
The algorithm
The hash join executes in two phases: build and probe. During the build phase, it reads all rows from the first input (often called the left or build input), hashes the rows on the equijoin keys, and creates an in-memory hash table. During the probe phase, it reads all rows from the second input (often called the right or probe input), hashes these rows on the same equijoin keys, and looks or probes for matching rows in the hash table. Since hash functions can lead to collisions (two different key values that hash to the same value), we typically must check each potential match to ensure that it really joins.
In pseudo-code:
for each row R1 in the build table
begin
calculate hash value on R1 join key(s)
insert R1 into the appropriate hash bucket
end
for each row R2 in the probe table
begin
calculate hash value on R2 join key(s)
for each row R1 in the corresponding hash bucket
if R1 joins with R2
return (R1, R2)
end
Note that unlike the nested loops and merge joins which immediately begin flowing output rows, the hash join is blocking on its build input. That is, it must completely read and process its entire build input before it can return any rows. Moreover, unlike the other join methods, the hash join requires a memory grant to store the hash table. Thus, there is a limit to the number of concurrent hash joins that SQL Server can run at any given time. While these characteristics are generally not a problem for data warehouses, they are undesirable for most OLTP applications.
Memory and spilling
Before a hash join begins execution, SQL Server tries to estimate how much memory it will need to build its hash table. We use the cardinality estimate for the size of the build input along with the expected average row size to estimate the memory requirement. To minimize the memory required by the hash join, we try to choose the smaller of the two tables as the build table. We then try to reserve this much memory to ensure that the hash join can successfully execute.
What happens if we grant the hash join less memory than it requests or if the estimate is too low? In these cases, the hash join may run out of memory during the build phase. If the hash join runs out of memory, it begins spilling a small percentage of the total hash table to disk (to a workfile in tempdb). The hash join keeps track of which “partitions” of the hash table are still in memory and which ones have been spilled to disk. As we read each new row from the build table, we check to see whether it hashes to an in-memory or an on-disk partition. If it hashes to an in-memory partition, we proceed normally. If it hashes to an on-disk partition, we write the row to disk. This process of running out of memory and spilling partitions to disk may repeat multiple times until the build phase is complete.
We perform a similar process during the probe phase. For each new row from the probe table, we check to see whether it hashes to an in-memory or an on-disk partition. If it hashes to an in-memory partition, we probe the hash table, produce any appropriate joined rows, and discard the row. If it hashes to an on-disk partition, we write the row to disk. Once we complete the first pass of the probe table, we return one by one to any partitions that we spilled, read the build rows back into memory, reconstruct the hash table for each partition, and then read the corresponding probe partitions and complete the join.
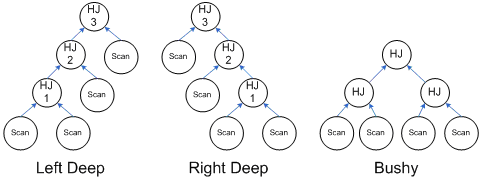
Left deep vs. right deep vs. bushy hash join trees
These terms refer to the shape of the query plan as illustrated by this figure:
The shape of the join tree is particularly interesting for hash joins as it affects the memory consumption.
In a left deep tree, the output of one hash join is the build input to the next hash join. Because hash joins consume their entire build input before moving to the probe phase, in a left deep tree only adjacent pairs of hash joins are active at the same time. For example, in the above picture, we begin by building the hash table for HJ1. When HJ1 begins probing, we use the output of HJ1 to build the hash table for HJ2. When HJ1 is done probing, we can release the memory used by its hash table. Only then do we begin probing HJ2 and building the hash table for HJ3. Thus, HJ1 and HJ3 are never active at the same time and can share the same memory grant. The total amount of memory we need is max(HJ1 + HJ2, HJ2 + HJ3).
In a right deep tree, the output of one hash join is the probe input to the next hash join. All of the hash joins must build their complete hash tables before we can begin probing. All of the hash joins are active at once and cannot share memory. When we do begin probing, rows flow up the entire tree of hash joins without blocking. Thus, the total amount of memory we need is HJ1 + HJ2 + HJ3.
Examples
The following examples use this schema:
create table T1 (a int, b int, x char(200))
create table T2 (a int, b int, x char(200))
create table T3 (a int, b int, x char(200))
set nocount on
declare @i int
set @i = 0
while @i < 1000
begin
insert T1 values (@i * 2, @i * 5, @i)
set @i = @i + 1
end
declare @i int
set @i = 0
while @i < 10000
begin
insert T2 values (@i * 3, @i * 7, @i)
set @i = @i + 1
end
declare @i int
set @i = 0
while @i < 100000
begin
insert T3 values (@i * 5, @i * 11, @i)
set @i = @i + 1
end
Here is a simple example:
select *
from T1 join T2 on T1.a = T2.a
Rows |
Executes |
|
334 |
1 |
|--Hash Match(Inner Join, HASH:([T1].[a])=([T2].[a]), RESIDUAL:([T2].[a]=[T1].[a])) |
1000 |
1 |
|--Table Scan(OBJECT:([T1])) |
10000 |
1 |
|--Table Scan(OBJECT:([T2])) |
Notice that the T2 has ten times as many rows as T1 and indeed the optimizer chooses to use T1 as the build table and T2 as the probe table.
Now consider this three table join:
select *
from (T1 join T2 on T1.a = T2.a)
join T3 on T1.b = T3.a
Rows |
Executes |
|
334 |
1 |
|--Hash Match(Inner Join, HASH:([T1].[b])=([T3].[a]), RESIDUAL:([T1].[b]=[T3].[a])) |
334 |
1 |
|--Hash Match(Inner Join, HASH:([T1].[a])=([T2].[a]), RESIDUAL:([T1].[a]=[T2].[a])) |
1000 |
1 |
| |--Table Scan(OBJECT:([T1])) |
10000 |
1 |
| |--Table Scan(OBJECT:([T2])) |
100000 |
1 |
|--Table Scan(OBJECT:([T3])) |
Note that the optimizer has selected a left deep plan. First, we join the two small tables, T1 and T2. The results of this join yield only 334 rows which we use to build a hash table before joining with the large table T3.
Now observe what happens if we add a predicate to restrict the size of the smaller two tables. (A single where clause suffices; the optimizer can derive “T2.a < 100” from “T1.a < 100” and “T1.a = T2.a”.)
select *
from (T1 join T2 on T1.a = T2.a)
join T3 on T1.b = T3.a
where T1.a < 100
Rows |
Executes |
|
17 |
1 |
|--Hash Match(Inner Join, HASH:([T2].[a])=([T1].[a]), RESIDUAL:([T1].[a]=[T2].[a])) |
34 |
1 |
|--Table Scan(OBJECT:([T2]), WHERE:([T2].[a]<(100))) |
50 |
1 |
|--Hash Match(Inner Join, HASH:([T1].[b])=([T3].[a]), RESIDUAL:([T1].[b]=[T3].[a])) |
50 |
1 |
|--Table Scan(OBJECT:([T1]), WHERE:([T1].[a]<(100))) |
100000 |
1 |
|--Table Scan(OBJECT:([T3])) |
This time the optimizer selected a right deep plan. T1 and T2 are now so small (34 and 50) rows that it is better to build a hash table on these two tables and probe using the large table T3 than it is to build a hash table on an intermediate hash join result.
What next?
Now that I’ve given an overview of how each of the three physical join operators works, in my next post (or two) I plan to summarize the different characteristics of these operators and to give more examples to show how SQL Server makes various tradeoffs when deciding how to join tables.
Comments
- Anonymous
August 16, 2006
CraigFr has a great series of posts in his blog describing the difference between the various logical... - Anonymous
September 12, 2006
Every once in awhile, I get an opportunity to look around for new and interesting things to read.&nbsp;... - Anonymous
November 16, 2006
The comment has been removed - Anonymous
May 02, 2007
Last week I looked at how concurrent updates may cause a scan running at read committed isolation level - Anonymous
June 14, 2007
The comment has been removed - Anonymous
August 07, 2007
Since the beginning of learning SQL Server I'm pretty much confused with JOIN conditions that defines - Anonymous
April 28, 2008
Let's take a look at a simple query: CREATE TABLE T1 (A INT, B CHAR(8)) INSERT T1 VALUES (0, '0') INSERT - Anonymous
October 28, 2008
PingBack from http://grimpidev.wordpress.com/2008/10/28/entender-el-plan-de-ejecucion-en-sql-server-20052008/ - Anonymous
September 21, 2014
The comment has been removed - Anonymous
September 21, 2014
The two residual predicates (and, thus, the two plans) are equivalent as equality is commutative (i.e., the order of the operation does not matter). Simply reversing the order of the predicate in an ON clause (e.g., "ON T1.a = T2.a" vs. "ON T2.a = T1.a") is sufficient to cause this change in the plan due to how the query optimizer generates the residual predicate. HTH, Craig