Représentation matricielle des transformations

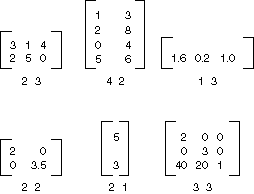
Une matrice m×n est un ensemble de nombres organisés en lignes m et n colonnes. L’illustration suivante montre plusieurs matrices.

Vous pouvez ajouter deux matrices de même taille en ajoutant des éléments individuels. L’illustration suivante montre deux exemples d’ajout de matrice.

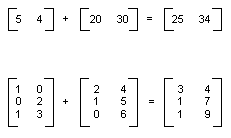
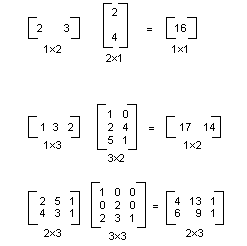
Une matrice m×n peut être multipliée par une matrice n×p, et le résultat est une matrice m×p. Le nombre de colonnes dans la première matrice doit être identique au nombre de lignes de la deuxième matrice. Par exemple, une matrice 4×2 peut être multipliée par une matrice 2×3 pour produire une matrice 4×3.

Les points du plan et des lignes et colonnes d’une matrice peuvent être considérés comme des vecteurs. Par exemple, (2, 5) est un vecteur avec deux composants, et (3, 7, 1) est un vecteur avec trois composants. Le produit par points de deux vecteurs est défini comme suit :

(a, b) • (c, d) = ac + bd

(a, b, c) • (d, e, f) = ad + be + cf

Par exemple, le produit point de (2, 3) et (5, 4) est (2)(5) + (3)(4) = 22. Le produit point de (2, 5, 1) et (4, 3, 1) est (2)(4) + (5)(3) + (1)(1) = 24. Notez que le produit point de deux vecteurs est un nombre, et non un autre vecteur. Notez également que vous pouvez calculer le produit point uniquement si les deux vecteurs ont le même nombre de composants.

Laissez A(i, j) être l’entrée dans la matrice A dans la ligne ith et la colonne jth. Par exemple, A(3, 2) est l’entrée dans la matrice A dans la 3e ligne et la deuxième colonne. Supposons que les matrices A, B et C sont des matrices et AB = C. Les entrées de C sont calculées comme suit :

C(i, j) = (ligne i d’A) • (colonne j de B)

L’illustration suivante montre plusieurs exemples de multiplication de matrices.

Si vous considérez un point dans un plan sous la forme d’une matrice 1×2, vous pouvez transformer ce point en le multipliant par une matrice 2×2. L’illustration suivante montre plusieurs transformations appliquées au point (2, 1).

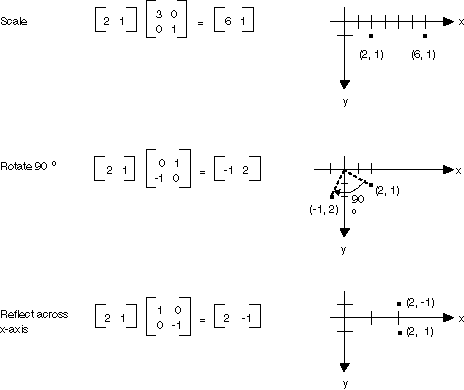
Toutes les transformations présentées dans la figure précédente sont des transformations linéaires. Certaines autres transformations, telles que la traduction, ne sont pas linéaires et ne peuvent pas être exprimées sous forme de multiplication par une matrice 2×2. Supposons que vous voulez commencer par le point (2, 1), le faire pivoter de 90 degrés, le traduire à 3 unités dans le sens x et le traduire 4 unités dans la direction y. Pour ce faire, vous pouvez utiliser une multiplication de matrice suivie d’un ajout de matrice.

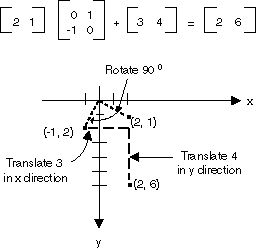
Une transformation linéaire (multiplication par une matrice 2×2) suivie d’une traduction (ajout d’une matrice 1×2) est appelée transformation affine. Une alternative au stockage d’une transformation affine dans une paire de matrices (une pour la partie linéaire et une pour la traduction) consiste à stocker toute la transformation dans une matrice 3×3. Pour effectuer ce travail, un point dans le plan doit être stocké dans une matrice 1×3 avec une coordonnée 3ème factice. La technique habituelle consiste à rendre toutes les coordonnées 3èmes égales à 1. Par exemple, le point (2, 1) est représenté par la matrice [2 1 1]. L’illustration suivante montre une transformation affine (faire pivoter 90 degrés ; traduire 3 unités dans la direction x, 4 unités dans la direction y) exprimée sous forme de multiplication par une matrice de 3×3.

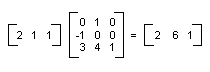
Dans l’exemple précédent, le point (2, 1) est mappé au point (2, 6). Notez que la troisième colonne de la matrice 3×3 contient les nombres 0, 0, 1. Cela sera toujours le cas pour la matrice 3×3 d’une transformation affine. Les nombres importants sont les six nombres des colonnes 1 et 2. La partie supérieure gauche 2×2 de la matrice représente la partie linéaire de la transformation, et les deux premières entrées de la 3e ligne représentent la traduction.

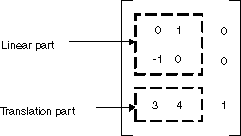
Dans GDI+, vous pouvez stocker une transformation affine dans un Matrix objet. Étant donné que la troisième colonne d’une matrice qui représente une transformation affine est toujours (0, 0, 1), vous spécifiez uniquement les six nombres dans les deux premières colonnes lorsque vous construisez un Matrix objet. L’instruction Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) construit la matrice indiquée dans la figure précédente.

Transformations composites

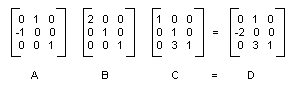
Une transformation composite est une séquence de transformations, l’une suivie de l’autre. Considérez les matrices et les transformations dans la liste suivante :

Matrice	Transformation
Matrice A	Pivoter à 90 degrés
Matrice B	Mettre à l’échelle par un facteur de 2 dans la direction x
Matrice C	Traduire 3 unités dans la direction y

Si nous commençons par le point (2, 1) — représenté par la matrice [2 1 1] — et multipliez par A, puis B, puis C, le point (2, 1) subira les trois transformations dans l’ordre répertorié.

[2 1 1] ABC = [-2 5 1]

Au lieu de stocker les trois parties de la transformation composite dans trois matrices distinctes, vous pouvez multiplier A, B et C ensemble pour obtenir une matrice 3×3 unique qui stocke toute la transformation composite. Supposons ABC = D. Ensuite, un point multiplié par D donne le même résultat qu’un point multiplié par A, puis B, puis C.

[2 1 1] D = [-2 5 1]

L’illustration suivante montre les matrices A, B, C et D.

Le fait que la matrice d’une transformation composite peut être formée en multipliant les matrices de transformation individuelles signifie que toute séquence de transformations affine peut être stockée dans un seul Matrix objet.

Attention

L’ordre d’une transformation composite est important. En général, faire pivoter, puis mettre à l’échelle, puis traduire n’est pas identique à l’échelle, puis faire pivoter, puis traduire. De même, l’ordre de multiplication des matrices est important. En général, ABC n’est pas identique à BAC.

La Matrix classe fournit plusieurs méthodes pour la création d’une transformation composite : Multiply, , RotateRotateAt, Scale, , Shearet Translate. L’exemple suivant crée la matrice d’une transformation composite qui fait d’abord pivoter 30 degrés, puis se met à l’échelle d’un facteur de 2 dans la direction y, puis traduit 5 unités dans la direction x :

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)

L’illustration suivante montre la matrice.

Voir aussi

• Systèmes de coordonnées et transformations
• Utilisation des transformations dans GDI+ managé