Classe System.Drawing.Drawing2D.Matrix

Cet article fournit des remarques supplémentaires à la documentation de référence de cette API.

La Matrix classe encapsule une matrice affine de 3 par 3 qui représente une transformation géométrique.

Dans GDI+, vous pouvez stocker une transformation affine dans un Matrix objet. Étant donné que la troisième colonne d’une matrice qui représente une transformation affine est toujours (0, 0, 1), vous spécifiez uniquement les six nombres dans les deux premières colonnes lorsque vous construisez un objet Matrix. L’instruction Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) construit la matrice indiquée dans la figure suivante.

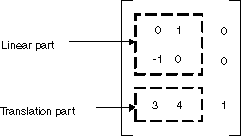
Remarque

Dans .NET 6 et versions ultérieures, le package System.Drawing.Common, qui inclut ce type, n’est pris en charge que sur les systèmes d’exploitation Windows. L’utilisation de ce type dans les applications multiplateformes provoque des avertissements au moment de la compilation et des exceptions d’exécution. Pour plus d’informations, consultez System.Drawing.Common uniquement pris en charge sur Windows.

Transformations composites

Une transformation composite est une séquence de transformations, l’une suivie de l’autre. Considérez les matrices et les transformations dans la liste suivante :

Matrice	Transformation
Matrice A	Pivoter à 90 degrés
Matrice B	Mettre à l’échelle par un facteur de 2 selon l'axe x
Matrice C	Déplacer 3 unités dans la direction y

Si vous commencez par le point (2, 1) - représenté par la matrice [2 1 1] - et multipliez par A, puis B, puis C, le point (2, 1) subira les trois transformations dans l’ordre répertorié.

[2 1 1]ABC = [-2 5 1]

Au lieu de stocker les trois parties de la transformation composite dans trois matrices distinctes, vous pouvez multiplier A, B et C ensemble pour obtenir une matrice 3×3 unique qui stocke toute la transformation composite. Supposons ABC = D. Ensuite, un point multiplié par D donne le même résultat qu’un point multiplié par A, puis B, puis C.

[2 1 1]D = [-2 5 1]

L’illustration suivante montre les matrices A, B, C et D.

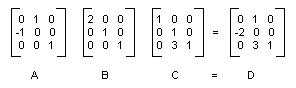
Le fait que la matrice d’une transformation composite peut être formée en multipliant les matrices de transformation individuelles signifie que toute séquence de transformations affine peut être stockée dans un seul objet Matrix.

Avertissement

L’ordre d’une transformation composite est important. En général, effectuer une rotation, puis une mise à l’échelle, puis une translation n’est pas la même chose qu’effectuer une mise à l’échelle, suivie d’une rotation, puis d’une translation. De même, l’ordre de multiplication des matrices est important. En général, ABC n’est pas identique à BAC.

La classe Matrix fournit plusieurs méthodes pour créer une transformation composite : Multiply, Rotate, RotateAt, Scale, Shearet Translate. L’exemple suivant crée la matrice d’une transformation composite qui d'abord effectue une rotation de 30 degrés, puis applique une mise à l'échelle par un facteur de 2 dans la direction y, et enfin se déplace de 5 unités dans la direction x :

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)