Rotations 3D dans SkiaSharp
Utilisez des transformations non affine pour faire pivoter des objets 2D dans l’espace 3D.
Une application courante de transformations non affine consiste à simuler la rotation d’un objet 2D dans un espace 3D :
Ce travail implique l’utilisation de rotations tridimensionnelles, puis la dérivation d’une transformation non affine SKMatrix qui effectue ces rotations 3D.
Il est difficile de développer cette SKMatrix transformation qui fonctionne uniquement dans deux dimensions. Le travail devient beaucoup plus facile lorsque cette matrice 3 par 3 est dérivée d’une matrice 4 par 4 utilisée dans les graphiques 3D. SkiaSharp inclut la SKMatrix44 classe à cet effet, mais certains arrière-plans dans les graphiques 3D sont nécessaires pour comprendre les rotations 3D et la matrice de transformation de 4 à 4.
Un système de coordonnées tridimensionnel ajoute un troisième axe appelé Z. Conceptuellement, l’axe Z est aux angles droit de l’écran. Les points de coordonnées dans l’espace 3D sont indiqués avec trois nombres : (x, y, z). Dans le système de coordonnées 3D utilisé dans cet article, l’augmentation des valeurs de X est à droite et l’augmentation des valeurs de Y descend, comme dans deux dimensions. L’augmentation des valeurs Z positives sort de l’écran. L’origine est le coin supérieur gauche, comme dans les graphiques 2D. Vous pouvez considérer l’écran comme un plan XY avec l’axe Z aux angles droit de ce plan.
Il s’agit d’un système de coordonnées gauche. Si vous pointez le forefinger pour votre main gauche dans la direction des coordonnées X positives (vers la droite) et votre doigt central dans la direction d’augmentation des coordonnées Y (bas), puis vos points de pouce dans la direction de l’augmentation des coordonnées Z ( s’étendant à partir de l’écran).
Dans les graphiques 3D, les transformations sont basées sur une matrice de 4 à 4. Voici la matrice d’identité 4 par 4 :
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Pour utiliser une matrice de 4 par 4, il est pratique d’identifier les cellules avec leurs numéros de ligne et de colonne :
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Toutefois, la classe SkiaSharp Matrix44 est un peu différente. La seule façon de définir ou d’obtenir des valeurs SKMatrix44 de cellule individuelles consiste à utiliser l’indexeur Item . Les index de ligne et de colonne sont basés sur zéro plutôt que sur une base unique, et les lignes et colonnes sont permutées. La cellule M14 du diagramme ci-dessus est accessible à l’aide de l’indexeur [3, 0] dans un SKMatrix44 objet.
Dans un système graphique 3D, un point 3D (x, y, z) est converti en matrice 1 par 4 pour la multiplication par la matrice de transformation 4 par 4 :
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Analogues aux transformations 2D qui ont lieu en trois dimensions, les transformations 3D sont supposées avoir lieu en quatre dimensions. La quatrième dimension est appelée W, et l’espace 3D est supposé exister dans l’espace 4D où les coordonnées W sont égales à 1. Les formules de transformation sont les suivantes :
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Il est évident à partir des formules de transformation que les cellules M11, M33M22sont des facteurs de mise à l’échelle dans les directions X, Y et Z, et M43M41M42sont des facteurs de traduction dans les directions X, Y et Z.
Pour convertir ces coordonnées en espace 3D où W est égal à 1, les coordonnées x', y et z' sont toutes divisées par w' :
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Cette division par w' fournit une perspective dans l’espace 3D. Si w' est égal à 1, aucune perspective ne se produit.
Les rotations dans l’espace 3D peuvent être assez complexes, mais les rotations les plus simples sont celles autour des axes X, Y et Z. Une rotation d’angle α autour de l’axe X est cette matrice :
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Les valeurs de X restent identiques lorsqu’elles sont soumises à cette transformation. La rotation autour de l’axe Y laisse les valeurs de Y inchangées :
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
La rotation autour de l’axe Z est la même que dans les graphiques 2D :
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
La direction de la rotation est implicite par la remise du système de coordonnées. Il s’agit d’un système gaucher, donc si vous pointez le pouce de la main gauche vers des valeurs croissantes pour un axe particulier — à droite pour la rotation autour de l’axe X, vers le bas pour la rotation autour de l’axe Y, et vers vous pour la rotation autour de l’axe Z , la courbe de vos autres doigts indique la direction de rotation pour les angles positifs.
SKMatrix44 a généralisé des méthodes statiques CreateRotation et CreateRotationDegrees qui vous permettent de spécifier l’axe autour duquel la rotation se produit :
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Pour la rotation autour de l’axe X, définissez les trois premiers arguments sur 1, 0, 0. Pour la rotation autour de l’axe Y, définissez-les sur 0, 1, 0 et pour la rotation autour de l’axe Z, définissez-les sur 0, 0, 1.
La quatrième colonne du 4 par 4 est destinée à la perspective. Il SKMatrix44 n’existe aucune méthode pour créer des transformations de perspective, mais vous pouvez en créer une vous-même à l’aide du code suivant :
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
La raison du nom depth de l’argument sera évidente sous peu. Ce code crée la matrice :
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Les formules de transformation entraînent le calcul suivant de w' :
w' = –z / depth + 1
Cela permet de réduire les coordonnées X et Y lorsque les valeurs de Z sont inférieures à zéro (conceptuellement derrière le plan XY) et pour augmenter les coordonnées X et Y pour les valeurs positives de Z. Lorsque la coordonnée Z est égale depth, alors w' est zéro, et les coordonnées deviennent infinies. Les systèmes graphiques à trois dimensions sont construits autour d’une métaphore de caméra, et la depth valeur ici représente la distance de la caméra de l’origine du système de coordonnées. Si un objet graphique a une coordonnée Z qui est depth des unités de l’origine, il touche conceptuellement l’objectif de la caméra et devient infiniment grand.
N’oubliez pas que vous utiliserez probablement cette perspectiveMatrix valeur en combinaison avec les matrices de rotation. Si un objet graphique pivoté a des coordonnées X ou Y supérieures depthà , la rotation de cet objet dans l’espace 3D est susceptible d’impliquer des coordonnées Z supérieures à depth. Cela doit être évité ! Lorsque vous créez perspectiveMatrixdepth une valeur suffisamment grande pour toutes les coordonnées de l’objet graphique, quelle que soit la façon dont elle est pivotée. Cela garantit qu’il n’y a jamais de division par zéro.
La combinaison de rotations 3D et de perspective nécessite de multiplier les matrices 4 par 4 ensemble. À cet effet, SKMatrix44 définit les méthodes de concaténation. Si A et B sont SKMatrix44 des objets, le code suivant définit A égal à A × B :
A.PostConcat(B);
Lorsqu’une matrice de transformation 4 par 4 est utilisée dans un système graphique 2D, elle est appliquée aux objets 2D. Ces objets sont plats et sont supposés avoir des coordonnées Z de zéro. La multiplication des transformations est un peu plus simple que la transformation indiquée précédemment :
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Cette valeur de 0 pour z génère des formules de transformation qui n’impliquent aucune cellule dans la troisième ligne de la matrice :
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
De plus, la coordonnée z n’est pas pertinente ici aussi. Lorsqu’un objet 3D est affiché dans un système graphique 2D, il est réduit à un objet à deux dimensions en ignorant les valeurs de coordonnées Z. Les formules de transformation sont vraiment les deux suivantes :
x" = x' / w'
y" = y' / w'
Cela signifie que la troisième ligne et la troisième colonne de la matrice 4 par 4 peuvent être ignorées.
Mais si c’est le cas, pourquoi la matrice de 4 par 4 est-elle même nécessaire en premier lieu ?
Bien que la troisième ligne et la troisième colonne des 4 par 4 ne soient pas pertinentes pour les transformations à deux dimensions, la troisième ligne et la troisième colonne jouent un rôle avant cela lorsque différentes SKMatrix44 valeurs sont multipliées ensemble. Par exemple, supposons que vous multipliez la rotation autour de l’axe Y avec la transformation de perspective :
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
Dans le produit, la cellule M14 contient maintenant une valeur de perspective. Si vous souhaitez appliquer cette matrice à des objets 2D, la troisième ligne et la colonne sont supprimées pour la convertir en matrice 3 par 3 :
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Il peut maintenant être utilisé pour transformer un point 2D :
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Les formules de transformation sont les suivantes :
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Divisez maintenant tout par z' :
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Lorsque les objets 2D sont pivotés avec un angle positif autour de l’axe Y, les valeurs X positives sont répliquées vers l’arrière-plan tandis que les valeurs X négatives sont au premier plan. Les valeurs X semblent se rapprocher de l’axe Y (qui est régie par la valeur cosinus), car les coordonnées les plus éloignées de l’axe Y deviennent plus petites ou plus grandes quand elles se déplacent plus loin de la visionneuse ou plus près de la visionneuse.
Lors de l’utilisation SKMatrix44, effectuez toutes les opérations de rotation et de perspective 3D en multipliant différentes SKMatrix44 valeurs. Vous pouvez ensuite extraire une matrice 3 par 3 à 3 à partir de la matrice 4 par 4 à 4 à l’aide de la Matrix propriété de la SKMatrix44 classe. Cette propriété retourne une valeur familière SKMatrix .
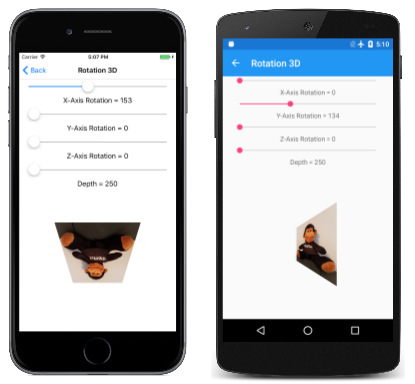
La page Rotation 3D vous permet d’expérimenter la rotation 3D. Le fichier Rotation3DPage.xaml instancie quatre curseurs pour définir la rotation autour des axes X, Y et Z, et pour définir une valeur de profondeur :
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Notez que le depthSlider fichier est initialisé avec une Minimum valeur de 250. Cela implique que l’objet 2D pivoté ici comporte des coordonnées X et Y limitées à un cercle défini par un rayon de 250 pixels autour de l’origine. Toute rotation de cet objet dans l’espace 3D entraîne toujours des valeurs de coordonnées inférieures à 250.
Le Rotation3DPage.cs fichier code-behind se charge dans une bitmap de 300 pixels carrés :
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Si la transformation 3D est centrée sur cette bitmap, les coordonnées X et Y sont comprises entre –150 et 150, tandis que les angles sont de 212 pixels à partir du centre, donc tout se trouve dans le rayon de 250 pixels.
Le PaintSurface gestionnaire crée des SKMatrix44 objets basés sur les curseurs et les multiplie à l’aide PostConcatde . La SKMatrix valeur extraite de l’objet final SKMatrix44 est entourée de transformations de traduction pour centrer la rotation au centre de l’écran :
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Lorsque vous expérimentez le quatrième curseur, vous remarquerez que les différents paramètres de profondeur ne déplacent pas l’objet plus loin de la visionneuse, mais modifiez plutôt l’étendue de l’effet de perspective :
La rotation animée 3D utilise SKMatrix44 également pour animer une chaîne de texte dans un espace 3D. L’objet textPaint défini en tant que champ est utilisé dans le constructeur pour déterminer les limites du texte :
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Le OnAppearing remplacement définit trois Xamarin.FormsAnimation objets pour animer les champs et yRotationDegreeszRotationDegrees les xRotationDegreeschamps à différents taux. Notez que les périodes de ces animations sont définies sur des nombres premiers (5 secondes, 7 secondes et 11 secondes) de sorte que la combinaison globale se répète uniquement toutes les 385 secondes, ou plus de 10 minutes :
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Comme dans le programme précédent, le PaintCanvas gestionnaire crée SKMatrix44 des valeurs pour la rotation et la perspective, et les multiplie ensemble :
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Cette rotation 3D est entourée de plusieurs transformations 2D pour déplacer le centre de rotation vers le centre de l’écran, et pour mettre à l’échelle la taille de la chaîne de texte afin qu’elle soit la même largeur que l’écran :