Équations PRT (Direct3D 9)

Pour bien comprendre un nuanceur qui implémente PRT, il est utile de dériver la formule utilisée par le nuanceur pour calculer le rayonnement de sortie.

Pour commencer, l’équation suivante est l’équation générale pour calculer l’éclat de sortie résultant de l’éclairage direct sur un objet diffus avec un éclairage distant arbitraire.

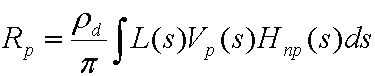
où :

Paramètre	Description
Rp	L’éclat de sortie au sommet p. Évalué à chaque sommet du maillage.
pd	Albédo de la surface.
pi	Constante utilisée comme facteur de normalisation de la conservation de l’énergie.
L(s)	L’environnement d’éclairage (rayonnement source).
Vp₍s₎	Fonction de visibilité binaire pour point p. Il est 1 si le point peut voir la lumière, 0 si ce n’est pas le cas.
Hnp₍s₎	Terme cosinus de la loi de Lambert. Égal à max((Np· s), 0) où Np est la normale de surface au point p.
s	Variable qui s’intègre sur la sphère.

 

À l’aide de fonctions de base sphériques, telles que les harmoniques sphériques, l’équation suivante se rapproche de l’environnement d’éclairage.

où :

Paramètre	Description
L(s)	L’environnement d’éclairage (rayonnement source).
i	Entier qui additionne le nombre de fonctions de base.
O	Ordre des harmoniques sphériques.
li i	Coefficient.
Yi(s)	Certaines fonctions de base sur la sphère.

 

La collection de ces coefficients, L', fournit l’approximation optimale pour la fonction L(s) avec les fonctions de base Y(s). La substitution et la distribution donnent l’équation suivante.

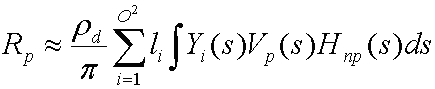
L’intégrale de Y_i(s)Vp₍s₎Hnp₍s₎ est un coefficient de transfert t_pi que le simulateur précompute pour chaque sommet du maillage. La substitution de cette valeur donne l’équation suivante.

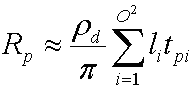
Le fait de passer à la notation vectorielle génère l’équation non compressée suivante pour calculer le rayonnement de sortie pour chaque canal.

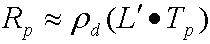
où :

Paramètre	Description
Rp	L’éclat de sortie au sommet p.
pd	Albédo de la surface.
L'	Vecteur de li, et est la projection de l’éclat source dans les fonctions de base harmonique sphérique. Il s’agit d’un vecteur order² de coefficients harmoniques sphériques.
Tp	Vecteur de transfert order² pour le vertex p. Le simulateur divise les coefficients de transfert par p.

 

Ces deux vecteurs sont un vecteur order² de coefficients harmoniques sphériques, notez donc qu’il s’agit simplement d’un produit à points. Selon l’ordre, le point peut être coûteux et la compression peut être utilisée. Un algorithme appelé CPCA (Clustered Principal Component Analysis) compresse efficacement les données. Cela permet d’utiliser une approximation harmonique sphérique d’ordre supérieur qui se traduit par des ombres plus nettes.

CPCA fournit l’équation suivante pour approximativement le vecteur de transfert.

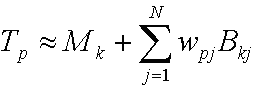
où :

Paramètre	Description
Tp	Vecteur de transfert pour le vertex p.
Mk	Moyenne du cluster k.
j	Entier qui additionne le nombre de vecteurs PCA.
N	Nombre de vecteurs PCA.
wpj	Poids jième PCA pour le point p.
Bkj	Vecteur de base PCA jth pour le cluster k.

 

Un cluster est simplement un certain nombre de sommets qui partagent le même vecteur moyen. Vous trouverez ci-dessous la moyenne du cluster, les pondérations PCA, les vecteurs de base pcA et les ID de cluster pour les sommets.

La substitution de ces deux équations donne :

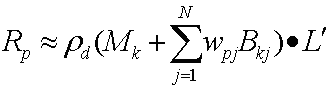
Ensuite, la distribution du produit point donne l’équation suivante.

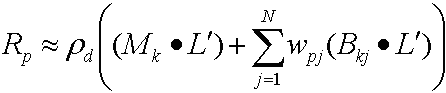
Parce que les deux (Mk· L') et (B_kj· L') sont constantes par vertex, l’exemple calcule ces valeurs avec le processeur et les passe en tant que constantes dans le nuanceur de vertex ; étant donné que w_pj change pour chaque vertex, l’exemple stocke ces données par vertex dans la mémoire tampon de vertex.

Rubriques connexes

Transfert de rayonnement précalculé