Rotation

De nombreuses applications CAO fournissent des fonctionnalités qui font pivoter les objets dessinés dans la zone cliente. Les applications qui incluent des fonctionnalités de rotation utilisent la fonction SetWorldTransform pour définir l’espace universel approprié sur la transformation de l’espace de page. Cette fonction reçoit un pointeur vers une structureXFORMcontenant les valeurs appropriées. Les membres eM11, eM12, eM21 et eM22 de XFORM spécifient respectivement le cosinus, le sinus, le sinus négatif et le cosinus de l’angle de rotation.

Lorsque rotation se produit, les points qui constituent un objet sont pivotés par rapport à l’origine de l’espace de coordonnées. L’illustration suivante montre un rectangle de 20 à 20 unités pivoté de 30 degrés lors de la copie de l’espace de coordonnées du monde à l’espace de coordonnées de page.

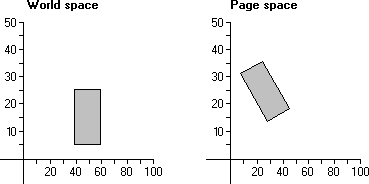
Dans l’illustration précédente, chaque point du rectangle a été pivoté de 30 degrés par rapport à l’origine de l’espace de coordonnées.

L’algorithme suivant calcule la nouvelle coordonnée x (x ') pour un point (x,y) qui est pivoté par angle A par rapport à l’origine de l’espace de coordonnées.

x' = (x * cos A) - (y * sin A) 

L’algorithme suivant calcule la coordonnée y (y') d’un point (x,y) qui est pivoté par l’angle A par rapport à l’origine.

y' = (x * sin A) + (y * cos A) 

Les deux transformations de rotation peuvent être combinées dans une matrice de 2 à 2, comme suit.

|x' y'| == |x y| * | cos A   sin A| 
                   |-sin A   cos A| 

La matrice 2 par 2 qui a produit la rotation contient les valeurs suivantes.

| .8660    .5000| 
|-.5000    .8660| 

Dérivation de l’algorithme de rotation

Les algorithmes de rotation sont basés sur le théorème d’addition de trigonométrie indiquant que la fonction trigonométrique d’une somme de deux angles (A1 et A2) peut être exprimée en termes de fonctions trigonométriques des deux angles.

sin(A1 + A2) = (sin A1 * cos A2) + (cos A1 * sin A2) 
cos(A1 + A2) = (cos A1 * cos A2) - (sin A1 * sin A2) 

L’illustration suivante montre un point p pivoté dans le sens inverse vers une nouvelle position p'. En outre, il montre deux triangles formés par une ligne dessinée de l’origine de l’espace de coordonnées à chaque point et une ligne dessinée à partir de chaque point à travers l’axe x.

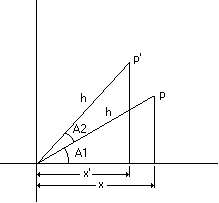
À l’aide de trigonométrie, la coordonnée x du point p peut être obtenue en multipliant la longueur de l’hypotenuse h par le cosinus d’A1.

x = h * cos A1 

La coordonnée y du point p peut être obtenue en multipliant la longueur de l’hypotenuse h par le sinus de A1.

y = h * sin A1 

De même, la coordonnée x du point p' peut être obtenue en multipliant la longueur de l’hypotenuse h par le cosinus de (A1 +A2).

x' = h * cos (A1 + A2) 

Enfin, la coordonnée y du point p' peut être obtenue en multipliant la longueur de l’hypotenuse h par le sinus de (A1 +A2).

y' = h * sin (A1 + A2) 

À l’aide du théorème d’ajout, les algorithmes précédents deviennent les suivants :

x' = (h * cos A1 * cos A2) - (h * sin A1 * sin A2) 
y' = (h * cos A1 * sin A2) + (h * sin A1 * cos A2) 

Les algorithmes de rotation d’un point donné pivotés par angle A2 peuvent être obtenus en remplaçant x pour chaque occurrence de (h * cos A1) et en remplaçant y pour chaque occurrence de (h * sin A1).

x' = (x * cos A2) - (y * sin A2) 
y' = (x * sin A2) + (y * cos A2)