Remarque
L’accès à cette page nécessite une autorisation. Vous pouvez essayer de vous connecter ou de modifier des répertoires.
L’accès à cette page nécessite une autorisation. Vous pouvez essayer de modifier des répertoires.
Cette rubrique fournit une vue d’ensemble mathématique des transformations de matrice pour les graphiques 2D. Toutefois, vous n’avez pas besoin de connaître les mathématiques de matrice pour utiliser des transformations dans Direct2D. Lisez cette rubrique si vous êtes intéressé par les mathématiques ; sinon, n’hésitez pas à ignorer cette rubrique.
- Présentation des matrices
- transformations affine
- transformation de traduction
- transformation de mise à l’échelle
- rotation autour de l’origine
- rotation autour d’un point arbitraire
- de transformation d’asymétrie
- représentant des transformations dans direct2D
- suivante
Introduction aux matrices
Une matrice est un tableau rectangulaire de nombres réels. L’ordre de la matrice correspond au nombre de lignes et de colonnes. Par exemple, si la matrice comporte 3 lignes et 2 colonnes, l’ordre est de 3 × 2. Les matrices sont généralement affichées avec les éléments de matrice placés entre crochets :
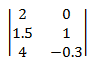
Notation : une matrice est désignée par une lettre majuscule. Les éléments sont désignés par des lettres minuscules. Les indices indiquent le numéro de ligne et de colonne d’un élément. Par exemple, uneij est l’élément situé à la i’ième ligne et à la j’ième colonne de la matrice A.
Le diagramme suivant montre une matrice i × j, avec les éléments individuels dans chaque cellule de la matrice.

Opérations de matrice
Cette section décrit les opérations de base définies sur les matrices.
addition. La somme A + B de deux matrices est obtenue en ajoutant les éléments correspondants de A et B :
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
multiplication scalaire. Cette opération multiplie une matrice par un nombre réel. Étant donné un nombre réel k, le produit scalaire kA est obtenu en multipliant chaque élément de A par k.
- kA = k\[ a*ij* \] = \[ k × a*ij* \]
la multiplication de matrices. Étant donné deux matrices A et B avec ordre (m × n) et (n × p), le produit C = A × B est une matrice avec ordre (m × p), définie comme suit :
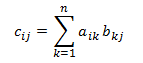
ou, en équivalent :
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*
Autrement dit, pour calculer chaque élément cij, procédez comme suit :
- Prenez la i’ième ligne de A et la j’ième colonne de B.
- Multipliez chaque paire d’éléments dans la ligne et la colonne : la première entrée de ligne par la première entrée de colonne, la deuxième entrée de ligne par la deuxième entrée de colonne, etc.
- Additionnez le résultat.
Voici un exemple de multiplication d’une matrice (2 × 2) par une matrice (2 × 3).
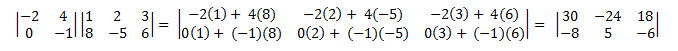
La multiplication de matrices n’est pas commutative. Autrement dit, A × B ≠ B × A. En outre, à partir de la définition, il suit que toutes les paires de matrices peuvent être multipliées. Le nombre de colonnes de la matrice de gauche doit être égal au nombre de lignes de la matrice de droite. Sinon, l’opérateur × n’est pas défini.
Identifier la matrice. Une matrice d’identité, désignée I, est une matrice carrée définie comme suit :
- I*ij* = 1 si *i* = *j*, ou 0 sinon.
En d’autres termes, une matrice d’identité contient 1 pour chaque élément où le numéro de ligne est égal au nombre de colonnes et zéro pour tous les autres éléments. Par exemple, voici la matrice d’identité 3 × 3.
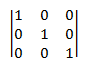
Les égalités suivantes tiennent pour n’importe quelle matrice M.
- M x I = M I x M = M
Transformations affine
Une transformation affine est une opération mathématique qui mappe un espace de coordonnées à un autre. En d’autres termes, il mappe un ensemble de points à un autre ensemble de points. Les transformations affine ont des fonctionnalités qui les rendent utiles dans les graphiques informatiques.
- Les transformations affine préservent colline. Si trois points ou plus tombent sur une ligne, ils forment toujours une ligne après la transformation. Les lignes droites restent droites.
- La composition de deux transformations affine est une transformation affine.
Les transformations affine pour l’espace 2D ont la forme suivante.
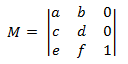
Si vous appliquez la définition de la multiplication de matrice donnée précédemment, vous pouvez montrer que le produit de deux transformations affine est une autre transformation affine. Pour transformer un point 2D à l’aide d’une transformation affine, le point est représenté sous la forme d’une matrice 1 × 3.
- P = \| x y 1 \|
Les deux premiers éléments contiennent les coordonnées x et y du point. Le 1 est placé dans le troisième élément pour que les mathématiques fonctionnent correctement. Pour appliquer la transformation, multipliez les deux matrices comme suit.
- P' = P × M
Cela s’étend à ce qui suit.
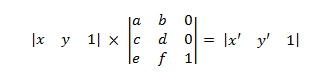
où
- x' = ax + cy + e y' = bx + dy + f
Pour obtenir le point transformé, prenez les deux premiers éléments de la matrice P'.
- p = (x', y') = (ax + cy + e, bx + dy + f)
Note
Une matrice × n est appelée vecteur de ligne. Direct2D et Direct3D utilisent tous deux des vecteurs de ligne pour représenter des points dans l’espace 2D ou 3D. Vous pouvez obtenir un résultat équivalent à l’aide d’un vecteur de colonne (n × 1) et de transposer la matrice de transformation. La plupart des textes graphiques utilisent la forme de vecteur de colonne. Cette rubrique présente la forme de vecteur de ligne pour la cohérence avec Direct2D et Direct3D.
Les sections suivantes dérivent les transformations de base.
Transformation de traduction
La matrice de transformation de traduction comporte la forme suivante.
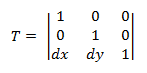
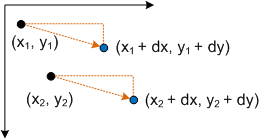
Le branchement d’un point P dans cette équation génère :
- P' = (*x* + *dx*, *y* + *dy*)
qui correspond au point (x, y) traduit par dx dans l’axe X et dans l’axe Y.
Transformation de mise à l’échelle
La matrice de transformation de mise à l’échelle comporte le formulaire suivant.
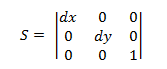
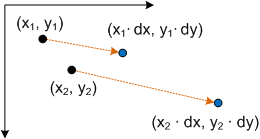
Le branchement d’un point P dans cette équation génère :
- P' = (*x* × *dx*, *y* • *dy*)
qui correspond au point (x,y) mis à l’échelle par dx et dy .
Rotation autour de l’origine
La matrice pour faire pivoter un point autour de l’origine a la forme suivante.
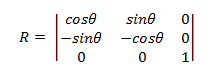
Le point transformé est :
- P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)
Preuve. Pour montrer que P' représente une rotation, tenez compte du diagramme suivant.
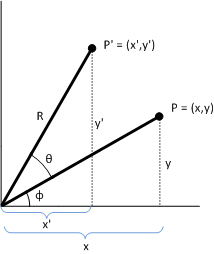
Donné:
-
P = (x,y)
-
Point d’origine à transformer.
-
Φ
-
Angle formé par la ligne (0,0) à P.
-
Θ
-
Angle par lequel faire pivoter (x,y) à propos de l’origine.
-
P' = (x',y')
-
Point transformé.
-
R
-
Longueur de la ligne (0,0) à P. Également le rayon du cercle de rotation.
Note
Ce diagramme utilise le système de coordonnées standard utilisé dans la géométrie, où l’axe y positif pointe vers le haut. Direct2D utilise le système de coordonnées Windows, où l’axe y positif pointe vers le bas.
L’angle entre l’axe x et la ligne (0,0) à P' est Φ + Θ. Les identités suivantes contiennent :
- x = R cosΦ y = R sinΦ x' = R cos(Φ + Θ) y' = R sin(Φ+ Θ)
Maintenant, résolvez pour x' et y' en termes de Θ. Par les formules d’addition trigonométrique :
- x' = R(cosΦcosΘ – sinΦsinΘ) = RcosΦcosΘ – RsinΦsinΘ y' = R(sinΦcosΘ + cosΦsinΘ) = RsinΦcosΘ + RcosΦsinΘ
En remplaçant, nous obtenons :
- x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ
qui correspond au point transformé P' illustré précédemment.
Rotation autour d’un point arbitraire
Pour faire pivoter autour d’un point (x,y) autre que l’origine, la matrice suivante est utilisée.
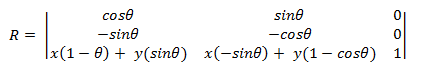
Vous pouvez dériver cette matrice en prenant le point (x,y) comme origine.
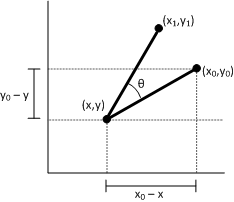
Laissez (x1, y1) être le point qui résulte de la rotation du point (x0, y0) autour du point (x,y). Nous pouvons dériver x1 comme suit.
- x1 = (x0 – x)cosΘ – (y0 – y)sinΘ + x x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]
Maintenant, connectez cette équation à la matrice de transformation, à l’aide de la formule x1 = ax0 + cy0 + e à partir d’une version antérieure. Utilisez la même procédure pour dériver y1.
Transformation d’asymétrie
La transformation d’asymétrie est définie par quatre paramètres :
- Θ : la quantité d’asymétrie le long de l’axe x, mesurée sous la forme d’un angle de l’axe y.
- Ґ : La quantité à faire l’objet d’une asymétrie le long de l’axe y, mesurée sous la forme d’un angle de l’axe x.
- (px, py) : coordonnées x et y du point sur lequel l’asymétrie est effectuée.
La transformation d’asymétrie utilise la matrice suivante.
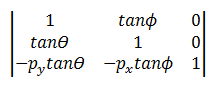
Le point transformé est :
- P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΦ) – *py*tanΦ
ou équivalent :
- P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΦ)
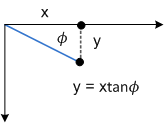
Pour voir comment cette transformation fonctionne, envisagez chaque composant individuellement. Le paramètre Θ déplace chaque point dans la direction x d’une quantité égale à tanΘ. Le diagramme suivant montre la relation entre Θ et l’asymétrie de l’axe x.
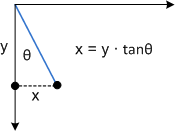
Voici la même asymétrie appliquée à un rectangle :
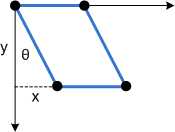
Le paramètre Φ a le même effet, mais le long de l’axe y :
Le diagramme suivant montre l’asymétrie de l’axe y appliquée à un rectangle.
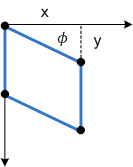
Enfin, les paramètres px et py décaler le point central pour l’asymétrie le long des axes x et y.
Représentation de transformations dans Direct2D
Toutes les transformations Direct2D sont des transformations affine. Direct2D ne prend pas en charge les transformations non affine. Les transformations sont représentées par la structure D2D1_MATRIX_3X2_F. Cette structure définit une matrice 3 × 2. Étant donné que la troisième colonne d’une transformation affine est toujours la même ([0, 0, 1]), et parce que Direct2D ne prend pas en charge les transformations non affine, il n’est pas nécessaire de spécifier l’ensemble de la matrice 3 × 3. En interne, Direct2D utilise 3 matrices × 3 pour calculer les transformations.
Les membres de la D2D1_MATRIX_3X2_F sont nommés en fonction de leur position d’index : le membre _11 est l’élément (1,1), le membre _12 est l’élément (1,2), etc. Bien que vous puissiez initialiser directement les membres de la structure, il est recommandé d’utiliser la classe D2D1 ::Matrix3x2F. Cette classe hérite D2D1_MATRIX_3X2_F et fournit des méthodes d’assistance pour créer l’une des transformations affine de base. La classe définit également opérateur*() pour la composition de deux transformations ou plus, comme décrit dans Application de transformations dans Direct2D.
Prochain