Valutare i modelli di classificazione
L'accuratezza di training di un modello di classificazione è molto meno importante rispetto al grado di funzionamento del modello con dati nuovi e non visti in precedenza. Il training dei modelli, in fin dei conti, viene eseguito perché possano essere usati con dati nuovi presenti nel mondo reale. Dopo aver eseguito il training di un modello di classificazione, se ne valuteranno le prestazioni con un set di nuovi dati non visti in precedenza.
Nelle unità precedenti è stato creato un modello che consentiva di stimare se un paziente avesse il diabete o meno in base al livello di glicemia. Se viene applicato ora a un insieme di dati che non fa parte del set di training, si ottengono le stime seguenti.
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |
Tenere presente che x si riferisce al livello di glicemia di un paziente, y indica se è effettivamente diabetico e ŷ fa riferimento alla stima del modello per stabilire se è diabetico o meno.
Il mero calcolo del numero di stime corrette è talvolta fuorviante o troppo semplicistico per capire i tipi di errori che verranno generati nel mondo reale. Per acquisire informazioni più dettagliate, è possibile tabulare i risultati in una struttura denominata matrice di confusione, come illustrato di seguito:
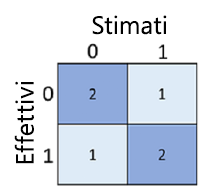
La matrice di confusione mostra il numero totale di casi in cui:
- Il modello ha previsto 0 e l'etichetta effettiva è 0 (veri negativi, in alto a sinistra)
- Il modello ha previsto 1 e l'etichetta effettiva è 1 (veri positivi, in basso a destra)
- Il modello ha previsto 0 e l'etichetta effettiva è 1 (falsi negativi, in basso a sinistra)
- Il modello ha previsto 1 e l'etichetta effettiva è 0 (veri positivi, in alto a destra)
Alle celle in una matrice di confusione vengono spesso applicate gradazioni di colore in modo che i valori più alti abbiano una gradazione più scura. In questo modo è più semplice visualizzare una forte tendenza diagonale da in alto a sinistra a in basso a destra, evidenziando le celle in cui il valore previsto e il valore effettivo sono uguali.
Da questi valori di base è possibile calcolare un intervallo di altre metriche che consentono di valutare le prestazioni del modello. Ad esempio:
- Accuratezza: (TP+TN)/(TP+TN+FP+FN) - di tutte le previsioni, quante erano corrette?
- Richiamo: TP/(TP+FN) - di tutti i casi che sono positivi, quanti ne ha identificati il modello?
- Precisione: TP/(TP+FP) - di tutti i casi che il modello prevedeva essere positivi, quanti sono effettivamente positivi?