Rappresentazione tramite matrici delle trasformazioni

Una matrice m×n è un set di numeri disposti in m righe e n colonne. La figura seguente mostra diverse matrici.

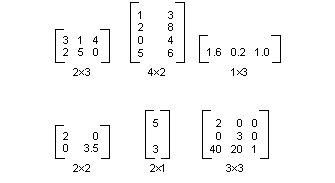
È possibile aggiungere due matrici della stessa dimensione aggiungendo singoli elementi. La figura seguente mostra due esempi di addizione della matrice.

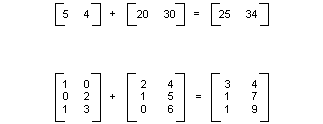
Una matrice m×n può essere moltiplicata per una matrice n×p e il risultato è una matrice m×p . Il numero di colonne nella prima matrice deve essere uguale al numero di righe nella seconda matrice. Ad esempio, una matrice 4 ×2 può essere moltiplicata per una matrice di 2 ×3 per produrre una matrice di 4 ×3.

I punti nel piano e nelle righe e nelle colonne di una matrice possono essere considerati come vettori. Ad esempio, (2, 5) è un vettore con due componenti e (3, 7, 1) è un vettore con tre componenti. Il prodotto punto di due vettori è definito come segue:

(a, b) • (c, d) = ac + bd

(a, b, c) • (d, e, f) = ad + be + cf

Ad esempio, il prodotto punto di (2, 3) e (5, 4) è (2)(5) + (3)(4) = 22. Il prodotto punto di (2, 5, 1) e (4, 3, 1) è (2)(4) + (5)(3) + (1)(1) = 24. Si noti che il prodotto punto di due vettori è un numero, non un altro vettore. Si noti anche che è possibile calcolare il prodotto punto solo se i due vettori hanno lo stesso numero di componenti.

Let A(i, j) be the entry in matrix A in the ith row and the jth column. Ad esempio, A(3, 2) è la voce nella matrice A nella riga 3rd e nellaseconda colonna. Si supponga che A, B e C siano matrici e AB = C. Le voci di C vengono calcolate come segue:

C(i, j) = (riga i di A) • (colonna j di B)

La figura seguente mostra diversi esempi di moltiplicazione della matrice.

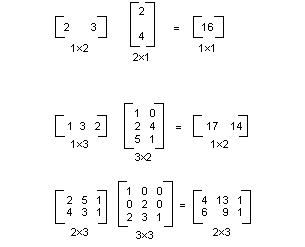
Se si pensa a un punto nel piano come una matrice 1 × 2, è possibile trasformare tale punto moltiplicandolo per una matrice 2 × 2. La figura seguente mostra diverse trasformazioni applicate al punto (2, 1).

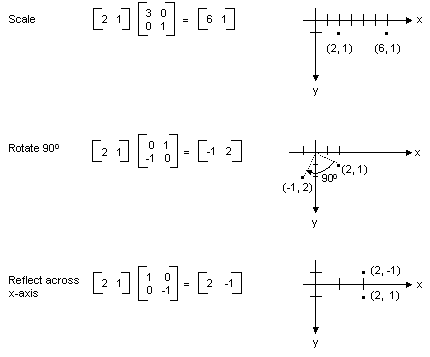
Tutte le trasformazioni illustrate nella figura precedente sono trasformazioni lineari. Alcune altre trasformazioni, ad esempio la traduzione, non sono lineari e non possono essere espresse come moltiplicazione per una matrice 2 × 2. Si supponga di voler iniziare con il punto (2, 1), ruotarlo di 90 gradi, convertirlo 3 unità nella direzione x e convertirlo 4 unità nella direzione y. A tale scopo, è possibile eseguire una moltiplicazione di matrice seguita da un'aggiunta di matrice.

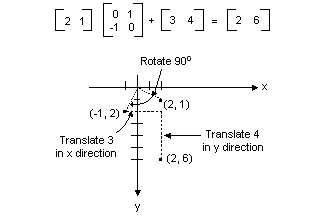
Una trasformazione lineare (moltiplicazione per una matrice 2 × 2) seguita da una traslazione (aggiunta di una matrice 1 × 2) è detta trasformazione affine. Un'alternativa all'archiviazione di una trasformazione affine in una coppia di matrici (una per la parte lineare e una per la traslazione) consiste nell'archiviare l'intera trasformazione in una matrice di 3 × 3. Per eseguire questa operazione, un punto nel piano deve essere archiviato in una matrice di 1 × 3 con una coordinata fittizia 3. La tecnica consueta consiste nel creare tutte le tre coordinate uguali a 1. Ad esempio, il punto (2, 1) è rappresentato dalla matrice [2 1 1]. La figura seguente mostra una trasformazione affine (ruotare 90 gradi; tradurre 3 unità nella direzione x, 4 unità nella direzione y) espresse come moltiplicazione per un singolo 3 × 3 matrice.

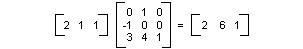
Nell'esempio precedente viene eseguito il mapping del punto (2, 1) al punto (2, 6). Si noti che la terza colonna della matrice 3 × 3 contiene i numeri 0, 0, 1. Questo sarà sempre il caso per la matrice 3 × 3 di una trasformazione affine. I numeri importanti sono i sei numeri nelle colonne 1 e 2. La parte superiore sinistra 2 × 2 della matrice rappresenta la parte lineare della trasformazione e le prime due voci nella terza riga rappresentano la traslazione.

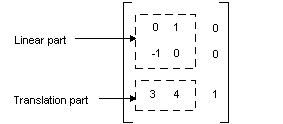
In Windows GDI+ è possibile archiviare una trasformazione affine in un oggetto Matrix . Poiché la terza colonna di una matrice che rappresenta una trasformazione affine è sempre (0, 0, 1), si specificano solo i sei numeri nelle prime due colonne quando si costruisce un oggetto Matrix . L'istruzione Matrix myMatrix(0.0f, 1.0f, -1.0f, 0.0f, 3.0f, 4.0f); costruisce la matrice illustrata nella figura precedente.

Trasformazioni composite

Una trasformazione composita è una sequenza di trasformazioni, una seguita dall'altra. Si considerino le matrici e le trasformazioni nell'elenco seguente:

• Matrice A Ruota di 90 gradi
• Scala matrice B per un fattore pari a 2 nella direzione x
• Matrice C Traduci 3 unità nella direzione y

Se si inizia con il punto (2, 1), rappresentato dalla matrice [2 1 1] e moltiplicato per A, B, C, il punto (2,1) subirà le tre trasformazioni nell'ordine elencato.

[2 1 1] ABC = [ -2 5 1]

Anziché archiviare le tre parti della trasformazione composita in tre matrici separate, è possibile moltiplicare A, B e C insieme per ottenere una singola matrice 3 × 3 che archivia l'intera trasformazione composita. Si supponga CHE ABC = D. Quindi un punto moltiplicato per D restituisce lo stesso risultato di un punto moltiplicato per A, quindi B, quindi C.

[2 1 1] D = [ –2 5 1]

La figura seguente mostra le matrici A, B, C e D.

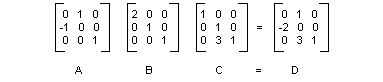
Il fatto che la matrice di una trasformazione composita possa essere formata moltiplicando le singole matrici di trasformazione, significa che qualsiasi sequenza di trasformazioni affine può essere archiviata in un singolo oggetto Matrix .

Nota

L'ordine di una trasformazione composita è importante. In generale, ruotare, quindi ridimensionare, quindi tradurre non è uguale alla scala, quindi ruotare, quindi tradurre. Analogamente, l'ordine della moltiplicazione della matrice è importante. In generale, ABC non è uguale a BAC.

 

La classe Matrix fornisce diversi metodi per la creazione di una trasformazione composita: Matrix::Multiply, Matrix::Rotate, Matrix::RotateAt, Matrix::Scale, Matrix::Shear e Matrix::Translate. Nell'esempio seguente viene creata la matrice di una trasformazione composita che ruota prima di 30 gradi, quindi viene ridimensionata per un fattore pari a 2 nella direzione y e quindi vengono convertite 5 unità nella direzione x.

Matrix myMatrix;
myMatrix.Rotate(30.0f);
myMatrix.Scale(1.0f, 2.0f, MatrixOrderAppend);
myMatrix.Translate(5.0f, 0.0f, MatrixOrderAppend);

La figura seguente mostra la matrice.