チュートリアル: Q# で量子乱数ジェネレーターを実装する

[アーティクル]
10/29/2024

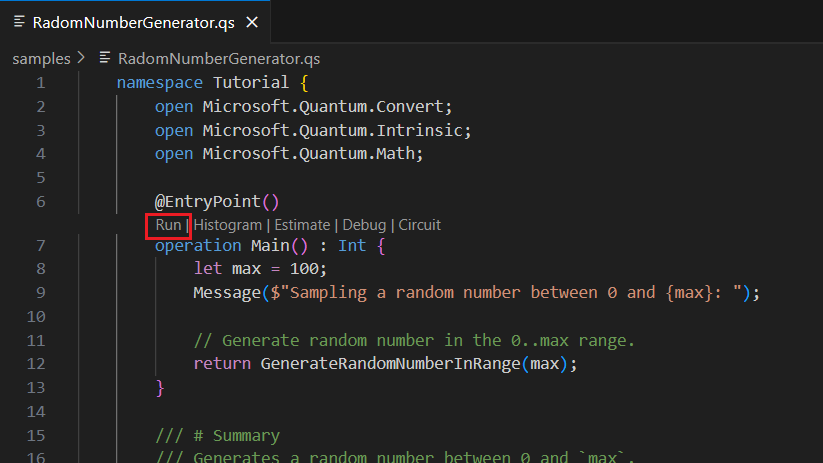
このチュートリアルでは、量子力学の性質を利用して乱数を生成する基本的な量子プログラム Q# を記述する方法について説明します。

このチュートリアルでは、次のことについて説明します。

プログラムを作成します Q# 。
プログラムの主要なコンポーネントを Q# 確認します。
問題のロジックを定義する。
従来の演算と量子演算を組み合わせて問題を解決する。
量子ビットと重ね合わせを使用して、量子乱数ジェネレーターを構築します。

ヒント

量子コンピューティングの取り組みを加速させる場合は、Azure Quantum Web サイトのユニークな機能である Azure Quantum を使用したコードを確認してください。ここでは、組Q#み込みのサンプルまたは独自Q#のプログラムを実行し、プロンプトから新しいQ#コードを生成し、1 回のクリックで VS Code for the Web でコードを開いて実行し、コピロットに量子コンピューティングに関する質問をすることができます。

前提条件

Azure Quantum の Copilot でコードサンプルを実行するには:
- Microsoft (MSA) メールアカウント。
Visual Studio Code でコードサンプルを開発して実行するには:
- 最新バージョンの Visual Studio Code または VS Code on the Web を開きます。
- Azure Quantum Development Kit 拡張機能の最新バージョン。インストールの詳細については、VS Code への QDK のインストールを参照してください。
- Jupyter Notebook を使用する場合は、Python と Jupyter 拡張機能、および最新qsharpの Python パッケージもインストールする必要があります。これを行うには、ターミナルを開き、次のコマンドを実行します。
```
$ pip install --upgrade  qsharp
```

問題を定義する

従来のコンピューターでは、乱数ではなく、"擬似乱数" が生成されます。擬似乱数ジェネレーターでは、"シード" と呼ばれる初期値に基づいて、決定論的な数列が生成されます。ランダムな値に近づけるために、このシードは CPU のクロックの現在時刻になることがよくあります。

一方、量子コンピューターは真の乱数を生成できます。これは、重ね合わせにおける量子ビットの測定が確率的プロセスであるためです。測定の結果はランダムであり、結果を予測する方法はありません。これが量子乱数ジェネレーターの基本原則です。

量子ビットは、重ね合わせ可能な量子情報の単位です。測定された場合、量子ビットは 0 の状態または 1 の状態のいずれかになります。ただし測定の前において、量子ビットの状態は測定で 0 または 1 を読み取る ”可能性” を表わします。

まず、0 などの基礎状態で量子ビットを取得します。乱数ジェネレーターの最初の手順は、Hadmard 演算を使用して量子ビットを等しい重ね合わせに配置することです。この状態を測定すると、各結果の確率が 50% の 0 または 1 が生じ、真にランダムなビットになります。

重ね合わせでの量子ビットの測定後に何が得られるかを知る方法はなく、コードが呼び出されるたびに結果は異なる値になります。しかし、この動作をどのように使えば、より大きな乱数を生成できるのでしょうか?

このプロセスを 4 回繰り返すと、次のような 2 進数の数列が生成されます。

$${0, 1, 1, 0}$$

これらのビットをビット文字列に連結 (結合) すると、より大きな数値を使用できます。この例では、ビットシーケンス ${0110}$ は 10 進数の 6 に相当します。

$${0110_{\ 2 進} \equiv 6_{\ 10 進}}$$

このプロセスを何度も繰り返すと、複数のビットを組み合わせてあらゆる大きな数値を形成できます。この方法を使用すると、安全なパスワードとして使用する数値を作成できます。これは、ハッカーが一連の測定値の結果を特定できないことを確認できるためです。

乱数ジェネレーターのロジックを定義する

乱数ジェネレーターのロジックの概要を説明します。

生成する最大数として max を定義します。
生成する必要がある乱数ビットの数を定義します。これは、ビット数を計算することによって行われ、 nBits最大 maxで整数を表す必要があります。
長さが nBits の乱数ビット文字列を生成します。
ビット文字列が max より大きい数値を表す場合、ステップ 3 に戻ります。
それ以外の場合、プロセスは終了です。生成された数値を整数として返します。

例として、max を 12 に設定します。つまり、パスワードとして使用する最大の数は 12 です。

0 から 12 までの数値を表すには、${\lfloor ln(12) / ln(2) + 1 \rfloor}$ ビット、つまり 4 ビットが必要です。任意の整数を受け取り、それを表すために必要なビット数を返す組み込み関数 BitSizeIを使用できます。

たとえば、ビット文字列 ${1101_{\ binary}}$ を生成したとします。これは ${13_{\ decimal}}$ と等価です。 13 は 12 より大きいため、この処理を繰り返します。

次に、ビット文字列 ${0110_{\ binary}}$ を生成したとします。これは ${6_{\ decimal}}$ と等価です。 6 は 12 未満であるため、この処理を終了します。

量子乱数ジェネレーターは、パスワードとして数値 6 を返します。実際には、最大としてより大きな数値を設定します。小さい数値だと、使用可能な全パスワードを試すだけで簡単に解読できるためです。実際、パスワードの推測や解析をより困難にするために、ASCII コードを使用してバイナリをテキストに変換し、数字、記号、および大文字と小文字が混在した文字を使用してパスワードを生成することもできます。

ランダムビットジェネレーターを書き込む

最初の手順では、ランダムビットを Q# 生成する操作を記述します。この操作は、乱数ジェネレーターの構成要素の 1 つになります。

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

次に、新しいコードを見てみます。

GenerateRandomBit 操作を定義します。これには入力が不要であり、型 Result の値が生成されます。 Result 型は測定の結果を表し、Zero または One の 2 つの値を使用できます。
キーワードを使用して 1 つの量子ビットを use 割り当てます。割り当てられると、量子ビットは常に |0〉状態になります。
この演算を H 使用して、量子ビットを等しい重ね合わせに配置します。
演算を M 使用して量子ビットを測定し、測定値 (Zero または One) を返します。
この操作を Reset 使用して、量子ビットを |0〉状態にリセットします。

H 操作を使用して量子ビットを重ね合わせに入れ、それを M 操作で測定することで、コードを呼び出すたびに結果は異なる値になります。

Bloch 球を Q# 使用してコードを視覚化する

ブロッホ球では、北極は古典的な値 0 を表し、南極は古典的な値 1 を表します。重ね合わせは球上の点で表わすことができます (矢印で表わされています)。矢印の端が極に近づけば近づくほど、測定時、その極に割り当てられる古典的な値にキュービットがなる確率が高くなります。たとえば、次の図の矢印で表わされているキュービットの状態では、測定したとき、値 0 が与えられる可能性が高くなります。

この表現を利用し、コードの動作を視覚化できます。

まず、|0〉状態で初期化された量子ビットから始めて、0 と 1 の確率が同じ等しい重ね合わせを作成する操作を適用Hします。
次に、量子ビットを測定し、出力を保存します。

測定の結果はランダムであり、0 と 1 を測定する確率が同じであるため、完全にランダムなビットを取得しています。この操作を複数回呼び出し、整数を作成できます。たとえば、操作を 3 回呼び出してランダムビットを 3 つ取得する場合、ランダムの 3 ビット数 (つまり、0 から 7 までの乱数) を構築できます。

完全な乱数ジェネレーターを書き込む

まず、必要な名前空間を標準ライブラリからプログラムに Q# インポートする必要があります。コンパイラはQ#多くの一般的な関数と操作を自動的に読み込みますが、完全な乱数ジェネレーターの場合は、2 つのQ#名前空間Microsoft.Quantum.MathMicrosoft.Quantum.Convertからいくつかの追加の関数と操作が必要です。
```
import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;
```
次に、操作を定義します GenerateRandomNumberInRange 。この演算は GenerateRandomBit 演算を繰り返し呼び出して、ビット文字列を構築します。
```
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}
```
少し時間を取って新しいコードを確認してみましょう。
- 最大 max の整数を表現するために必要なビット数を計算する必要があります。名前空間のMicrosoft.Quantum.Math関数はBitSizeI、整数を表すために必要なビット数に変換します。
- SampleRandomNumberInRange 演算は for ループを使用して、max 以下の乱数を生成するまで乱数を生成します。 for ループは、他のプログラミング言語の for ループとまったく同じように動作します。
- 変数 bits は変更可能な変数です。変更可能な変数は、計算中に変更できる変数です。 set ディレクティブを使用して、変更可能な変数の値を変更することができます。
- 関数は ResultArrayAsInt 、既定 Microsoft.Quantum.Convert の名前空間から、ビット文字列を正の整数に変換します。
最後に、エントリポイントをプログラムに追加します。既定では、コンパイラは Q# 操作を Main 検索し、そこで処理を開始します。この操作を GenerateRandomNumberInRange 呼び出して、0 ~ 100 の乱数を生成します。
```
operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}
```
let ディレクティブは、計算中に変更されない変数を宣言します。ここでは、最大値を 100 として定義します。

操作の詳細Mainについては、「エントリポイント」を参照してください。
乱数ジェネレーターの完全なコードは次のとおりです。

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using a Hadamard operation
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;
}

乱数ジェネレータープログラムを実行する

このプログラムは、Azure Quantum の Copilot で、Visual Studio Code ではスタンドアロン Q# アプリケーションとして、または Python ホストプログラムを使用して実行できます。

Azure Quantum で Copilot を使用してコードを Q# 無料でテストできます。必要なのは Microsoft (MSA) メールアカウントのみです。 Azure Quantum の Copilot の詳細については、「Azure Quantum の探索」を参照してください。

ブラウザーで Azure Quantum で Copilot を開きます。

次のコードをコピーしてコードエディターに貼り付けます。

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

実行するショットの数を選択し、[実行] を選択します。
結果はヒストグラムと結果フィールドに表示されます。
[コードの説明] を選択して、コードを説明するように Copilot に求めるメッセージを表示します。

ヒント

Azure Quantum の Copilot から、コードエディターの右上隅にある VS Code ロゴボタンを選択することで、VS Code for the Web でプログラムを開くことができます。

Visual Studio Code を開き、[ファイル] > [新しいテキストファイル] を選んで新しいファイルを作成します。
このファイルを RandomNumberGenerator.qs として保存します。このファイルには、プログラムのコードが Q# 含まれます。

ファイル内の次のコードを RandomNumberGenerator.qs コピーします。


import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;
    Message($"Sampling a random number between 0 and {max}: ");

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

プログラムを実行する前に、プロファイルを無制限に設定targetする必要があります。 [表示 ] -> [コマンドパレット] を選択し、[QIR] をQ#検索し、[Azure Quantum QIR target プロファイルを設定する] を選択して、[無制限] を選択Q#します。
プログラムを実行するには、右上の再生アイコンドロップダウンから [ファイルの実行Q#] を選択し、前のコマンドの一覧から [実行] を選択するか、Ctrl キーを押しながら F5 キーをMain()押します。プログラムは、既定の Main() シミュレーターで操作を実行します。
出力がデバッグコンソールに表示されます。
プログラムを再度実行すると、異なる結果が表示されます。

Note

プロファイルが target Unrestricted に設定されていない場合は、プログラムの実行時にエラーが発生します。

頻度ヒストグラムをプロットする

量子プログラムを複数回実行して得られた結果の分布を視覚化してみましょう。頻度ヒストグラムは、これらの結果の確率分布を視覚化するのに役立ちます。

[表示 ] -> [コマンドパレット] を選択し、「ヒストグラム」と入力します。これにより、[ファイルの実行とヒストグラムのQ#表示] オプションが表示されます。前のコマンドの一覧からヒストグラムをMain()選択することもできます。ヒストグラムウィンドウを開くには、このオプションを Q# 選択します。
プログラムを実行するショットの数 (100 ショットなど) を入力し、Enter キーを押します。ヒストグラムがヒストグラムウィンドウに Q# 表示されます。
ヒストグラムの各バーは、考えられる結果に対応し、その高さは結果が観察される回数を表します。ヒストグラムを実行するたびに異なる結果の数が異なる場合があります。

ヒント

マウススクロールホイールまたはトラックパッドジェスチャを使用して、ヒストグラムをズームできます。拡大すると、スクロール中に 'Alt' キーを押してグラフをパンできます。
バーを選択すると、その結果の割合が表示されます。
左上 の設定アイコン を選択して、オプションを表示します。上位 10 件の結果、上位 25 件の結果、またはすべての結果を表示できます。また、結果を高から低、低から高に並べ替えることもできます。

VS Code で、[表示] > [コマンドパレット] を選択して、[作成: 新しい Jupyter Notebook] を選択します。
最初のセルで、Python コードに qsharp パッケージをインポートします。
```
import qsharp
```

Q#量子乱数ジェネレータープログラムのコードを追加します。これを行うには、マジックコマンドを %%qsharp 使用します。このコマンドでは、 %%qsharp ノートブックのセルが型から型 Python に変更されることに注意してください Q#。このコードを 2 番目のセルにコピーします。

%%qsharp

import Microsoft.Quantum.Convert.*;
import Microsoft.Quantum.Math.*;

operation Main() : Int {
    let max = 100;

    // Generate random number in the 0..max range.
    return GenerateRandomNumberInRange(max);
}

/// # Summary
/// Generates a random number between 0 and `max`.
operation GenerateRandomNumberInRange(max : Int) : Int {
    // Determine the number of bits needed to represent `max` and store it
    // in the `nBits` variable. Then generate `nBits` random bits which will
    // represent the generated random number.
    mutable bits = [];
    let nBits = BitSizeI(max);
    for idxBit in 1..nBits {
        set bits += [GenerateRandomBit()];
    }
    let sample = ResultArrayAsInt(bits);

    // Return random number if it is within the requested range.
    // Generate it again if it is outside the range.
    return sample > max ? GenerateRandomNumberInRange(max) | sample;
}

/// # Summary
/// Generates a random bit.
operation GenerateRandomBit() : Result {
    // Allocate a qubit.
    use q = Qubit();

    // Set the qubit into superposition of 0 and 1 using the Hadamard 
    // operation `H`.
    H(q);

    // At this point the qubit `q` has 50% chance of being measured in the
    // |0〉 state and 50% chance of being measured in the |1〉 state.
    // Measure the qubit value using the `M` operation, and store the
    // measurement value in the `result` variable.
    let result = M(q);

    // Reset qubit to the |0〉 state.
    // Qubits must be in the |0〉 state by the time they are released.
    Reset(q);

    // Return the result of the measurement.
    return result;

    // Note that Qubit `q` is automatically released at the end of the block.
}

最後に、コードを実行します。同じシミュレーションは、個別に何度も実行できます。各独立したシミュレーションは、"ショット" と呼ばれます。たとえば、シミュレーションを 100 回実行してみましょう。
```
results = qsharp.run("Main()", shots=100)
print(results)
```

Note

このコードスニペットは現在、使用可能な Azure Quantum ハードウェアでは実行されません。呼び出し可能な場合targetsは、完全なResultArrayAsInt計算プロファイルを持つ QPU が必要です。

Q# のその他のチュートリアルを確認します。

量子エンタングルメントは、量子ビットを操作および測定し、重ね合わせとエンタングルメントの効果を示すプログラムを記述 Q# する方法を示します。
グローバーの検索アルゴリズムは、グローバーの検索アルゴリズムを Q# 使用するプログラムを記述する方法を示しています。
Quantum フーリエ変換では、特定の量子ビットに直接対処するプログラムを Q# 記述する方法について説明します。
Quantum Katas は、量子コンピューティングとプログラミングの要素を同時に教えることを目的とした、自習型のチュートリアルとQ#プログラミング演習です。

次の方法で共有

チュートリアル: Q# で量子乱数ジェネレーターを実装する

前提条件

問題を定義する

乱数ジェネレーターのロジックを定義する

ランダムビットジェネレーターを書き込む

Bloch 球を Q# 使用してコードを視覚化する

完全な乱数ジェネレーターを書き込む

乱数ジェネレータープログラムを実行する

頻度ヒストグラムをプロットする

フィードバック

その他のリソース

次の方法で共有

チュートリアル: Q# で量子乱数ジェネレーターを実装する

前提条件

問題を定義する

乱数ジェネレーターのロジックを定義する

ランダム ビット ジェネレーターを書き込む

Bloch 球を Q# 使用してコードを視覚化する

完全な乱数ジェネレーターを書き込む

乱数ジェネレータープログラムを実行する

関連するコンテンツ

フィードバック

その他のリソース

ランダムビットジェネレーターを書き込む