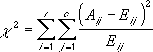Метод WorksheetFunction.ChiTest (Excel)

Возвращает тест на независимость.

Важно!

Эта функция была заменена одной или несколькими новыми функциями, которые могут обеспечить повышенную точность и имена которых лучше отражают их использование. Эта функция по-прежнему доступна для совместимости с более ранними версиями Excel. Однако если обратная совместимость не требуется, следует рассмотреть возможность использования новых функций, так как они более точно описывают их функциональность.

Дополнительные сведения о новой функции см. в разделе метод ChiSq_Test .

Синтаксис

expression. ChiTest (Arg1, Arg2)

Выражение Переменная, представляющая объект WorksheetFunction .

Параметры

Имя	Обязательный или необязательный	Тип данных	Описание
Arg1	Обязательный	Variant	Диапазон данных, содержащих наблюдения для проверки ожидаемых значений.
Arg2	Обязательный	Variant	Диапазон данных, содержащий отношение продукта итогов строк и итогов столбцов к общему итогу.

Возвращаемое значение

Double

Замечания

ChiTest возвращает значение из распределения хи-квадрата (12) для статистики и соответствующих степеней свободы. Используйте тесты 12, чтобы определить, проверяются ли гипотезные результаты экспериментом.

Если actual_range и expected_range имеют разное количество точек данных, ChiTest возвращает значение ошибки #N/A.

Тест 12 сначала вычисляет статистику α2 по следующей формуле, где:

• Aij = фактическая частота в i-й строке, j-й столбец
• Eij = ожидаемая частота в i-й строке, j-й столбец
• r = число или строк
• c = количество столбцов

Низкое значение null2 является показателем независимости. Как видно из формулы, α2 всегда положительно или 0, а равно 0, только если Aij = Eij для каждого i,j.

ChiTest возвращает вероятность того, что значение статистики 12, по крайней мере, такое же высокое, как значение, вычисленное по предыдущей формуле, могло произойти случайно при предположении о независимости. При вычислении этой вероятности ChiTest использует распределение α2 с соответствующим числом степеней свободы, df.

• Если r > 1 и c > 1, то df = (r - 1)(c - 1).
• Если r = 1 и c > 1, то df = c - 1.
• Если r > 1 и c = 1, то df = r - 1.
• r = c = 1 не допускается и создает ошибку.

Использование ChiTest является наиболее подходящим, когда Eij не слишком мал. Некоторые статистики предполагают, что каждый Эйдж должен быть больше или равен 5.

Поддержка и обратная связь

Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.