Ескертпе
Бұл бетке кіру үшін қатынас шегін айқындау қажет. Жүйеге кіруді немесе каталогтарды өзгертуді байқап көруге болады.
Бұл бетке кіру үшін қатынас шегін айқындау қажет. Каталогтарды өзгертуді байқап көруге болады.
Используйте неаффинные преобразования для поворота трехмерных объектов в трехмерном пространстве.
Одним из распространенных применений неаффинных преобразований является имитация поворота 2D-объекта в трехмерном пространстве:

Это задание предполагает работу с трехмерными поворотами, а затем производным от аффинного SKMatrix преобразования, выполняющего эти трехмерные повороты.
Трудно разработать это SKMatrix преобразование исключительно в двух измерениях. Задание становится гораздо проще, когда эта матрица 3-к-3 является производным от матрицы 4-к-4, используемой в трехмерной графике. SkiaSharp включает SKMatrix44 класс для этой цели, но некоторый фон в трехмерной графике необходим для понимания трехмерных поворотов и матрицы преобразования 4-к-4.
Трехмерная система координат добавляет третью ось под названием Z. Концептуально ось Z находится в правых углах экрана. Точки координат в трехмерном пространстве указываются с тремя числами: (x, y, z). В 3D-системе координат, используемой в этой статье, увеличение значений X справа и увеличение значений Y опускаются так же, как в двух измерениях. Увеличение положительных значений Z выходит из экрана. Источник — левый верхний угол, как и в 2D-графике. Экран можно рассматривать как плоскость XY с осью Z в правых углах этой плоскости.
Это называется левой системой координат. Если вы указываете указатель на указатель на левую руку в направлении положительных координат X (справа), а средний палец в направлении увеличения координат Y (вниз), то ваш пальцем в направлении увеличения координат Z — вытягивается с экрана.
В трехмерной графике преобразования основаны на матрице 4–4. Ниже приведена матрица удостоверений 4-4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
При работе с матрицей 4–4 удобно идентифицировать ячейки со своими номерами строк и столбцов:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Однако класс SkiaSharp Matrix44 немного отличается. Единственным способом установки или получения отдельных значений SKMatrix44 ячеек является использование Item индексатора. Индексы строк и столбцов основаны на нулях, а не на основе одного, а строки и столбцы переключаются. Доступ к ячейке M14 на приведенной выше схеме осуществляется с помощью индексатора [3, 0] в объекте SKMatrix44 .
В трехмерной графической системе трехмерная точка (x, y, z) преобразуется в матрицу 1 на 4 для умножения на матрицу преобразования 4-на-4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Аналогичные 2D-преобразованиям, которые происходят в трех измерениях, предполагается, что трехмерные преобразования выполняются в четырех измерениях. Четвертое измерение называется W, и предполагается, что трехмерное пространство существует в пределах 4D-пространства, где координаты W равны 1. Формулы преобразования приведены следующим образом:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Очевидно, что из формул преобразования ячейки M11, M22M33 являются факторами масштабирования в направлениях X, Y и Z, а M41M42M43 также являются факторами перевода в направлениях X, Y и Z.
Чтобы преобразовать эти координаты обратно в трехмерное пространство, где W равно 1, координаты x', y', и z все разделены на w':
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Это разделение по w' обеспечивает перспективу в трехмерном пространстве. Если w' равен 1, то перспектива не возникает.
Повороты в трехмерном пространстве могут быть довольно сложными, но простейшие повороты находятся вокруг осей X, Y и Z. Поворот угловой α вокруг оси X — это матрица:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Значения X остаются неизменными при выполнении этого преобразования. Поворот вокруг оси Y оставляет значения Y без изменений:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
Поворот вокруг оси Z совпадает с трехмерной графикой:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Направление поворота подразумевается рукой системы координат. Это левая система, поэтому если вы указываете пальцем левой руки на увеличение значений для определенной оси — справа для поворота вокруг оси X, вниз для поворота вокруг оси Y и к вам для поворота вокруг оси Z , то кривая других пальцев указывает направление поворота для положительных углов.
SKMatrix44 имеет обобщенные статические CreateRotation и CreateRotationDegrees методы, позволяющие указать ось, вокруг которой происходит поворот:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Для поворота вокруг оси X задайте для первых трех аргументов значение 1, 0, 0. Для поворота вокруг оси Y задайте для них значение 0, 1, 0 и для поворота вокруг оси Z, задайте для них значение 0, 0, 1.
Четвертый столбец 4-к-4 предназначен для перспективы. Нет SKMatrix44 методов для создания преобразований перспективы, но вы можете создать его самостоятельно с помощью следующего кода:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
Причина имени depth аргумента будет очевидна в ближайшее время. Этот код создает матрицу:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Формулы преобразования приводят к следующему вычислению w':
w' = –z / depth + 1
Это позволяет уменьшить координаты X и Y, если значения Z меньше нуля (концептуально за плоскости XY) и увеличить координаты X и Y для положительных значений Z. Когда координата depthZ равна нулю, а координаты становятся бесконечными. Трехмерные графические системы создаются вокруг метафоры камеры, а depth значение здесь представляет расстояние камеры от источника системы координат. Если графический объект имеет координату Z, которая является depth единицами из источника, она концептуально касается объектива камеры и становится бесконечно большой.
Помните, что вы, вероятно, будете использовать это perspectiveMatrix значение в сочетании с матрицами поворота. Если вращаемый графический объект имеет координаты X или Y больше depth, то поворот этого объекта в трехмерном пространстве, скорее всего, будет включать координаты Z больше, чем depth. Это необходимо избежать! При создании perspectiveMatrix необходимо задать depth достаточно большое значение для всех координат в графическом объекте независимо от того, как он поворачивается. Это гарантирует, что никакого деления на ноль никогда не существует.
Объединение трехмерных поворотов и перспективы требует умножения 4 на 4 матрицы вместе. Для этого SKMatrix44 определяет методы объединения. Если A и B являются SKMatrix44 объектами, следующий код задает A равно A × B:
A.PostConcat(B);
Если матрица преобразования 4–4 используется в 2D-графической системе, она применяется к 2D-объектам. Эти объекты являются неструктурированными, и предполагается, что координаты Z равны нулю. Умножение преобразования немного проще, чем показанное ранее преобразование:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Это значение 0 для z приводит к формулам преобразования, которые не включают ячейки в третьей строке матрицы:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Кроме того, координата Z здесь не имеет значения. Если трехмерный объект отображается в трехмерной графической системе, он свернут в двухмерный объект, игнорируя значения координат Z. Формулы преобразования на самом деле являются двумя:
x" = x' / w'
y" = y' / w'
Это означает, что третью строку и третий столбец матрицы 4-4 можно игнорировать.
Но если это так, почему матрица 4-к-4 даже необходима в первую очередь?
Хотя третья строка и третий столбец 4-к-4 не имеют значения для двухмерных преобразований, третья строка и столбец играют роль до этого, когда различные SKMatrix44 значения умножаются вместе. Например, предположим, что вы умножаете поворот вокруг оси Y с преобразованием перспективы:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
В продукте ячейка M14 теперь содержит значение перспективы. Если вы хотите применить эту матрицу к объектам 2D, третья строка и столбец удаляются, чтобы преобразовать ее в матрицу с 3 по 3:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Теперь его можно использовать для преобразования 2D-точки:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Формулы преобразования:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Теперь разделите все на z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Когда 2D-объекты поворачиваются с положительным углом вокруг оси Y, то положительные значения X отступают на фон, а отрицательные значения X приходят на передний план. Значения X, кажется, приближаются к оси Y (которая управляется значением косинуса), так как координаты от оси Y становятся меньше или больше, когда они перемещаются дальше от средства просмотра или ближе к средству просмотра.
При использовании SKMatrix44выполните все трехмерные операции поворота и перспективы путем умножения различных SKMatrix44 значений. Затем можно извлечь двухмерную матрицу 3-к-3 из матрицы 4-к-4 с помощью Matrix свойства SKMatrix44 класса. Это свойство возвращает знакомое SKMatrix значение.
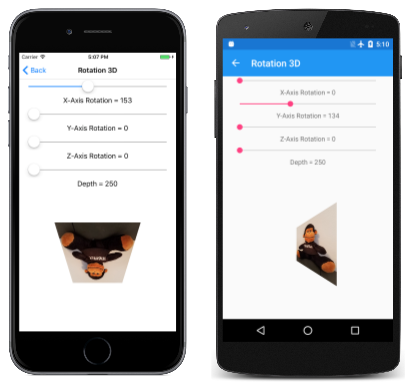
Страница поворота 3D позволяет экспериментировать с трехмерной сменой. Файл Rotation3DPage.xaml создает четыре ползунка, чтобы задать поворот вокруг осей X, Y и Z, а также задать значение глубины:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Обратите внимание, что инициализировано depthSlider со значением Minimum 250. Это означает, что 2D-объект, вращаемый здесь, имеет координаты X и Y, ограниченные кругом, определенным радиусом 250 пикселей вокруг источника. Любой поворот этого объекта в трехмерном пространстве всегда приводит к значению координат менее 250.
Файл Rotation3DPage.cs программной части загружается в растровом рисунке, который составляет 300 пикселей:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Если трехмерный преобразование сосредоточено на этом растровом рисунке, координаты X и Y находятся в диапазоне от –150 до 150, а угловые — 212 пикселей от центра, поэтому все находится в радиусе 250 пикселей.
Обработчик PaintSurface создает SKMatrix44 объекты на основе ползунка и умножает их вместе с помощью PostConcat. Значение SKMatrix , извлеченное из конечного SKMatrix44 объекта, окружено преобразованиями, чтобы центрировать поворот в центре экрана:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
При эксперименте с четвертым ползунок вы заметите, что различные параметры глубины не перемещают объект дальше от средства просмотра, а вместо этого изменяют степень эффекта перспективы:
Анимированный поворот 3D также используется SKMatrix44 для анимации текстовой строки в трехмерном пространстве. Объект, textPaint заданный в качестве поля, используется в конструкторе для определения границ текста:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
Переопределение OnAppearing определяет триAnimationXamarin.Formsобъекта для анимации xRotationDegreesyRotationDegreesполей и zRotationDegrees полей с разными скоростями. Обратите внимание, что для периодов этих анимаций заданы простые числа (5 секунд, 7 секунд и 11 секунд), поэтому общая комбинация повторяется только каждые 385 секунд или более 10 минут:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Как и в предыдущей программе, PaintCanvas обработчик создает SKMatrix44 значения для поворота и перспективы и умножает их вместе:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Этот трехмерный поворот окружен несколькими 2D-преобразованиями для перемещения центра поворота в центр экрана и масштабирования размера текстовой строки таким образом, чтобы она была той же шириной, что и экран: