VB.Net - Random Maze Games
Overview
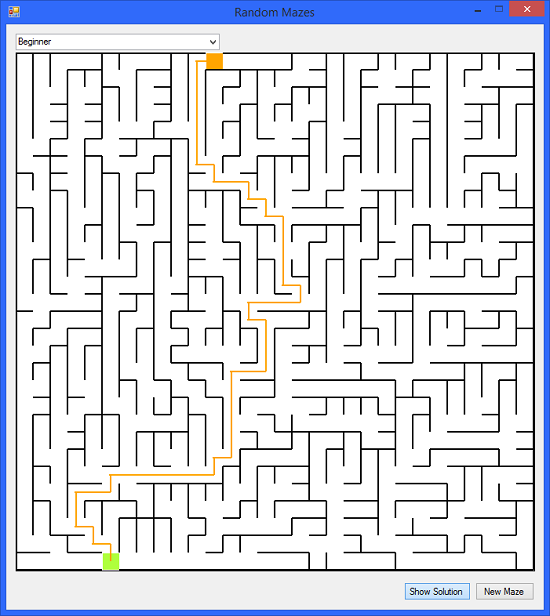
This is a maze solving game, with a maze overlay drawn on an extended (restricted) DataGridView. The DataGridView only accepts arrow key input.
The mazes are created in conjunction with a 2D array, and arrow key movement through the DataGridView is limited to clear paths. Navigation is blocked where walls are drawn. The solver part of the game finds and draws a path from the start cell to the end cell.
The game has three levels - Beginner, Intermediate, and Advanced, which translates to 30*30 cells, 40*40 cells, and 50*50 cells...
Creating a Prim's Algorithm maze
When creating a random maze, each cell starts with four walls. Given a starting cell, the maze is created with each new cell being a random spur from a random branch of the existing maze. Walls between the random maze cell and the new cell are removed. This new cell is then added to the existing maze, and the process repeats until all of the cells in the grid have been visited.
Public Sub createMaze(ByVal m As Integer, ByVal randomNumber As Random)
'create new maze
ReDim Grid.Cells(m - 1)
For c As Integer = 0 To m - 1
ReDim Grid.Cells(c)(m - 1)
For r As Integer = 0 To m - 1
Grid.Cells(c)(r) = New Grid.cellDetails
Next
Next
For c As Integer = 0 To Grid.Cells.GetUpperBound(0)
For r As Integer = 0 To Grid.Cells(0).GetUpperBound(0)
Grid.Cells(c)(r).visited = False
Grid.Cells(c)(r).NorthWall = True
Grid.Cells(c)(r).SouthWall = True
Grid.Cells(c)(r).WestWall = True
Grid.Cells(c)(r).EastWall = True
Next
Next
'Stop
Dim maze As New List(Of Point)
Dim unvisited As Integer = m ^ 2
Grid.startPoint = New Point(randomNumber.Next(0, m), m - 1)
Grid.Cells(Grid.startPoint.X)(m - 1).SouthWall = False
maze.Add( New Point(Grid.startPoint.X, m - 1))
unvisited -= 1
While unvisited > 0
Dim p As Point = maze(randomNumber.Next(0, maze.Count))
Dim choice As New List(Of Point)
If p.X > 0 And p.X < m - 1 Then 'c
If p.Y > 0 And p.Y < m - 1 Then 'r
choice.AddRange( New Point() {New Point(p.X - 1, p.Y), New Point(p.X, p.Y - 1), New Point(p.X + 1, p.Y), New Point(p.X, p.Y + 1)}) 'l,t,r,b
ElseIf p.Y = 0 Then
choice.AddRange( New Point() {New Point(p.X - 1, p.Y), New Point(p.X + 1, p.Y), New Point(p.X, p.Y + 1)}) 'l,r,b
ElseIf p.Y = m - 1 Then
choice.AddRange( New Point() {New Point(p.X - 1, p.Y), New Point(p.X, p.Y - 1), New Point(p.X + 1, p.Y)}) 'l,t,r
End If
ElseIf p.X = 0 Then 'c
If p.Y > 0 And p.Y < m - 1 Then 'c
choice.AddRange( New Point() {New Point(p.X, p.Y - 1), New Point(p.X + 1, p.Y), New Point(p.X, p.Y + 1)}) 't,r,b
ElseIf p.Y = 0 Then
choice.AddRange( New Point() {New Point(p.X + 1, p.Y), New Point(p.X, p.Y + 1)}) 'r,b
ElseIf p.Y = m - 1 Then
choice.AddRange( New Point() {New Point(p.X, p.Y - 1), New Point(p.X + 1, p.Y)}) 't,r
End If
ElseIf p.X = m - 1 Then 'c
If p.Y > 0 And p.Y < m - 1 Then
choice.AddRange( New Point() {New Point(p.X - 1, p.Y), New Point(p.X, p.Y - 1), New Point(p.X, p.Y + 1)}) 'l,t,b
ElseIf p.Y = 0 Then
choice.AddRange( New Point() {New Point(p.X - 1, p.Y), New Point(p.X, p.Y + 1)}) 'l,b
ElseIf p.Y = m - 1 Then
choice.AddRange( New Point() {New Point(p.X - 1, p.Y), New Point(p.X, p.Y - 1)}) 'l,t
End If
End If
choice.RemoveAll( Function (pt) Grid.Cells(pt.X)(pt.Y).visited)
If choice.Count = 0 Then Continue While
Dim p2 As Point = choice(randomNumber.Next(0, choice.Count))
If p.X = p2.X And p2.Y < p.Y Then
If Grid.Cells(p.X)(p.Y).NorthWall Then
Grid.Cells(p.X)(p.Y).NorthWall = False
Grid.Cells(p2.X)(p2.Y).SouthWall = False
Grid.Cells(p2.X)(p2.Y).visited = True
unvisited -= 1
maze.Add( New Point(p2.X, p2.Y))
Else
Continue While
End If
ElseIf p.X = p2.X And p2.Y > p.Y Then
If Grid.Cells(p.X)(p.Y).SouthWall Then
Grid.Cells(p.X)(p.Y).SouthWall = False
Grid.Cells(p2.X)(p2.Y).NorthWall = False
Grid.Cells(p2.X)(p2.Y).visited = True
unvisited -= 1
maze.Add(p2)
Else
Continue While
End If
ElseIf p.X > p2.X And p2.Y = p.Y Then
If Grid.Cells(p.X)(p.Y).WestWall Then
Grid.Cells(p.X)(p.Y).WestWall = False
Grid.Cells(p2.X)(p2.Y).EastWall = False
Grid.Cells(p2.X)(p2.Y).visited = True
unvisited -= 1
maze.Add(p2)
Else
Continue While
End If
ElseIf p.X < p2.X And p2.Y = p.Y Then
If Grid.Cells(p.X)(p.Y).EastWall Then
Grid.Cells(p.X)(p.Y).EastWall = False
Grid.Cells(p2.X)(p2.Y).WestWall = False
Grid.Cells(p2.X)(p2.Y).visited = True
unvisited -= 1
maze.Add(p2)
Else
Continue While
End If
End If
End While
End Sub
Solving with Recursive BackTracking
Given a starting cell, each cell N, E, S, W of the starting cell (where not out of bounds, and the cell hasn't already been visited and processed) is recursively processed to assess whether it is a valid path. For each of these (potentially) four cells, the process is repeated, until a processed cell is out of bounds, in which case the solver returns false, or, a processed cell is the target cell (end point), in which case the solver returns true. Any cell returning false is discarded. Those cells returning true are added to the solution list in reverse order - end cell to start cell.
Public Function solveMaze(ByVal m As Integer, ByVal xPos As Integer, ByVal yPos As Integer, ByVal alreadySearched(,) As Boolean, ByVal solution As List(Of Point)) As Boolean
Dim correctPath As Boolean = False
'should the computer check this cell
Dim shouldCheck As Boolean = True
'Check for out of boundaries
If xPos >= m OrElse xPos < 0 OrElse yPos >= m OrElse yPos < 0 Then
shouldCheck = False
Else
'Check if at finish
If New Point(xPos, yPos) = Grid.endPoint Then
correctPath = True
shouldCheck = False
End If
'Check if previously searched
If alreadySearched(xPos, yPos) Then
shouldCheck = False
End If
End If
'Search the cell
If shouldCheck Then
'mark cell as searched
alreadySearched(xPos, yPos) = True
'Check right cell
correctPath = correctPath Or If(Grid.Cells(xPos)(yPos).EastWall = False, solveMaze(m, xPos + 1, yPos, alreadySearched, solution), False)
'Check down cell
correctPath = correctPath Or If(Grid.Cells(xPos)(yPos).SouthWall = False, solveMaze(m, xPos, yPos + 1, alreadySearched, solution), False)
'check left cell
correctPath = correctPath Or If(Grid.Cells(xPos)(yPos).WestWall = False, solveMaze(m, xPos - 1, yPos, alreadySearched, solution), False)
'check up cell
correctPath = correctPath Or If(Grid.Cells(xPos)(yPos).NorthWall = False, solveMaze(m, xPos, yPos - 1, alreadySearched, solution), False)
End If
'add cell to solution path
If correctPath Then
solution.Add(New Point(xPos, yPos))
End If
Return correctPath
End Function
Conclusion
Using a proven predefined algorithm, it's easy to create Random Mazes.
Analyzing these Mazes with a recursive technique quickly finds the shortest clear path from start point to end point.
This game works through the combined use of a restricted DataGridView and two 2D arrays...
Articles related to game programming
VB.Net - WordSearch
VB.Net - Vertex
VB.Net - Perspective
VB.Net - MasterMind
VB.Net - OOP BlackJack
VB.Net - Numbers Game
VB.Net - HangMan
Console BlackJack - VB.Net | C#
TicTacToe - VB.Net | C#
OOP Sudoku - VB.Net | C#
OctoWords VB.Net | C#
OOP Buttons Guessing Game VB.Net | C#
OOP Tangram Shapes Game VB.Net | C#
VB.Net - Three-card Monte
VB.Net - Pascal's Pyramid
VB.Net - Split Decisions
(Office) Wordsearch Creator
VB.Net - Event Driven Programming - LockWords Game
C# - Crack the Lock
VB.Net - Totris
Download
See Also
Creating a Prim's Algorithm maze
Solving with Recursive BackTracking