hll()(집계 함수)
적용 대상: ✅Microsoft Fabric✅Azure Data Explorer✅Azure Monitor✅Microsoft Sentinel
이 hll() 함수는 값 집합의 고유 값 수를 예측하는 방법입니다. 함수를 사용하여 dcount 데이터 그룹에 대한 요약 연산자 내에서 집계에 대한 중간 결과를 계산하여 이 작업을 수행합니다.
기본 알고리즘(H yperL ogLog) 및 추정 정확도에 대해 알아봅니다.
참고 항목
이 함수는 summarize 연산자와 함께 사용됩니다.
팁
- hll_merge 함수를 사용하여 여러
hll()함수의 결과를 병합합니다. - dcount_hll 함수를 사용하여 또는
hll_merge함수의 출력에서 고유 값의hll()수를 계산합니다.
Important
hll(), hll_if() 및 hll_merge()의 결과를 저장하고 나중에 검색할 수 있습니다. 예를 들어 일별 고유 사용자 요약을 만든 다음 주간 수를 계산하는 데 사용할 수 있습니다. 그러나 이러한 결과의 정확한 이진 표현은 시간이 지남에 따라 변경 될 수 있습니다. 이러한 함수가 동일한 입력에 대해 동일한 결과를 생성한다는 보장은 없으므로 이러한 함수를 사용하는 것이 좋습니다.
구문
hll(expr [, 정확도])
구문 규칙에 대해 자세히 알아봅니다.
매개 변수
| 이름 | Type | 필수 | 설명 |
|---|---|---|---|
| expr | string |
✔️ | 집계 계산에 사용되는 식입니다. |
| 정밀 | int |
속도와 정확도 사이의 균형을 제어하는 값입니다. 지정하지 않으면 기본값 1가 사용됩니다. 지원되는 값은 예측 정확도를 참조 하세요. |
반품
그룹 전체 expr의 고유 개수에 대한 중간 결과를 반환합니다.
예시
다음 예제에서는 함수를 hll() 사용하여 열의 각 10분 시간 bin 내에 있는 열의 DamageProperty 고유 값 수를 예측합니다 StartTime .
StormEvents
| summarize hll(DamageProperty) by bin(StartTime,10m)
표시된 결과 테이블에는 처음 10개의 행만 포함됩니다.
| StartTime | hll_DamageProperty |
|---|---|
| 2007-01-01T00:20:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T01:00:00Z | [[1024,14],["7755241107725382121","-5665157283053373866","3803688792395291579","-1003235211361077779"],[]] |
| 2007-01-01T02:00:00Z | [[1024,14],["-1003235211361077779","-5665157283053373866","7755241107725382121"],[]] |
| 2007-01-01T02:20:00Z | [[1024,14],["7755241107725382121"],[]] |
| 2007-01-01T03:30:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T03:40:00Z | [[1024,14],["-5665157283053373866"],[]] |
| 2007-01-01T04:30:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T05:30:00Z | [[1024,14],["3803688792395291579"],[]] |
| 2007-01-01T06:30:00Z | [[1024,14],["1589522558235929902"],[]] |
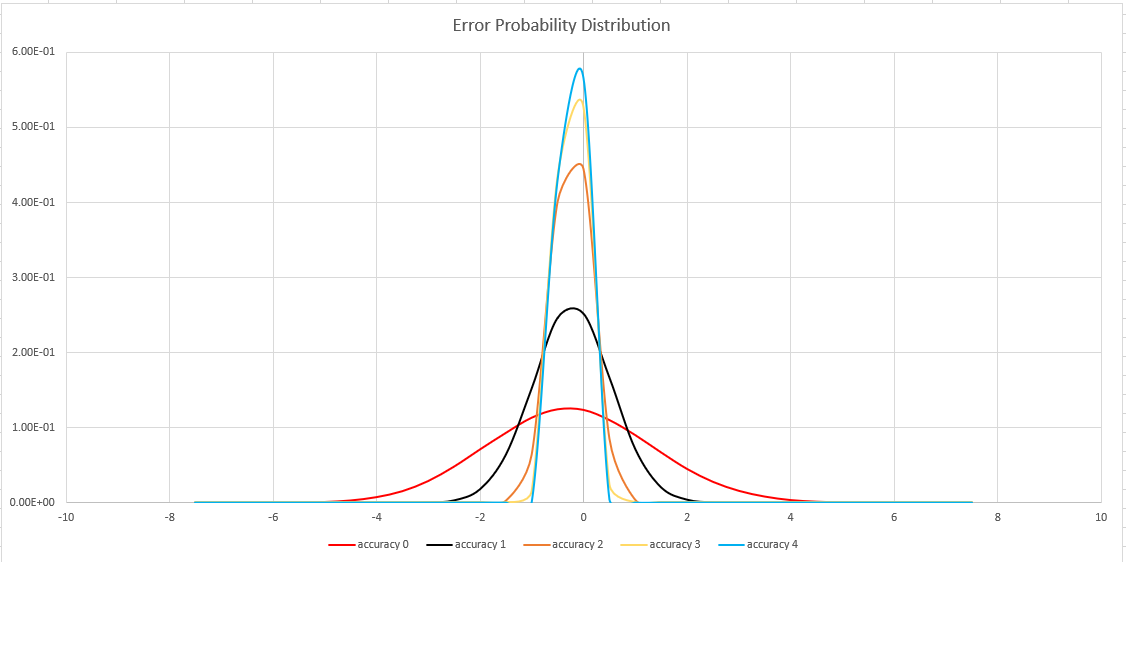
추정 정확도
이 함수는 집합 카디널리티의 확률적 추정을 수행하는 HLL(HyperLogLog) 알고리즘의 변형을 사용합니다. 알고리즘은 메모리 크기당 정확도 및 실행 시간의 균형을 맞추는 데 사용할 수 있는 "노브"를 제공합니다.
| 정확도(Accuracy) | 오류(%) | 항목 수 |
|---|---|---|
| 0 | 1.6 | 212 |
| 1 | 0.8 | 214 |
| 2 | 0.4 | 216 |
| 3 | 0.28 | 217 |
| 4 | 0.2 | 218 |
참고 항목
"항목 수" 열은 HLL 구현에서 1 바이트 카운터의 수입니다.
알고리즘에는 집합 카디널리티가 충분히 작은 경우 완벽한 개수(오류 0개)를 수행하기 위한 몇 가지 프로비저닝이 포함됩니다.
- 정확도 수준이
1이면 1000개의 값이 반환됩니다. - 정확도 수준이
2이면 8000개의 값이 반환됩니다.
바인딩된 오류는 이론적 바운드가 아닌 확률입니다. 값은 오류 분포의 표준 편차(시그마)이며 예측의 99.7%는 3 x 시그마 미만의 상대 오차를 갖습니다.
다음 이미지는 지원되는 모든 정확도 설정에 대한 상대 예측 오류의 확률 분포 함수를 백분율로 보여 줍니다.