PRT 수식(Direct3D 9)

PRT를 구현하는 셰이더를 완전히 이해하려면 셰이더가 종료 광도를 계산하는 데 사용하는 수식을 파생시키는 것이 유용합니다.

시작하려면 다음 수식은 임의의 먼 조명이 있는 확산 개체의 직접 조명으로 인한 출구 밝기를 계산하는 일반적인 수식입니다.

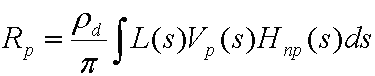있는 확산 개체의 직접 조명으로 인한 출구 광원의 수식입니다.

어디:

매개 변수	묘사
Rp	꼭짓점 p의 종료 광도입니다. 메시의 모든 꼭짓점에서 평가됩니다.
pd	표면의 알베도입니다.
원주율	에너지 절약 정규화 요인으로 사용되는 상수입니다.
L(s)	조명 환경(원본 밝기)입니다.
Vp₍s₎	지점 p에 대한 이진 표시 유형 함수입니다. 점이 빛을 볼 수 있으면 1이고, 그렇지 않으면 0입니다.
Hnp₍s₎	램버트의 법에서 코사인 용어. max((Np· s), 0과 같으며, 여기서 Np는 포인트 p의 표면 표준입니다.
s	구에 통합되는 변수입니다.

 

구형 조화와 같은 구형 기본 함수를 사용하여 다음 수식은 조명 환경을 근사화합니다.

조명 환경수식

어디:

매개 변수	묘사
L(s)	조명 환경(원본 밝기)입니다.
나는	기본 함수 수를 합산하는 정수입니다.
O	구형 하모닉의 순서입니다.
li	계수입니다.
Yi	구에 대한 몇 가지 기본 함수입니다.

 

이러한 계수 L'의 컬렉션은 기본 함수 Y와 함께 함수 L에 대한 최적 근사치를 제공합니다. 대체 및 분산은 다음 수식을 생성합니다.

l을 대체하고수식

Y_iVp₍s₎Hnp₍s₎의 정수는 시뮬레이터가 메시의 모든 꼭짓점에서 미리 계산하는 전송 계수 t_pi. 이 수식을 대체하면 다음 수식이 생성합니다.

전송 계수수식

이를 벡터 표기법으로 변경하면 다음과 같은 압축되지 않은 수식이 생성되어 각 채널의 종료 반경을 계산합니다.

벡터 표기법수식

어디:

매개 변수	묘사
Rp	꼭짓점 p의 종료 광도입니다.
pd	표면의 알베도입니다.
L'	li벡터이며, 구형 조화 기반 함수에 소스 광채를 투영하는 것입니다. 구형 조화 계수의 order² 벡터입니다.
휴지	꼭짓점 p에 대한 order² 전송 벡터입니다. 시뮬레이터는 전송 계수를 p로 나눕니다.

 

이러한 두 벡터는 구형 조화 계수의 order² 벡터이므로 단순히 점 제품입니다. 순서에 따라 점의 비용이 많이 들 수 있으므로 압축을 사용할 수 있습니다. CPCA(클러스터형 보안 주체 구성 요소 분석)라는 알고리즘은 데이터를 효율적으로 압축합니다. 이렇게 하면 더 높은 순서의 구면 고조파 근사치를 사용하여 더 선명한 그림자를 생성할 수 있습니다.

CPCA는 전송 벡터를 근사값으로 계산하는 다음 수식을 제공합니다.

근사치 전송 벡터수식

어디:

매개 변수	묘사
휴지	꼭짓점 p의 전송 벡터입니다.
Mk	클러스터 k의 평균입니다.
j	PCA 벡터 수를 합산하는 정수입니다.
N	PCA 벡터 수입니다.
wpj	포인트 p의 jth PCA 가중치입니다.
Bkj	클러스터 k에 대한 jth PCA 기본 벡터입니다.

 

클러스터는 동일한 평균 벡터를 공유하는 몇 가지 꼭짓점입니다. 클러스터 평균, PCA 가중치, PCA 기본 벡터 및 꼭짓점의 클러스터 ID를 가져오는 방법은 다음과 같습니다.

이러한 두 수식을 대체하면 다음이 생성됩니다.

전송 벡터.

그런 다음 점 제품을 배포하면 다음 수식이 생성됩니다.

점 제품수식

왜냐하면 둘 다(Mk· L') 및 (B_kj· L')은 꼭짓점당 상수이며, 샘플은 CPU를 사용하여 이러한 값을 계산하고 꼭짓점 셰이더에 상수로 전달합니다. w_pj 각 꼭짓점에 대한 변경 내용이므로 이 샘플은 꼭짓점별 데이터를 꼭짓점 버퍼에 저장합니다.

관련 항목

사전 계산된 래디언스 전송